• Inicio
• Fenómenos de transporte
• Difusión unidimensional

Difusión. Ley de Fick

La experiencia nos demuestra que cuando abrimos un frasco de perfume o de cualquier otro líquido volátil, podemos olerlo rápidamente en un recinto cerrado. Decimos que las moléculas del líquido después de evaporarse se difunden por el aire, distribuyéndose en todo el espacio circundante. Lo mismo ocurre si colocamos un terrón de azúcar en un vaso de agua, las moléculas de sacarosa se difunden por todo el agua. Estos y otros ejemplos nos muestran que para que tenga lugar el fenómeno de la difusión, la distribución espacial de moléculas no debe ser homogénea, debe existir una diferencia, o gradiente de concentración entre dos puntos del medio.

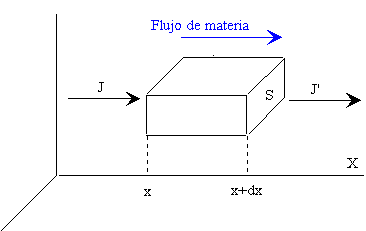
Supongamos que su concentración varía con la posición al lo largo del eje X. Llamemos J a la densidad de corriente de partículas, es decir, al número efectivo de partículas que atraviesan en la unidad de tiempo un área unitaria perpendicular a la dirección en la que tiene lugar la difusión. La ley de Fick afirma que la densidad de corriente de partículas es proporcional al gradiente de concentración

${\displaystyle J=-D\frac{\partial n}{\partial x}}$

La constante de proporcionalidad se denomina coeficiente de difusión D y es característico tanto del soluto como del medio en el que se disuelve.

La acumulación de partículas en la unidad de tiempo que se produce en el elemento de volumen S·dx es igual a la diferencia entre el flujo entrante JS, menos el flujo saliente J’S, es decir

${\displaystyle JS-J\text{'}S=\frac{\partial J}{\partial x}Sdx}$

La acumulación de partículas en la unidad de tiempo es

${\displaystyle (Sdx)\frac{\partial n}{\partial t}}$

Igualando ambas expresiones y utilizando la Ley de Fick se obtiene

${\displaystyle \frac{\partial }{\partial x}\left(D\frac{\partial n}{\partial x}\right)=\frac{\partial n}{\partial t}}$

Ecuación diferencial en derivadas parciales que describe el fenómeno de la difusión . Si el coeficiente de difusión D no depende de la concentración

${\displaystyle \frac{1}{D}\frac{\partial n}{\partial t}=\frac{{\partial }^{2}n}{\partial x^2}}$

Difusión unidimensional

Vamos a considerar el problema de la difusión unidimensional de una masa M de soluto, situada en el origen de un medio unidimesional representado por el eje X.

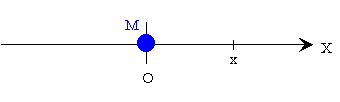
La solución de la ecuación diferencial nos da la concentración en los puntos x del medio en cada instante de tiempo t.

${\displaystyle n(x,t)=\frac{M}{2\sqrt{\pi Dt}}\exp \left(\frac{-x^2}{4Dt}\right)}$

La cual se puede comprobarse por simple sustitución en la ecuación diferencial

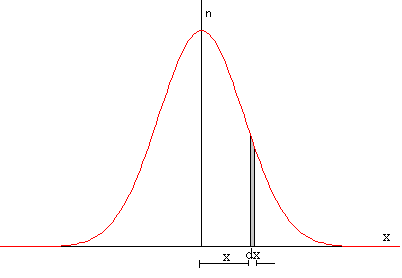
En el programa interactivo, cada vez que se introduce el valor del tiempo, se traza en la ventana del applet la función n(x,t). Se puede observar que el área bajo la curva acampanada es la misma para todos las gráficas. Como puede comprobarse

${\displaystyle {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}n(x,t)dx}=2{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{M}{2\sqrt{\pi Dt}}\exp \left(\frac{-x^2}{4Dt}\right)}dx=M}$

Para ello, se emplea el resultado de la integral

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-\alpha x^2)dx}=\frac{1}{2}\sqrt{\frac{\pi }{\alpha }}}$

Desplazamiento medio cuadrático

${\displaystyle <x^2>=\frac{1}{M}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{x}^2}n(x,t)dx=\frac{1}{\sqrt{\pi Dt}}{\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^2\exp \left(\frac{-x^2}{4Dt}\right)}dx}$

Integramos por partes

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^2\exp (-\alpha x^2)dx}=\frac{1}{2\alpha }\left({-x\exp (-\alpha x^2)|}_0^{\infty }+{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp (-\alpha x^2)dx}\right)=\frac{1}{4\alpha }\sqrt{\frac{\pi }{\alpha }}\\ <x^2>=\frac{1}{\sqrt{\pi Dt}}{\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^2\exp \left(\frac{-x^2}{4Dt}\right)}dx=2Dt\end{array}}$

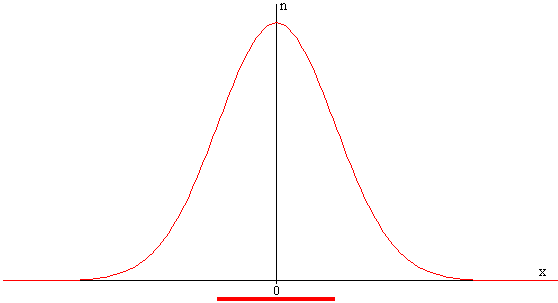
Debajo de cada curva, se traza un segmento cuya longitud es igual al doble de la raíz cuadrada de la media de los cuadrados de los desplazamientos de las partículas y mide la extensión efectiva de las partículas en el medio.

${\displaystyle \sqrt{<x^2>}=\sqrt{2Dt}}$

Vamos a estudiar dos tipos de difusión

1. Gas en aire, se supondrán gases ideales. En esta aproximación, el coeficiente de difusión se mantiene constante y no varía con la concentración.

2. De un soluto sólido en un disolvente, el coeficiente de difusión es sensible a la concentración, aunque supondremos disoluciones diluidas. Para bajas concentraciones, el coeficiente de difusión se mantiene aproximadamente constante.

En los dos ejemplos de difusión, de un gas en aire, o de un soluto en agua (líquido), se pone de manifiesto la relación entre el orden de magnitud del coeficiente de difusión y la escala de longitud o de tiempo en el que transcurren ambos fenómenos.

Actividades

• Se elige el soluto y el disolvente.  Se presentan dos grupos: gases y vapores en aire en el que el exponente del coeficiente de difusión es -4, y soluciones acuosas en el que el exponente del coeficiente de difusión es -9.

Gases y vapores en aire
1	Hidrógeno	0.64 10-4
2	Oxígeno	0.18 10-4
3	Alcohol	0.10 10-4
4	Benceno	0.08 10-4
Soluciones acuosas
5	Azúcar	0.36 10-9
6	Sal común	1.10 10-9
7	Alcohol	0.80 10-9

• El instante t, en horas (Gases y vapores) o en días (Soluciones acuosas), en el que deseamos representar la distribución de concentraciones n(x, t) de cada punto x del medio unidimensional, en el control de edición o actuando en la barra de desplazamiento titulada Tiempo.

Se pulsa en el botón titulado Gráfica.

Se representa la concentración n(x, t) de cada punto x del medio unidimensional en el instante actual (en color rojo) y en el instante previamente introducido (en color azul).

Cuestiones

Debajo de la curva se traza un segmento que mide la extensión efectiva de las partículas de soluto en el disolvente. En la parte superior derecha, se proporciona el valor numérico de la longitud de dicho segmento.

Comparar la difusión en dos casos pertenecientes al mismo grupo, midiendo la extensión efectiva de soluto en el disolvente en los mismos instantes.

Comparar la difusión de un gas en aire y de una solución acuosa, midiendo la extensión efectiva de soluto en el disolvente en los mismos instantes. Las unidades de medida del eje X están marcadas en dm.

DifusionApplet3 aparacerá en un explorador compatible con JDK 1.1

Referencias

Puig Adam P., Curso teórico-práctico de ecuaciones diferencias aplicado a la Física y Técnica. Biblioteca Matemática (1970), págs. 305

Puig Adam P.,  Curso teórico-práctico de cálculo integral aplicado a la Física y Técnica. Biblioteca Matemática (1972), págs. 124-125

Curso Interactivo de Física en Internet © Ángel Franco García