Diagonalización de matrices

1. Dada la matriz

${\displaystyle A=\left(\begin{array}{ccc}-1& 0& -3\\ 3& 2& 3\\ -3& 0& -1\end{array}\right)}$

¿Es diagonalizable?. En caso afirmativo calcular la base tal que la matriz asociada es diagonal y hallar la relación entre la matriz diagonal y la dada A.

>> syms v
>> A=sym('[-1-v,0,-3;3,2-v,3;-3,0,-1-v]')
A = 
[ - v - 1,     0,      -3]
[       3, 2 - v,       3]
[      -3,     0, - v - 1]
>> solve(det(A))
ans =
  2
  2
 -4
>> A1=sym('[-3,0,-3;3,0,3;-3,0,-3]')
A1 =
 [ -3, 0, -3]
[  3, 0,  3]
[ -3, 0, -3]

Ker(f-2e)={(x,y,-x)}, dos vectores propios (1,0,-1),(0,1,0)

>> A2=sym('[3,0,-3;3,6,3;-3,0,3]') 
A2 =
[  3, 0, -3]
[  3, 6,  3]
[ -3, 0,  3]
>> syms x y z
>> [x y]=solve('x-z','x+2*y+z')
x = z
y = -z

Ker(f+4e)={(x,-x,x)}, dos vectores propios (1,-1,1)

2. Relación entre la matriz diagonal y la dada, D=P^-1AP

>> A=sym('[-1,0,-3;3,2,3;-3,0,-1]')
A =
[ -1, 0, -3]
[  3, 2,  3]
[ -3, 0, -1]
>> P=sym('[1,0,1;0,1,-1;-1,0,1]')
P =
[  1, 0,  1]
[  0, 1, -1]
[ -1, 0,  1]
>> D=P\A*P
D =
[ 2, 0,  0]
[ 0, 2,  0]
[ 0, 0, -4]

Con la función eig

>> A=sym('[-1,0,-3;3,2,3;-3,0,-1]')
 
A =
[ -1, 0, -3]
[  3, 2,  3]
[ -3, 0, -1]
>> [V D]=eig(A)
V =
[  1, 0, -1]
[ -1, 1,  0]
[  1, 0,  1]
D =
[ -4, 0, 0]
[  0, 2, 0]
[  0, 0, 2]
>> V\A*V
ans =
[ -4, 0, 0]
[  0, 2, 0]
[  0, 0, 2]

3. Estudiar para qué valores de a y b es diagonizable la matriz

${\displaystyle A=\left(\begin{array}{ccc}a+2& b& 0\\ 3& 2& -3\\ 2& b& a\end{array}\right)}$

>> syms a b v
>> A=sym('[a+2-v,b,0;3,2-v,-3;2,b,a-v]')
A =
[ a - v + 2,     b,     0]
[         3, 2 - v,    -3]
[         2,     b, a - v]
>> solve(det(A))
ans =
     2
     a
 a + 2

1. Primer caso, a=2, valor propio doble

>> A=sym('[2,b,0;3,0,-3;2,b,0]')
A =
[ 2, b,  0]
[ 3, 0, -3]
[ 2, b,  0]
>> rank(A)
ans =2

no depende de b, NO DIAGONALIZABLE

2. Segundo caso, a=0. El valor propio 2 es doble

>> A=sym('[0,b,0;3,0,-3;2,b,-2]')
A = 
[ 0, b,  0]
[ 3, 0, -3]
[ 2, b, -2]

Será diagonalizable si b=0

3. Tercer caso, a≠0,2

Los valores propios son distintos, es DIAGONALIZABLE

Con la función eig

>> syms a b
>> A=sym('[a+2,b,0;3,2,-3;2,b,a]')
A =
[ a + 2, b,  0]
[     3, 2, -3]
[     2, b,  a]
>> [V D]=eig(A)
V =
[    1, 1, (3*b)/(2*(a + (3*b)/2 - 2))]
[ -a/b, 0,        -3/(a + (3*b)/2 - 2)]
[    1, 1,                           1]
D =
[ 2,     0, 0]
[ 0, a + 2, 0]
[ 0,     0, a]

Si a=0, NO DIAGONALIZABLE (1° vector columna=2° vector columna)

Si a=2, NO DIAGONALIZABLE (1° vector columna=3° vector columna)

4. Dada la matriz

${\displaystyle A=\left(\begin{array}{ccc}7& -2& 1\\ -2& 10& -2\\ 1& -2& 7\end{array}\right)}$

¿Es diagonalizable?. En caso afirmativo calcular la base tal que la matriz asociada es diagonal y hallar la relación entre la matriz diagonal y la dada A.

>> A=sym('[7,-2,1;-2,10,-2;1,-2,7]')
A =
[  7, -2,  1]
[ -2, 10, -2]
[  1, -2,  7]
>> [V D]=eig(A)
V =
[  1, 2, -1]
[ -2, 1,  0]
[  1, 0,  1]
D =
[ 12, 0, 0]
[  0, 6, 0]
[  0, 0, 6]
>> V\A*V
ans =
[ 12, 0, 0]
[  0, 6, 0]
[  0, 0, 6]

5. Estudiar para qué valores del parámetro a, es diagonizable la matriz

${\displaystyle A=\left(\begin{array}{ccc}1& a-1& 1\\ 0& a& 1\\ 1& 0& a\end{array}\right)}$

>> syms a v
>> A=sym('[1-v,a-1,1;0,a-v,1;1,0,a-v]')
A =
[ 1 - v, a - 1,     1]
[     0, a - v,     1]
[     1,     0, a - v]
>> solve(det(A))
ans =
     1
 a + 1
 a - 1

1. Primer caso, a≠0,2

Los tres valores son distintos, DIAGONALIZABLE

2. Segundo caso, a=0. Un valor propio doble

>> A=sym('[0,-1,1;0,-1,1;1,0,-1]')
A =
[ 0, -1,  1]
[ 0, -1,  1]
[ 1,  0, -1]
>> rank(A)
ans = 2 

NO DIAGONALIZABLE

3. Tercer caso, a=2. Un valor propio doble

>> A=sym('[0,1,1;0,1,1;1,0,1]')
A =
[ 0, 1, 1]
[ 0, 1, 1]
[ 1, 0, 1]
>> rank(A)
ans =2

Tampoco es DIAGONALIZABLE

>> A=sym('[1,a-1,1;0,a,1;1,0,a]')
A =
 
[ 1, a - 1, 1]
[ 0,     a, 1]
[ 1,     0, a]
>> [V D]=eig(A)
V =
[      1 - a, 1, -1]
[ -1/(a - 1), 1, -1]
[          1, 1,  1]
D =
[ 1,     0,     0]
[ 0, a + 1,     0]
[ 0,     0, a - 1]

Para a=0, 1ª columna =2ª columna, NO DIAGONALIZABLE

Para a=2, 1ª columna =3ª columna, NO DIAGONALIZABLE

6. Estudiar para qué valores de a y b, es diagonizable la matriz

${\displaystyle \left(\begin{array}{ccc}a& 1& 1\\ a& 1& 2b\\ 0& 0& 2\end{array}\right)}$

Hallando los valores propios:

${\displaystyle \left|\begin{array}{ccc}a-\lambda & 1& 1\\ a& 1-\lambda & 2b\\ 0& 0& 2-\lambda \end{array}\right|=(2-\lambda )({\lambda }^2-a\lambda -\lambda ))=\lambda (2-\lambda )(\lambda -a-1)}$

Valores propios: λ=0, λ=2, λ=a+1

1. Caso: a≠-1 y 1, los valores propios son simples⇒Diagonalizable

2. Caso: a=-1⇒λ=0, es doble

${\displaystyle r\left(\begin{array}{ccc}-1& 1& 1\\ -1& 1& 2b\\ 0& 0& 2\end{array}\right)=2}$

no depende de b⇒ dim(ker(f))=1≠2, No diagonizable

3. Caso: a=1⇒λ=2, es doble

${\displaystyle r\left(\begin{array}{ccc}-1& 1& 1\\ 1& -1& 2b\\ 0& 0& 0\end{array}\right)=\{\begin{array}{l}2,b\ne \frac{-1}{2}\Rightarrow \text{No diagonalizable}.\\ 1,b=\frac{-1}{2}\Rightarrow \text{diagonalizable}.\end{array}}$

>> syms a b v
>> A=sym('[a-v,1,1;a,1-v,2*b;0,0,2-v]')
A = 
[ a - v,     1,     1]
[     a, 1 - v,   2*b]
[     0,     0, 2 - v]
>> solve(det(A))
ans = 
     0
     2
 a + 1

1. Caso a≠-1, 1 valores propios distintos, DIAGONALIZABLE

2. Caso a=1, 0 valor propio doble

>> A=sym('[-1,1,1;-1,1,2*b;0,0,2]')
A =
[ -1, 1,   1]
[ -1, 1, 2*b]
[  0, 0,   2]
>> A=sym('[-1,1,1;-1,1,2*b;0,0,2]')
A =
[ -1, 1,   1]
[ -1, 1, 2*b]
[  0, 0,   2]
>> rank(A)
ans = 2

NO DIAGONALIZABLE

3. Caso a=1, 2 valor propio doble

A =
[ -1,  1,   1]
[  1, -1, 2*b]
[  0,  0,   0]

Es diagonalizable si b=-1/2

>> A=sym('[a,1,1;a,1,2*b;0,0,2]')
A = 
[ a, 1,   1]
[ a, 1, 2*b]
[ 0, 0,   2] 
>> [V D]=eig(A) 
V = 
[ -1/a,         -(b + 1/2)/(a - 1), 1]
[    1, -(a/2 + 2*b - a*b)/(a - 1), 1]
[    0,                          1, 0]  
D = 
[ 0, 0,     0]
[ 0, 2,     0]
[ 0, 0, a + 1]

Si a=-1, 1ª columna =3ª columna, NO DIAGONALIZABLE

Rectas y planos

1. Sea r la recta de ecuaciones implícitas:

${\displaystyle r\equiv \{\begin{array}{l}2x+y+z=0\\ x+y-z=0\end{array}}$

Hallar las ecuaciones en forma continua y paramétrica

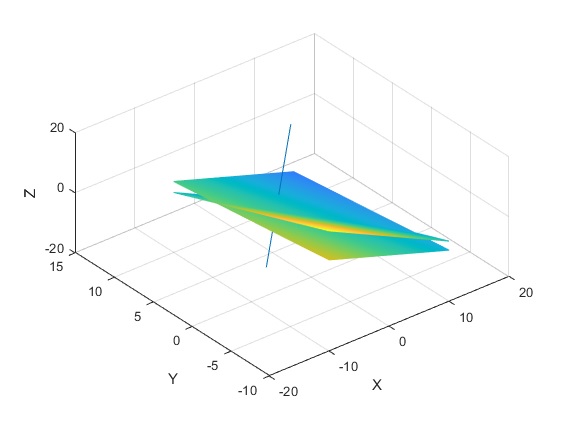
>> [x y]=meshgrid(-4:0.1:4);
>> z=-2*x-y;
>> mesh(x,y,z)
>> grid on
>> hold on
>> z=x+y;
>> mesh(x,y,z)
>> hold off



${\displaystyle \begin{array}{l}y+z=-2x\\ y-z=-x\end{array}\}\Rightarrow \{\begin{array}{l}x=x\\ y=-\frac{3}{2}x\\ z=-\frac{x}{2}\end{array}\frac{x}{2}=\frac{y}{-3}=\frac{z}{-1}}$

Quitando el hold off y añadiendo

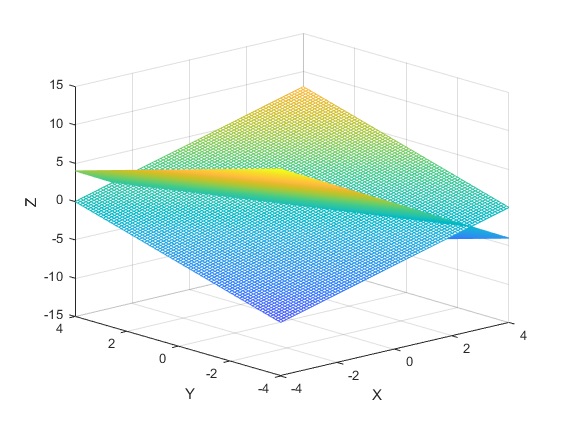
>> x=-4:0.1:4;
>> y=-3*x/2;
>> z=-x/2;
>> plot3(x,y,z)
>> hold off



2. Intersección de recta $\{\begin{array}{l}x=1+t\\ y=1+2t\\ z=-1-t\end{array}$ y plano, z=x+y-3

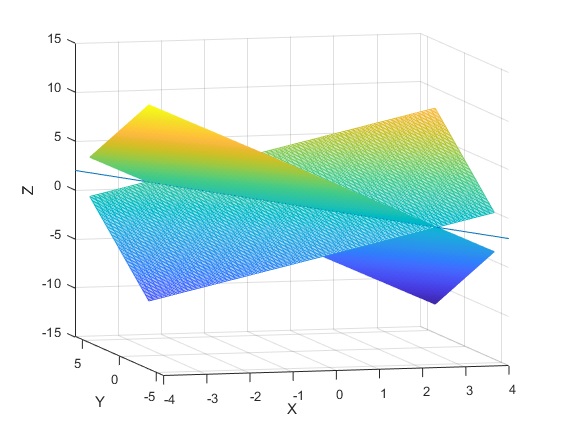
>> [x y]=meshgrid(-4:0.1:4);
>> z=x+y-3;
>> mesh(x,y,z)
>> grid on 
>> hold on
>> t=-7:0.1:5;
>> x=1+t;
>> y=1+2*t;
>> z=-1-t;
>> plot3(x,y,z)
>> hold off



3. Intersección de tres planos: z=(31-2x-6y)/3, z=(10-7x+5y)/5, z=3x-17y+52

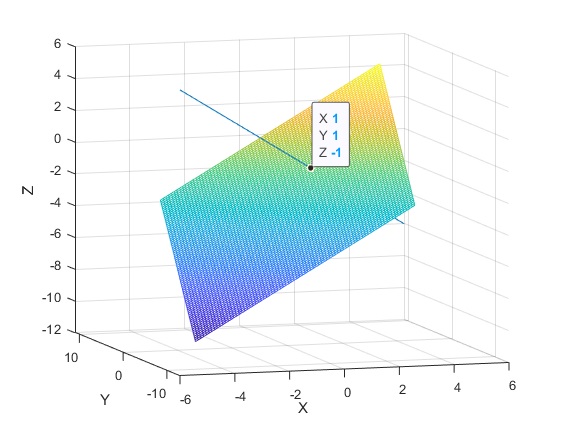
>> A=sym('[2, 6, 3;7, -5, 5;3, -17, -1]')
A =
[ 2,   6,  3]
[ 7,  -5,  5]
[ 3, -17, -1]
>> det(A)
ans = 0
>> B=sym('[2, 6, 31;7, -5, 10;3, -17, -52]')
B =
[ 2,   6,  31]
[ 7,  -5,  10]
[ 3, -17, -52]
>> det(B) 
ans = 0

Representación gráfica

>> [x y]=meshgrid(-5:0.1:5);
z=(31-2*x-6*y)/3;
hold on 
grid on
mesh(x,y,z)
z=(10-7*x+5*y)/5;
mesh(x,y,z)
z=3*x-17*y+52;
mesh(x,y,z)
hold off



4. Intersección de recta y=x/2, z=0 y plano z=(-1-x+y)/2

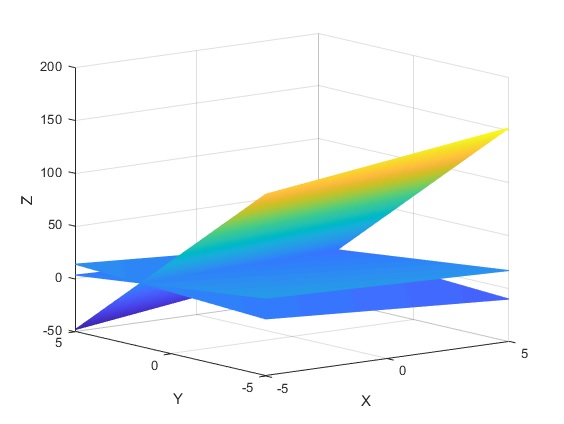
A =
[ 1, -1, 2]
[ 1, -2, 0]
[ 0,  0, 1]
>> det(A)
 ans = -1

Representación gráfica

>> [x y]=meshgrid(-5:0.1:5);
hold on
grid on
z=(-1-x+y)/2;
mesh(x,y,z)
>> x=-5:0.1:5;
>> y=x/2;
z=0*x;
plot3(x,y,z)
>> hold off



5. Intersección de recta $\{\begin{array}{l}x=1+3t\\ y=5+2t\\ z=-2-t\end{array}$ y los planos z=-x-y, z=(1-2x-y)/3

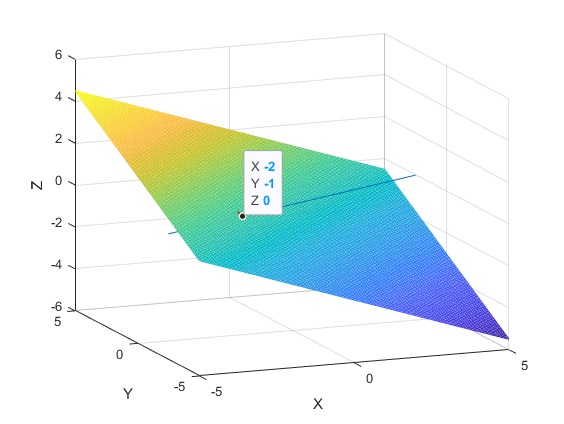
>> [x y]=meshgrid(-10:0.1:10);
>> hold on
grid on
z=-x-y;
mesh(x,y,z)
z=(1-2*x-y)/3;
mesh(x,y,z)
t=-5:0.1:5;
x=1+3*t;
y=5+2*t;
z=-2-t;
plot3(x,y,z)
hold off