Raíces de una ecuación
La ecuación de segundo grado
Creamos el script
a=input('primer coeficiente');
b=input('segundo coeficiente');
c=input('tercer coeficiente');
x1=(-b+sqrt(b^2-4*a*c))/(2*a);
x2=(-b-sqrt(b^2-4*a*c))/(2*a);
disp([x1 x2])
disp(x1)
disp(x2)
Lo guardamos con el nombre
-
Ejemplo 1: x2+4x+6=0
>> ecuacion primer coeficiente: 1 segundo coeficiente: 4 tercer coeficiente: 6 -2.0000 + 1.4142i -2.0000 - 1.4142i -2.0000 + 1.4142i -2.0000 - 1.4142i
Ejemplo 2: x2-2x-3=0
>> ecuacion
primer coeficiente: 1
segundo coeficiente: -2
tercer coeficiente: -3
3 -1
3
-1
También podemos crear una función:
function [x1,x2] = ecuacion_segundo(a,b,c)
x1=(-b+sqrt(b^2-4*a*c))/(2*a);
x2=(-b-sqrt(b^2-4*a*c))/(2*a);
end
Lo guardamos con el nombre
[z1 z2]=ecuacion_segundo(1,4,6)
z1 = -2.0000 + 1.4142i
z2 = -2.0000 - 1.4142i
>> [v1 v2]=ecuacion_segundo(1,-2,-3)
v1 = 3
v2 = -1
Ecuaciones de grado 'n'
Se emplea la función
>> x=roots(p)
-
Ejemplo 1: x4+x3-13x+8=0
>> p=[1,4,0,-13,8];
>> x=roots(p)
x = -2.9096 + 1.1406i
-2.9096 - 1.1406i
1.0000
0.8191
Asociada a la función
Aplicamos la función poly a un vector que contenga las raíces de la ecuación, nos devuelve los coeficientes de dicha ecuación.
Ejemplo 2: x5+5x4-3x3-15x2-4x-20=0
>> p=[1 5 -3 -15 -4 -20];
>> x=roots(p)
x =-5.0000
2.0000
-2.0000
0.0000 + 1.0000i
0.0000 - 1.0000i
Ahora aplicando la función
>> q=[-5 2 -2 i -i];
>> c=poly(q)
c = 1 5 -3 -15 -4 -20
NOTA: con
>> a=[1i -1i];
>> poly(a)
ans = 1 0 1
La función
Ejemplo: f(x)=x5+5x4-3x3-15x2-4x-20 , si queremos hallar f(11)
>> p=[1 5 -3 -15 -4 -20];
>> polyval(p,11)
ans = 228384
>> polyval(p,0)
ans = -20
Esto nos permitirá conocer si ciertos valores son raíces o no de la ecuación. Comprobando con el ejercicio anterior:
>> polyval(p,-5)
ans = 0
>> polyval(p,i)
ans = 0
>> polyval(p,-i)
ans = 0
>> polyval(p,-2)
ans = 0
>> polyval(p,2)
ans = 0
Raíces, utilizando
>> syms x;
solve(x^3+6*x^2+11*x+6,x)
ans = -3,-2,-1
Comprobamos con
>> p=[1 6 11 6];
>> roots(p)
ans = -3.000
-2.0000
-1.0000
Ejemplo:
>> a=[1 1 1];
>> roots(a)
ans = -0.5000 + 0.8660i
-0.5000 - 0.8660i
>> solve(x^2+x+1,x)
ans = - 1/2 + (3^(1/2)*i)/2
- 1/2 - (3^(1/2)*i)/2
>> double(ans)
ans = -0.5000 - 0.8660i
-0.5000 + 0.8660i
En vez de
Ejercicios
Hallar las raíces de las siguientes ecuaciones:
En las dos primeras, comprobar que los valores obtenidos son las soluciones de las ecuaciones.
Si la gráfica de función y=f(x) corta al eje OX en los puntos x=-4,1,3 y 7. Calcular f(21).
Ecuaciones transcendentes
En la ingeniería a menudo nos encontramos con ecuaciones que no se pueden resolver por los métodos analíticos, para estos casos intentaremos obtener una solución aproximada.
El teorema de Bolzano, que nos permitirá localizar las soluciones afirma que si una función y=f(x) es continua en un intervalo cerrado [a, b] y toma valores de signo opuesto en los extremos del mismo, dicha función se anula, por lo menos en un punto interior.
En este apartado trabajaremos con funciones anónimas que nos permiten definir una función sin necesidad de guardarla en un fichero .m. Ejemplos
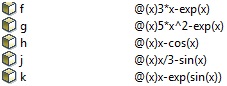
>> f=@(x) 3*x-exp(x); >> g=@(x) 5*x^2-exp(x); >> h=@(x) x-cos(x); >> j=@(x) x/3-sin(x); >> k=@(x) x-exp(sin(x));
En el Workspace aparecen con el siguiente símbolo
Método gráfico
Tenemos la ecuación : 3x-ex=0.
y=f(x)=3x-ex es continua en todo R
-
f(0)<0, f(1)>0, aplicando Bolzano una solución estará en el intervalo [0,1]
-
f(1)>0, f(2)<0, la otra solución estará en el intervalo [1,2]
>> f(0)
ans = -1
>> f(1)
ans = 0.2817
>> f(2)
ans = -1.3891
Con
>> f=@(x)3*x-exp(x); >> fplot(f,[0 2]) >> grid on
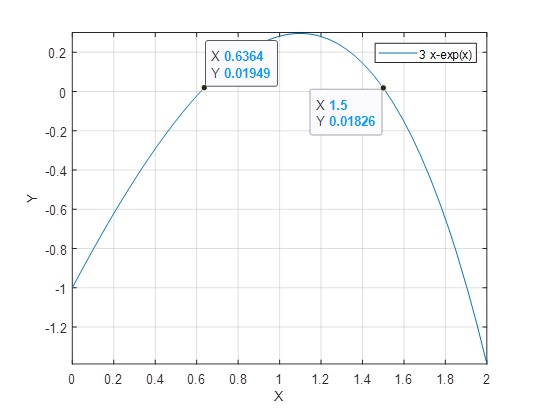
Nos acercamos a la primera raíz
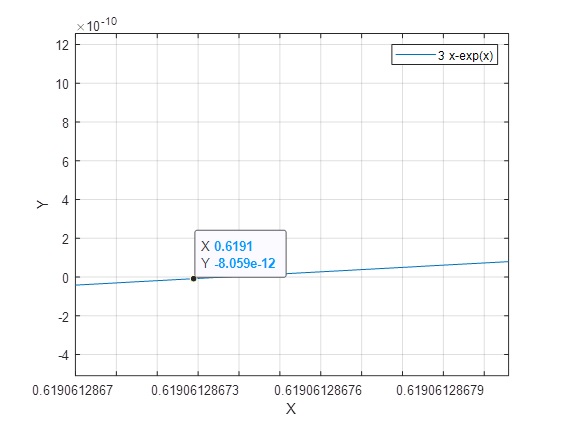
>> [x y]=ginput
x = 0.6191
y = -1.2062e-11
Con la otra raíz:
>> [x y]=ginput
x = 1.5121
y = -5.3180e-13
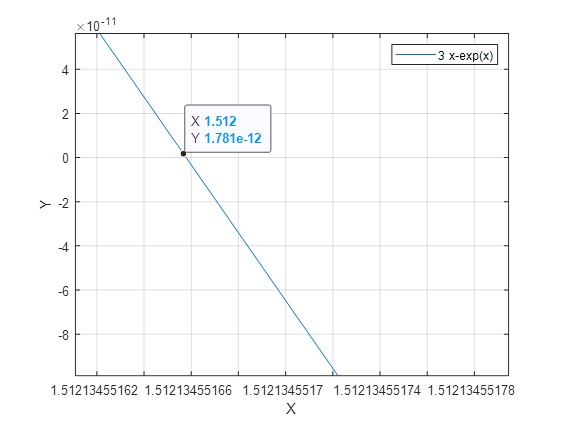
De otra forma: Intersección
>> n=@(x)exp(x); >> fplot(n,[0 2]) >> grid on >> hold on >> m=@(x) 3*x; >> fplot(m,[0 2]) >> hold off
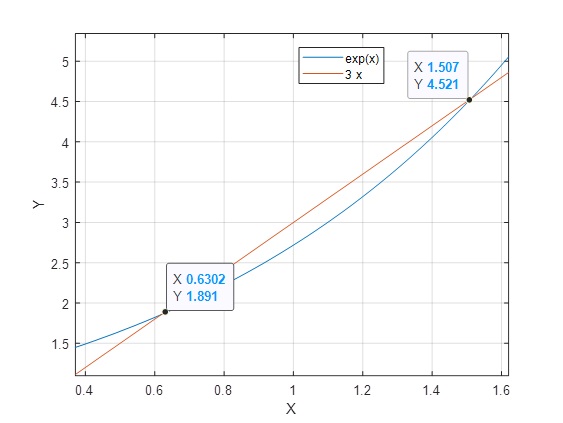
Nos acercamos a la primera intersección
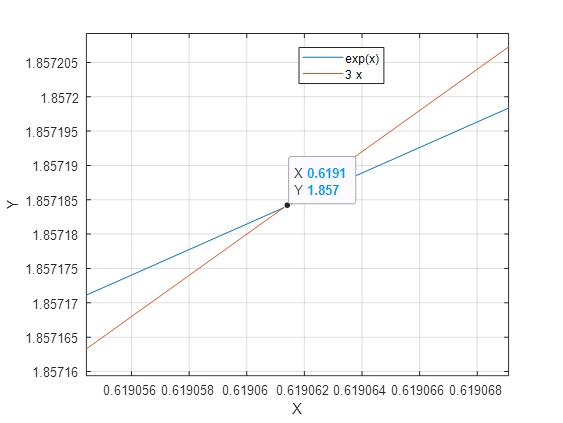
>> [x,y]=ginput
x = 0.6191
y = 1.8572
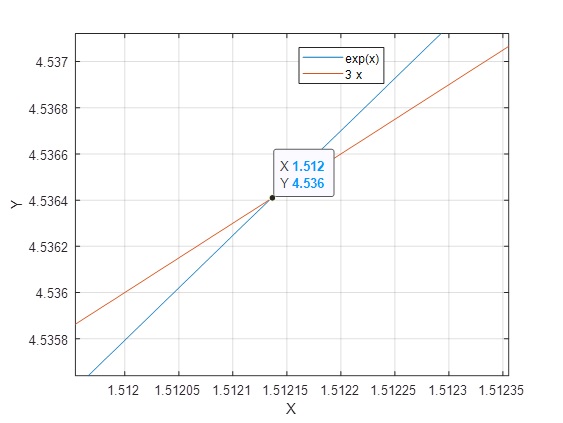
>> [x,y]=ginput
x = 1.5121
y = 4.5364
Ahora utilizando la función
>> fzero(f,[0 1])
ans = 0.6191
>> fzero(f,[1 2])
ans = 1.5121
Nota.- La función
Ejemplos
Ejemplo 1: 5x2-ex
>> g(-1)
ans = 4.6321
>> g(0)
ans = -1
Hay una solución en [-1 0].
>> g(4)
ans = 25.4018
>> g(5)
ans = -23.4132
Hay una solución en [4 5].
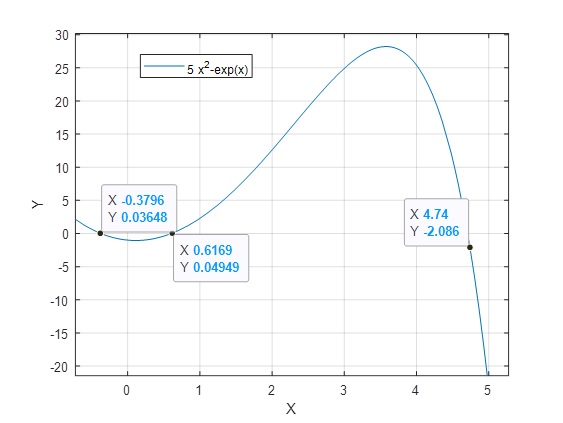
Nos acercamos a la primera raíz
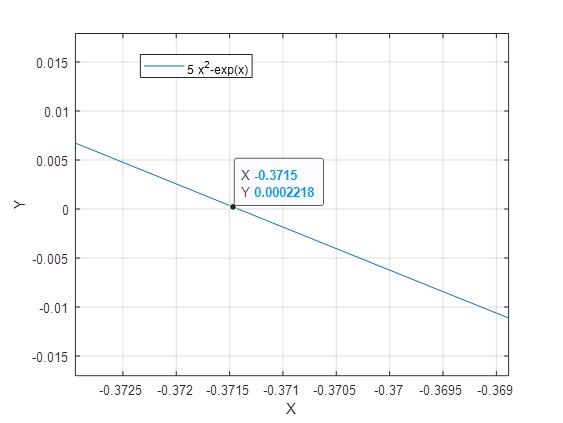
>> [x,y]=ginput
x = -0.3715
y = 2.4567e-04
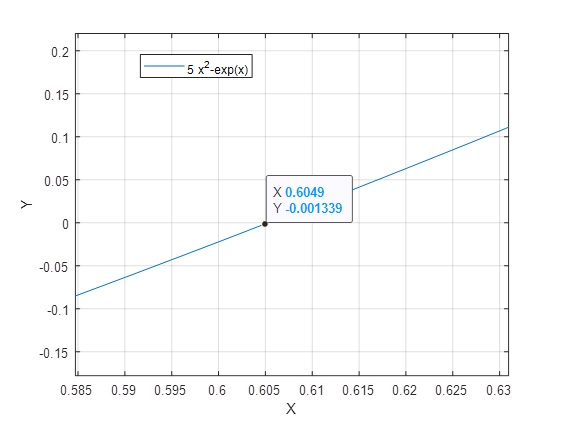
>> [x,y]=ginput
x = 0.6051
y = -9.1575e-04
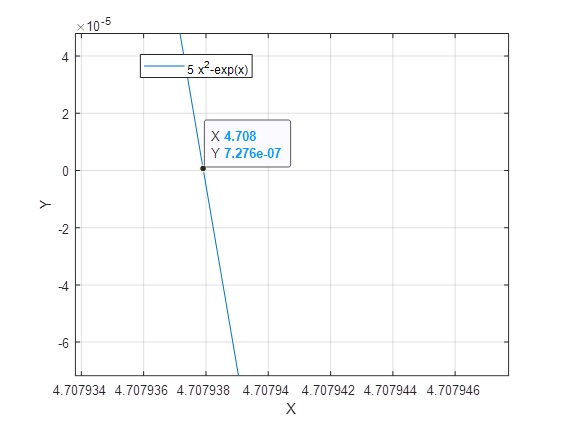
>> [x,y]=ginput
x = 4.7079
y = 6.2443e-07
Como intersección:
>> n=@(x)exp(x); >> m=@(x) 5*x.^2; >> fplot(n,[-1 5]) >> grid on >> hold on >> fplot(m,[-1 5]) >> hold off
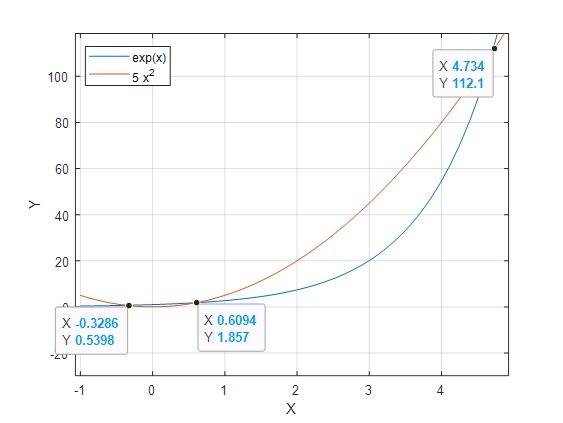
Ahora con la función
>> fzero(g,[-1 0])
ans = -0.3714
>> fzero(g,[0 1])
ans = 0.6053
>> fzero(g,[4 5])
ans = 4.7079
Ejemplo 2: x-cosx=0
>> j=@(x) x-cos(x); >> fplot(j,[-1.5 1.5]) >> grid on
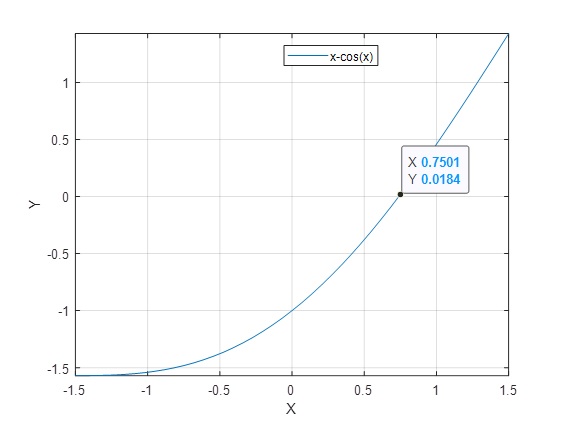
Como intersección:
>> m=@(x)cos(x); >> n=@(x) x; >> grid on >> hold on >> fplot(n,[-5 5]) >> fplot(m,[-5 5]) >> hold off
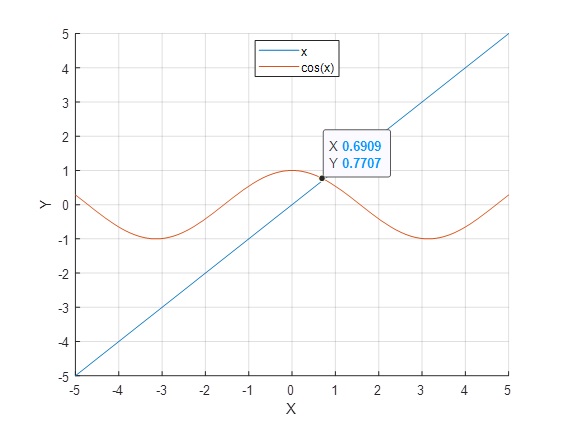
>> fzero(j,[-1 1])
ans = 0.7391
Ejemplo 3: x/3-sen(x)=0;
>> f=@(x) x/3-sin(x); %'f' es una función impar. >> fplot(f,[-15 15]) >> grid on
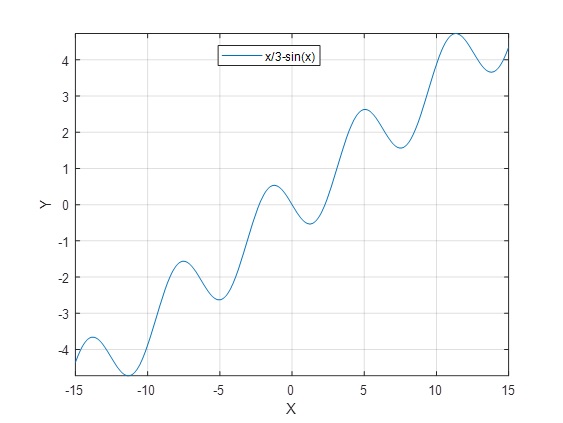
Nos acercamos a las raíces como en los ejercicios anteriores y obtener su valor con más aproximación.
>> m=@(x) x/3; >> n=@(x) sin(x); >> fplot(m,[-4 4]) >> grid on >> hold on >> fplot(n,[-4 4]) >> hold off
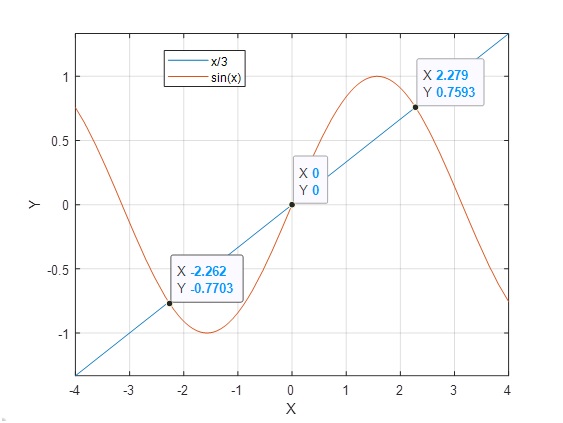
>> fzero(f,[-3 -1])
ans = -2.2789
>> fzero(f,[-1 1])
ans = 0
>> fzero(f,[1 3])
ans = 2.2789
Ejemplo 4: x-esen(x)=0
>> g=@(x) x-exp(sin(x));
>> g(2)
ans = -0.4826
>> g(3)
ans = 1.8484
Tiene una raíz en [2,3].
>> fplot(g,[-10 20]) >> grid on
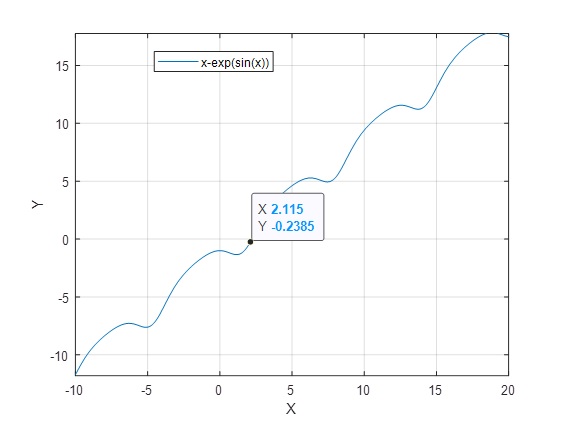
Con intersección:
>> m=@(x) exp(sin(x)); >> n=@(x) x; >> fplot(m,[0 5]) >> hold on >> fplot(n,[0 5]) >> grid on >> hold off
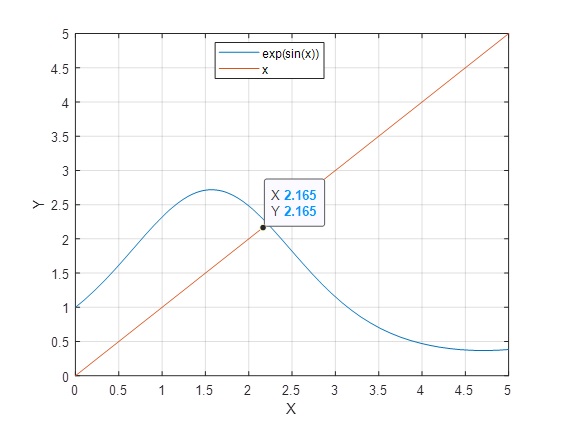
Con
>> fzero(g,[2 3])
ans = 2.2191
Ejemplo 5:
>> f=@(x) sqrt(x)-2*log(x); %D(f)=(0, ∞). >> fplot(f,[0.05 100]) >> grid on
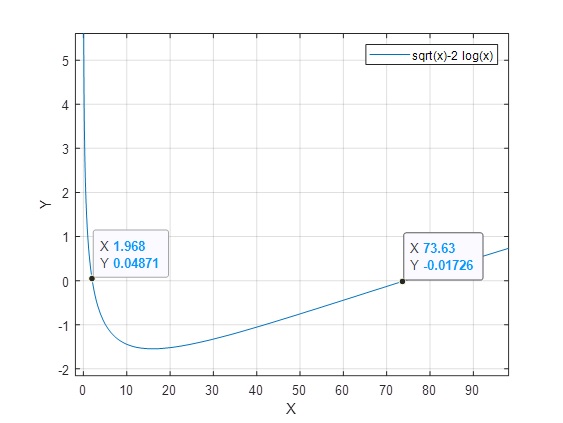
Como intersección:
>> m=@(x) sqrt(x); >> n=@(x) 2*log(x); >> fplot(m,[0.05 100]) >> hold on >> fplot(n,[0.05 100]) >> grid on >> hold off
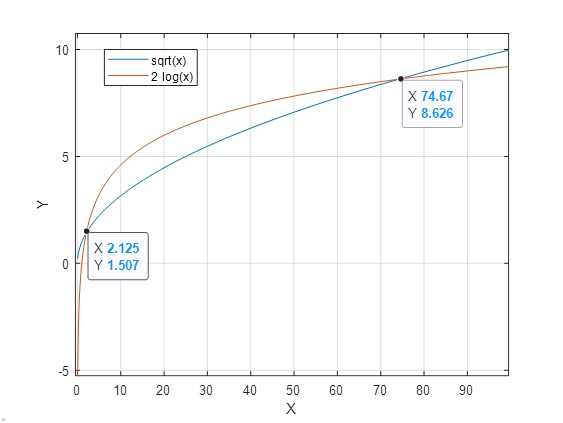
>> fzero(f,[2 3])
ans = 2.0438
>> fzero(f,[70 80])
ans = 74.1867
Ejemplo 6: x/2-3lnx
>> f=@(x) x/2-3*log(x);
>> f(0.1)
ans = 6.9578
>> f(1)
ans = 0.5000
>> f(2)
ans = -1.0794
Hay una raíz en [1 2].
>> f(15)
ans = -0.6242
>> f(20)
ans = 1.0128
Hay otra raíz en [15 20].
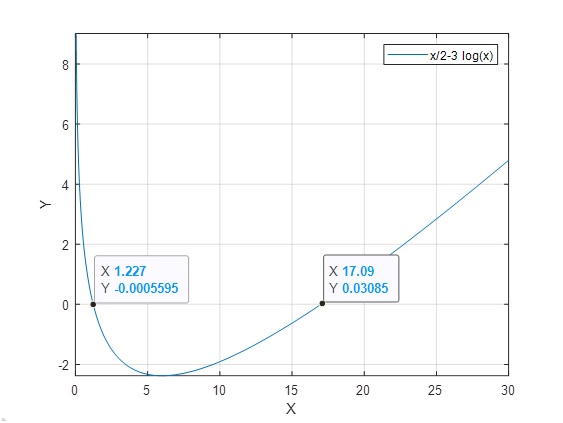
>> fzero(f,[1 2])
ans = 1.2269
>> fzero(f,[15 20])
ans = 16.9989
Ejemplo 7: lnx-2cosx=0
>> f=@(x) log(x)-2*cos(x); >> fplot(f,[0.5 50]) >> grid on
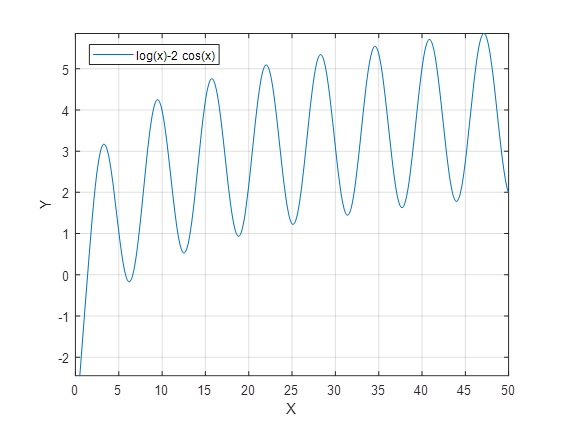
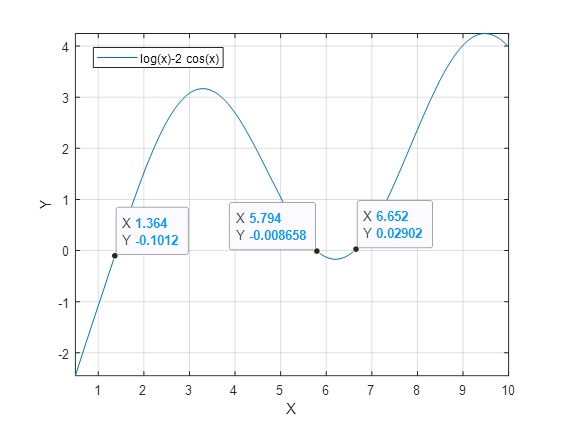
Tiene tres raíces.
>> m=@(x) log(x); >> n=@(x) 2*cos(x); >> fplot(m,[0.5 10]) >> grid on >> fplot(n,[0.5 10]) >> hold off
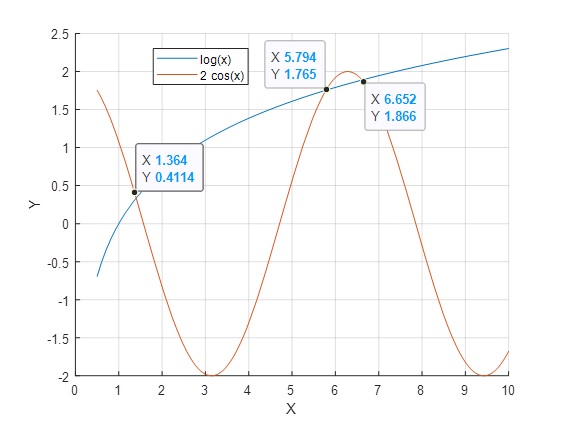
>> fzero(f,[1 2])
ans = 1.4013
>> fzero(f,[5 6])
ans = 5.7829
>> fzero(f,[6 7])
ans = 6.6169
Ejemplo 8: lnx-2senx=0
>> f=@(x) log(x)+2*sin(x); >> fplot(f,[0.1,20]) >> grid on
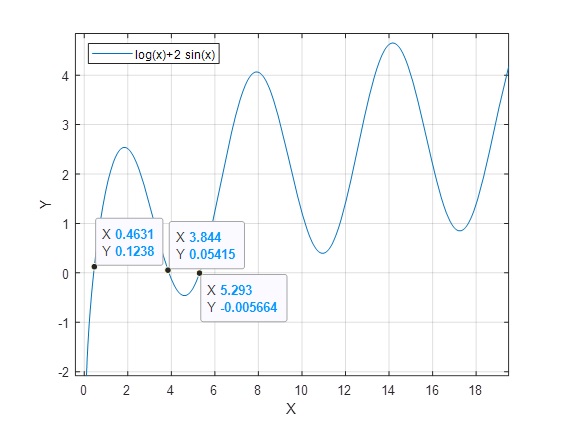
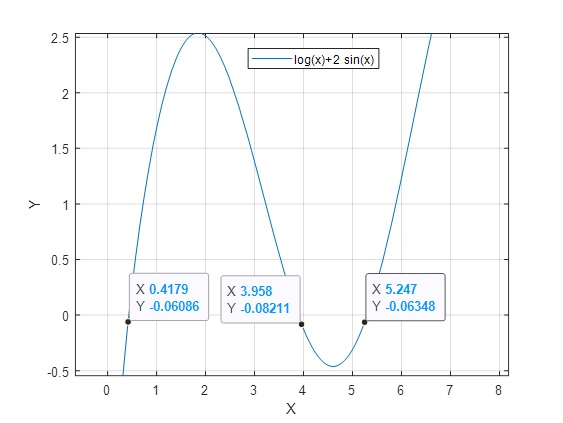
>> m=@(x)log(x); >> n=@(x)-2*sin(x); >> fplot(m,[0 8]) >> grid on >> hold on >> fplot(n,[0 8]) >> hold off
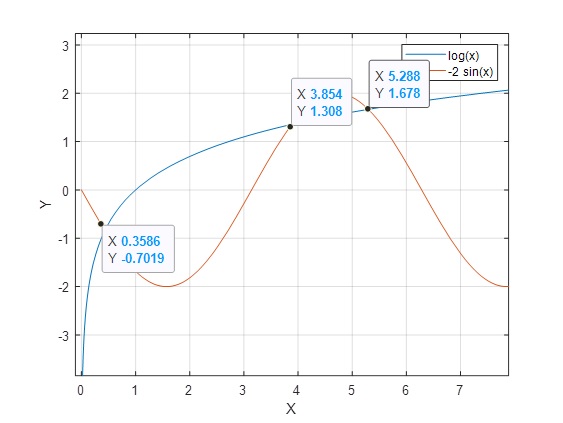
Con
>> fzero(f,[0.1,2])
ans = 0.4325
>> fzero(f,[3,4])
ans = 3.8879
>> fzero(f,[5,6])
ans= 5.2976
Ejemplo 9: 2x-e-senx=0
>> f=@(x) 2*x-exp(-sin(x));
>> f(1)
ans = 1.5689
>> f(0)
ans = -1
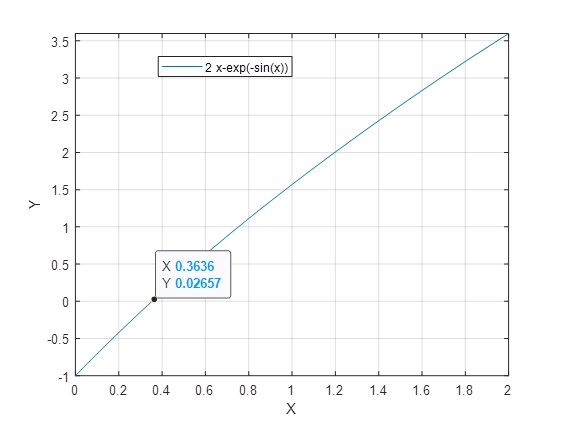
>> m=@(x)2*x; >> n=@(x) exp(-sin(x)); >> fplot(m,[-1 1]) >> grid on >> hold on >> fplot(n,[-1 1]) >> hold off
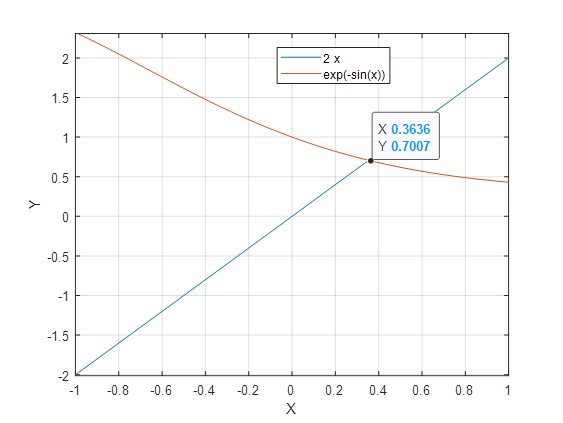
>> fzero(f,[-1 1])
ans = 0.3536
Ejemplo 10: x2+15cosx=0
>> f=@(x) x.^2+15*cos(x); %función par >> fplot(f,[-5 5]) >> grid on
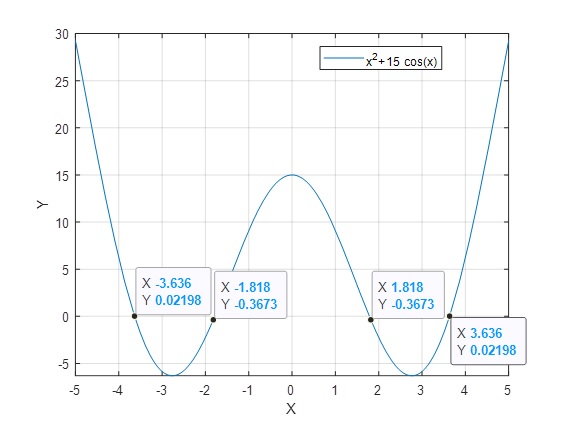
>> fzero(f,[1,2])
ans = 1.7848
>> fzero(f,[3,4])
ans = 3.6348
Ejemplo 11: ln(x/7)-senx=0
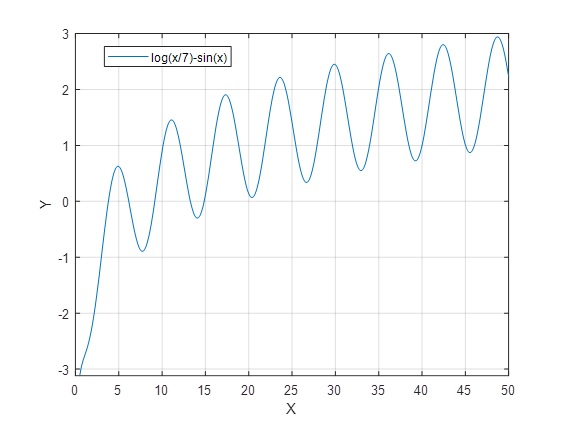
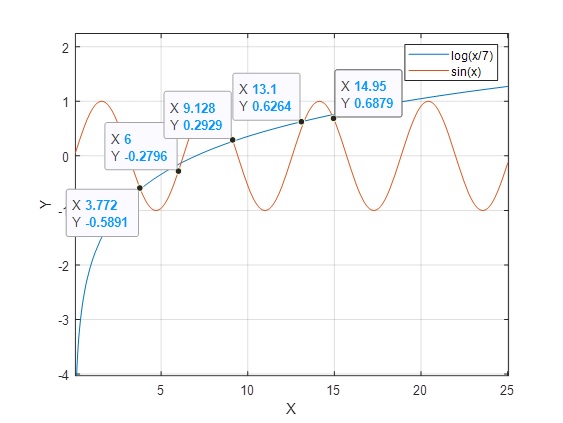
>> m=@(x) log(x/7);
>> n=@(x) sin(x);
>> fplot(m,[0.05 25])
>> hold on
>> fplot(n,[0.05 25])
>> grid on
>> hold off
>> fzero(f,[1 5])
ans = 3.7991
>> fzero(f,[5 8])
ans = 6.1540
>> fzero(f,[8 10])
ans = 9.1533
>> fzero(f,[10 14])
ans = 13.2593
>> fzero(f,[14 19])
ans = 14.8561
Método de las aproximaciones sucesivas
Supongamos la ecuación f(x)=0, siendo f(x) una función continua en el dominio donde estamos trabajando.
Sustituimos f(x)=0 por una ecuación equivalente x=g(x) (no siempre se puede hacer). En el ejemplo anterior
Suponiendo un valor aproximado de la raíz x0, lo sustituimos en g(x) y obtenemos x1=g(x0), lo volvemos a sustituir y tenemos x2=g(x1) y así, sucesivamente, xn=g(xn-1)
Si existe , p es la raíz buscada
Elaboramos el siguiente script
x0=input('valor inicial: ');
iter=input('número de iteraciones: ');
for i=1:iter
x=exp(x0)/3;
x0=x;
end
disp(x)
y lo guardamanos en el fichero
>> trascendente
valor inicial: 0
número de iteraciones: 12
0.6180
>> trascendente
valor inicial: 0
número de iteraciones: 20
0.6190
Vemos que depende del número de iteraciones que le ponemos.
Nota.-También podemos poner x=f(x0)) (genérico) si previamente hemos puesto
f=@(x) exp(x)/3;
x0=input('valor inicial: ');
iter=input('número de iteraciones: ');
for i=1:iter
x=f(x0);
x0=x;
end
disp(x)
Sin embargo, si en vez de utilizar un script genérico lo hacemos como una función genérica, hay que hacer llamada a la función ejemplo:
function x = transc(f,x0,a)
for i=1:a
x=f(x0);
x0=x;
end
end
Sabemos que tiene otra solución x= 1.5121. Por mucho que pongamos el valor inicial cercano
>> trascendente
valor inicial: 1.5
número de iteraciones: 50
0.6191
Con este método, si hemos encontrado g(x) a partir de la ecuación que nos daban, pero cuando la derivada de g(x) en valor absoluto en un entorno de la solución es mayor que la unidad no nos sirve, pues la sucesión {xn} diverge (no sirve si es >1).
Poniendo h(x)=g'(x):
>> h=@(x) exp(x)/3;
>> h(1.4)
ans = 1.3517
No lo cumple, sin embargo
>> h(0.5)
ans = 0.5496
Si tomamos otro ejemplo: x-cosx=0.
g(x)=cosx, g'(x)=-senx, cumple la condición. Tenía una solución 0.7391
>> g=@(x) cos(x);
>> x=transc(g,0,10)
x = 0.7314
>> x=transc(g,0,20)
x = 0.7389
>> x=transc(g,0,40)
x = 0.7391
Vemos las diferencias según el número de iteraciones que ponemos. Debido a esto, tendremos que poner una condición de FINALIZACION para obtener la solución con una precisión determinada. Mediante el error relativo:
Para ello sustituimos el bucle
x0=input('valor inicial: ');
Error=0.00001;
while(1)
x=exp(x0)/3;
if abs((x-x0)/x)<Error
break
end
x0=x;
end
disp(x)
Nota:
Lo guardamos en el fichero
>> trascendente1
valor inicial: 0
0.6191
También lo podemos hacer con una función (poniendo diferentes valores iniciales y errores).
function x = raiz(x0, a)
while(1)
x=exp(x0)/3;
if abs((x-x0)/x)<
break
end
x0=x;
end
end
La llamada
>> raiz(0,0.00001)
ans = 0.6191
Alternativamente, con un script
x0=input('valor inicial: ');
Error=0.00001;
while(1)
x=exp(x0)/3;
if abs((x-x0)/x)<Error
break
end
x0=x;
end
disp(x)
Lo guardamos en el fichero
>> raiz2
valor inicial: 0
0.6191
Podemos generalizar el método (no dependa de g(x)) de la siguiente manera:
function x=generalizacion(f,x0,error)
while (1)
x=f(x0);
if abs((x-x0)/x)<error
break
end
x0=x;
end
end
En la ventana de Command Window definimos
>> f=@(x) exp(x)/3;
>> generalizacion(f,0,0.000001)
ans = 0.6191
>> g=@(x) cos(x);
>> generalizacion(g,0,0.000001)
ans = 0.7391
Ejercicios
x/4-lnx=0
2x-e-senx=0
x-5ln(3x)=0
Soluciones
Ejercicio 1: x/4-lnx=0
>> f=@(x)x/4-log(x); >> fplot(f,[0.01 10]) >> grid on
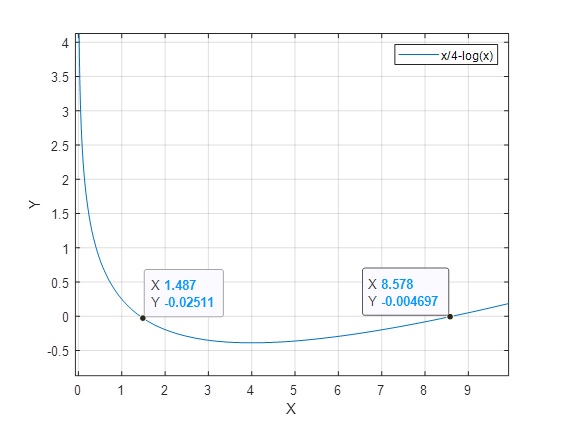
>> g=@(x) 4*log(x);
>> x=transc(g,1.1,10)
x = 8.6394 + 0.0282i
>> format long
>> x=transc(g,7,100)
x = 8.613169456441398
>> x=generalizacion(g,3,0.0000001)
x = 8.613169065093460
>> x=generalizacion(g,20,0.0000001)
x = 8.613169999242976
>> x=generalizacion(g,10,0.0000001)
x = 8.613170022952085
No nos saca la otra raíz.
g'(x)=4/x, en puntos próximos a la otra raíz, por ejemplo: (4/1.4=2.85>1)
>> fzero(f,[1 2])
ans = 1.429611824725556
>> fzero(f,[8 9])
ans = 8.613169456441399
Ejercicio 2: 2x-e-senx=0
Ya se ha resuelto gráficamente
>> f=@(x) 2*x-exp(-sin(x));
>> fzero(f,[-1 1])
ans = 0.353643666364288
>> g=@(x) exp(-sin(x))/2;
>> x=transc(g,0,10)
x = 0.353637059442602
>> x=transc(g,0,100)
x = 0.353643666364288
>> x=generalizacion(g,0,0.000000001)
x = 0.353643666399692
Lo mismo, simplificado:
> x=generalizacion(g,0,1.e-9)
x = 0.353643666399692
>> x=generalizacion(g,0,1.e-29)
x = 0.353643666364288
Ejercicio 3: x-5ln(3x)=0
>> f=@(x) x-5*log(3*x); >> fplot(f,[0.1,30]) >> grid on
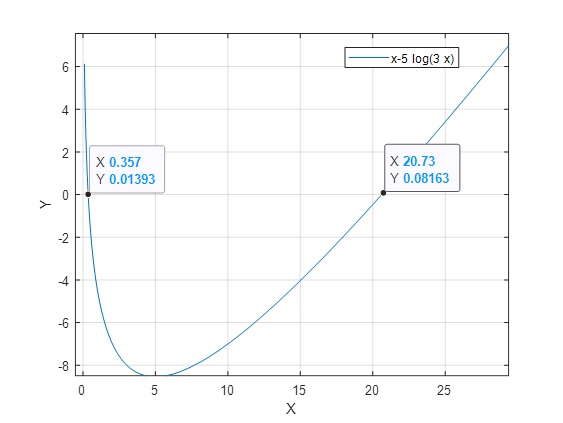
>> g=@(x)5*log(3*x);
>> x=transc(g,1,30)
x = 20.625767053302223
>> x=transc(g,1,50)
x = 20.625767053302223
No cambia
>> x=generalizacion(g,0.4,1e-2)
x = 20.593807088453154
>> x=generalizacion(g,0.4,1e-20)
x = 20.625767053302223
No obtenemos la otra solución, pues la derivada en los puntos próximos es mayor que uno.
>> fzero(f,[0.1 1])
ans = 0.358080989401766
>> fzero(f,[19 23])
ans = 20.625767053302219
Método de Newton-Raphson
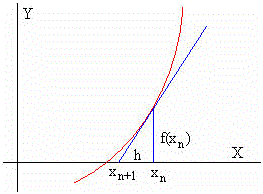
Si desarrollamos la función f(x+h) en serie de Taylor en el punto x:
f(x+h) =f(x)+f'(x)·h+...
Si h es pequeño podemos despreciar los términos en, h2, h3... Si x+h es raíz de la ecuación
Creamos un desarrollo iterativo que nos permita calcular la raíz de la siguiente forma:
Definimos el procedimiento de Newton-Raphson de forma análoga al anterior de las aproximaciones sucesivas.
function x=newton_raphson(f,f_prima,x0,error)
while(1)
x=x0-f(x0)/f_prima(x0);
if abs((x-x0)/x)<error
break
end
x0=x;
end
end
Repitiendo el mismo ejemplo:
>> f=@(x) x-exp(x)/3;
>> f_prima=@(x) 1-exp(x)/3;
>> format long
>> newton_raphson(f,f_prima,0.5,0.00001)
ans = 0.619061286735945
Para la otra raíz:
>> newton_raphson(f,f_prima,1.4,0.000001)
ans = 1.512134551659757
Ejemplos
Ejemplo, que fallaba por el método de aproximaciones sucesivas
>> f=@(x) 5*x^2-exp(x);
>> f_prima=@(x) 10*x-exp(x);
>> x=newton_raphson(f,f_prima,0,0.00000001)
x = -0.371417752459174
>> x=newton_raphson(f,f_prima,1,0.00000001)
x = 0.605267121314618
>> x=newton_raphson(f,f_prima,4,0.00000001)
x = 4.707937918128859
Ejemplo, que fallaba por el método de aproximaciones sucesivas
>> f=@(x)x/4-log(x);
>> f_prima=@(x) 1/4-1/x;
>> x=newton_raphson(f,f_prima,1,0.00000001)
x = 1.429611824725556
>> x=newton_raphson(f,f_prima,8,0.00000001)
x = 8.613169456441398
Haciendo con un bucle
function x = Rahfor(f,f_prima,x0,iter)
for i=1:iter
x=x0-f(x0)/f_prima(x0);
x0=x;
end
end
>> x=Rahfor(f,f_prima,1,100)
x = 1.429611824725556
>> x=Rahfor(f,f_prima,8,100)
x = 8.613169456441398
Método del punto medio o bisección
Este método se basa en el teorema de Bolzano que nos dice:
Si una función f(x) es continua en un intervalo [a, b] y en los extremos del intervalo toma valores de signo opuesto, entonces existe, al menos, un valor c interior al intervalo donde f(c)=0.
Tenemos la ecuación f(x)=0, donde la función f(x) cumple las condiciones de Bolzano.
Repitiendo el proceso obtenemos una sucesión de intervalos:
Nos podemos plantear el error de cálculo de dicha raíz. Si queremos que sea menor que ε
Condiciones de terminación del proceso
Vamos a considerar que la función f(x)) es nula cuando en valor absoluto es menor que una cantidad muy pequeña:
El proceso se debe acabar en un momento determinado. Podemos elegir cuando:
El proceso finalizará después de un número fijado de iteraciones, notificando que no ha encontrado la raíz con las condiciones establecidas.
function m = mediofor(f,a,b,error,iter)
for i=1:iter
m=(a+b)/2;
if abs((b-a)/m)<error
break
elseif f(a)*f(m)<0
b=m;
else
a=m;
end
end
end
Aplicado a nuestro ejemplo:
>> f=@(x) 3*x-exp(x);
>> m= mediofor(f,-1,1,1e-10,20)
m = 0.619062423706055
>> m= mediofor(f,-1,1,1e-10,200)
m = 0.619061286764918
>> fzero(f,[-1,1])
ans = 0.619061286735945
Para el otro punto
>> m=mediofor(f,1,2,1e-10,200)
m = 1.512134551710915
>> m=mediofor(f,1,2,1e-10,1000)
m = 1.512134551710915
>> fzero(f,[1,2])
ans = 1.512134551657843
Con un bucle
function m = mediowh( f,a,b,error )
while(1)
m=(a+b)/2;
if abs((b-a)/m)<error
break
elseif f(a)*f(m)<0
b=m;
else
a=m;
end
end
end
>> m=mediowh(f,-1,1,1e-20)
m = 0.619061286735946 0.619061286735945(fzero)
>> m=mediowh(f,1,2,1e-20)
m = 1.512134551657844 1.512134551657843(fzero)
La diferencia es que con el
Para el otro ejercicio:
>> f=@(x) x/2-3*log(x);
>> m=punto_medio(f,1,2,40)
m = 1.226867675781250
>> m=punto_medio(f,10,20,40)
m = 16.998901367187500
Ejemplos
-
Otro ejemplo hecho:
>> f=@(x)x/4-log(x);
>> m=punto_medio(f,1, 2,50)
m = 1.429626464843750
>> m=punto_medio(f,1, 2,500)
m = 1.429626464843750
>> m=punto_medio(f,6, 9,500)
m = 8.612915039062500
Ejemplo: x2-cosx=0, que es una función par
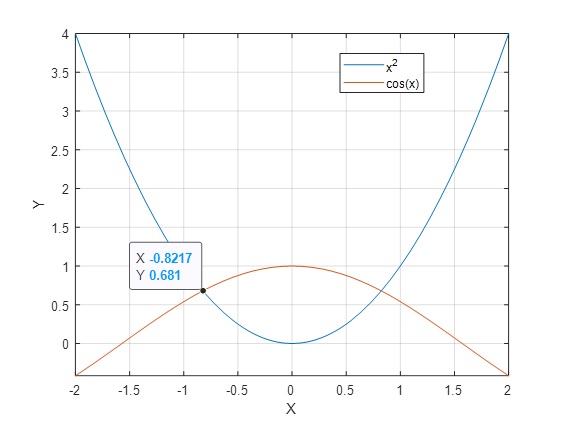
>> u=@(x) x^2-cos(x);
>> fzero(u,[0 1])
ans = 0.824132312302522
>> fzero(u,[-1 0])
ans = -0.824132312302522
>> v=@(x) 2*x+sin(x);
>> x=newton_raphson(u,v,1,1.e-9)
x = 0.824132312302522
>> x=Rahfor(u,v,1,10)
x = 0.824132312302522
>> x=punto_medio(u,-1,0,20)
x = -0.824127197265625
>> x=punto_medio(u,-1,0,200)
x = -0.824127197265625
Ejemplo: x2+15cosx=0
>> s=@(x) x.^2; >> t=@(x) -15*cos(x); >> fplot(s,[-5 5]) >> hold on >> fplot(t,[-5 5]) >> grid on >> hold off
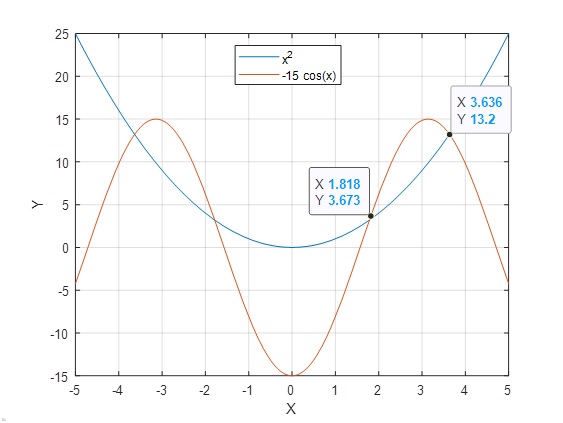
Al ser par tiene los simétricos.
Newton-Raphson
while
>> u=@(x) x^2+15*cos(x);
>> v=@(x) 2*x-15*sin(x);
>> x=newton_raphson(u,v,1,1.e-7)
x = 1.784791163424146
>> x=newton_raphson(u,v,3,1.e-7)
x = 3.634835618651561
>> x=Rahfor(u,v,1,100)
x = 1.784791163424146
>> x=Rahfor(u,v,3,10)
x = 3.634835618651561
>> x=Rahfor(u,v,3,2)
x = 3.778867298500717
Punto medio
while
>> x= mediowh(u,1,2,1.e-10)
x = 1.784791163459886
>> x= mediowh(u,3,4,1.e-10)
x = 3.634835618664511
>> x=punto_medio(u,1,2,500)
x = 1.784851074218750
>> x=punto_medio(u,1,2,5)
x = 1.781250000000000
>> x=punto_medio(u,3,4,50)
x = 3.634887695312500
fzero
>> fzero(u,[1 2])
ans = 1.784791163424146
>> fzero(u,[3 4])
ans = 3.634835618651561

