Integración numérica |
Análisis de Fourier de una función periódica
La definición de la función f(t).
La aproximación de una función periódica mediante una suma de armónicos es un problema importante en las Matemáticas, la Física y las Ingenierías, baste citar todos los fenómenos vibratorios, ondulatorios que son fundamento de la acústica, de las telecomunicaciones, etc.
En esta página, procederemos a obtener los coeficientes del desarrollo en serie de Fourier de una función periódica. Primero, se explicará brevemente cómo se representan las funciones periódicas mediante series de Fourier uniformemente convergentes, y posteriormente, se explicarán los pasos necesarios para crear una clase denominada Fourier que nos calculará los primeros coeficientes del desarrollo en serie.
Toda función f(t) periódica de periodo P, se puede representar en forma de una suma infinita de funciones armónicas, es decir,
![]()
donde el periodo P=2p/w, y a0, a1, ...ai ... y b1, b2, .... bi .... son los denominados coeficientes de Fourier.
Toda función periódica de periodo P, se puede transformar en una función periódica de periodo 2p, mediante un simple cambio de escala en el eje t. Escribiendo x=wt, tendremos el periodo P de t convertido en el periodo 2p de x, y la función f(t) convertida en
![]()
definida en el intervalo que va de -p a +p. La serie se expresa en la forma más simple
![]()
donde
![]()
![]()
Si la función g(x) tiene simetría, algunos de los coeficientes resultan nulos.
- Si g(x) es una función par, g(x)=g(-x), los términos bi son nulos
- Si g(x) es impar g(x)=-g(-x), los coeficientes ai son nulos
- Si g(x) es alternada, g(x+p)=-g(-x), la serie solamente consta de términos armónicos impares.
Para codificar el procedimiento de análisis de Fourier de una función periódica, seguiremos el esquema trazado en otros ejmplos: la clase base abstracta denominada Fourier definirá el procedimiento numérico, y las clases derivadas denominadas Funcion1, Funcion2, etc. definirán las funciones periódicas cuyos coeficientes de Fourier deseamos calcular.
Si la función periódica es discontinua, como en el caso de un pulso rectangular, un pulso escalón, un pulso en forma de diente de sierra, etc., es necesario declarar y definir una función f0, f1, f2, ... en cada uno de los intervalos contiguos, (t0, t1), (t1, t2), ... tal como se ve en la figura
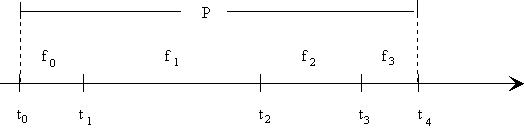
Los puntos de discontinuidad ti, se guardan en el array tiempo. En el constructor de la clase base Fourier se reserva espacio para dicho array. Sea por ejemplo el pulso diente de sierra de la figura
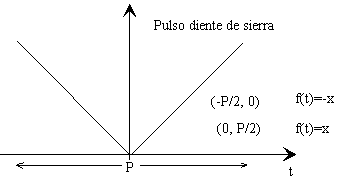
double[] tiempo=new double [3];
tiempo[0]=-periodo/2;
tiempo[1]=0.0;
tiempo[2]=periodo/2;
Como vemos el array tiempo guarda las abscisas que señalan las discontinuidades de la función incluidos los extremos del periodo.
Este array se pasa al constructor de la clase derivada de Fourier, la cual define la función periódica en cada uno de los intervalos.
public class Funcion3 extends Fourier {
public Funcion3(double[] discont) {
super(discont);
}
public double funcion(double t){
if(iDiscont==0) return -t;
return t;
}
}
Donde iDiscont es un miembro dato de la clase base Fourier que señala el intervalo actual, en el que se está efectuando la integración.
El constructor de la clase derivada pasa el array de discontinuidades a la clase base, el cual las guarda cambiadas de escala en el miembro array x, y el número de discontinuidades en el miembro nDiscont.
public abstract class Fourier {
double[] x; //discontinuidades
int nDiscont; //número de discontinuidades
double P; //periodo
public Fourier(double[] tiempo) {
nDiscont=tiempo.length;
P=tiempo[nDiscont-1]-tiempo[0];
//...
}
Ahora, transformamos la función periódica de periodo P, en una función periódica definida en el intervalo de -p a p, es decir, de periodo 2p. Los nuevos puntos de discontinuidad xi, se guardan el array x, de la misma dimensión que el array tiempo. Las fórmulas de transformación son
![]()
![]()
y su codificación.
x=new double[nDiscont];
x[0]=-Math.PI;
x[nDiscont-1]=Math.PI;
for(int i=1; i<nDiscont-1; i++){
x[i]=(tiempo[i]-tiempo[0])*2*Math.PI/(tiempo[nDiscont-1]-tiempo[0])-Math.PI;
}
Para hallar un coeficiente ai, se ha de integrar cada una de las funciones fk que definen la función periódica f(t), efectuar el cambio de escala cambiando la variable t por la variable x, multiplicarla por la función cos(ix), y sumando los resultados para todos los intervalos (xk, xk+1)
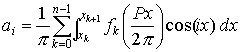
Una expresión similar se emplea para calcular los coeficientes bi.
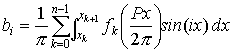
Si tenemos en cuenta la propiedad de que sin(q+p/2)=cos(q), ambas expresiones pueden convertirse en una única expresión
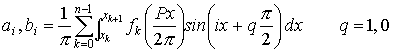
Los coeficientes ai, se obtienen cuando la variable de control q es uno, y los coeficientes bi cuando la variable q es cero. La función integrando se define del siguiente modo.
double f(double x){
double y=funcion((x*P)/(2*Math.PI))*Math.sin(iArmonico*x+q*Math.PI/2);
return y;
}
La integral se efectúa aplicando el método de Simpson,
Para hallar la contribución de cada una de las funciones, se pasan a la función integral el comienzo del intervalo, xk, en el parámetro a, el final del intervalo xk+1, en el parámetro b, y el número de divisiones de dicho intervalo en el parámetro n.
El número de divisiones se calcula mediante una simple regla de tres: si a todo el periodo 2p le corresponden, por ejemplo, 100 divisiones, al intervalo de longitud xi+1-xi le corresponderán ni divisiones. Los números enteros obtenidos se guardan en el array nDivisiones de dimensión nDiscont-1.
nDivisiones=new int[nDiscont-1];
//se asignana 100 divisiones para el intervalo 0 - 2PI
for(int i=0; i<nDiscont-1; i++){
nDivisiones[i]=(int)((x[i+1]-x[i])*50/Math.PI);
}
El cálculo de los coeficientes tiene lugar en la función miembro denominada calcular. Los coeficientes se guardan en dos arrays a y b. Se crean estos dos arrays y se inicializan a cero en el constructor.
static final int MAX_ARMONICOS=11;
double[] a=new double[MAX_ARMONICOS];
double[] b=new double[MAX_ARMONICOS];
for(int i=0; i<MAX_ARMONICOS; i++){
a[i]=b[i]=0.0;
}
Para calcular el coeficiente aj, se da a la variable entera de control q el valor de uno, y se suman las contribuciones de todas las nDiscont-1 discontinuidades al armónico de orden j. El resultado de divide entre p. Se repite el cálculo para todos los coeficientes a menores que MAX_ARMONICOS.
q=1; //coseno
for(iArmonico=0; iArmonico<MAX_ARMONICOS; iArmonico++){
for(iDiscont=0; iDiscont<nDiscont-1; iDiscont++){
a[iArmonico]+=integral(x[iDiscont], x[iDiscont+1],
nDivisiones[iDiscont])/Math.PI;
}
}
Para hallar los coeficientes b, se efectúa el mismo cálculo solamente que la variable de control q, pasa a valer cero.
q=0; //seno
for(iArmonico=0; iArmonico<MAX_ARMONICOS; iArmonico++){
for(iDiscont=0; iDiscont<nDiscont-1; iDiscont++){
b[iArmonico]+=integral(x[iDiscont], x[iDiscont+1],
nDivisiones[iDiscont])/Math.PI;
}
}
La función mostrarCoeficientes primero llama a la función calcular y luego, muestra los coeficientes con tres cifras decimales. primero a0 y luego, los coeficientes ai al lado de los coeficientes bi del mismo orden.
void mostrarCoeficientes(){
calcular();
System.out.println("a[0] "+a[0]);
for(int i=1; i<MAX_ARMONICOS; i++){
System.out.println("a["+i+"]="+Math.floor(a[i]*1000)/1000+
"\t"+"b["+i+"]="+Math.floor(b[i]*1000)/1000);
}
}
El código completo de la clase base abstracta Fourier es el siguiente
public abstract class Fourier {
//coeficientes de Fourier
public static final int MAX_ARMONICOS=11;
public double[] a=new double[MAX_ARMONICOS];
public double[] b=new double[MAX_ARMONICOS];
//discontinuidades
protected int nDiscont;
protected int iDiscont; //discontinuidad actual
protected double P; //periodo
//variables de control
private int iArmonico=0; //armónico
private int q=1; //seno o coseno
//número de divisones en cada intervalo
private int[] nDivisiones;
private double[] x;
public Fourier(double[] tiempo, int nDiscont) {
this.nDiscont=nDiscont;
//periodo
P=tiempo[nDiscont-1]-tiempo[0];
//transformación de variable, de perido P a perido 2PI
x=new double[nDiscont];
x[0]=-Math.PI;
x[nDiscont-1]=Math.PI;
for(int i=1; i<nDiscont-1; i++){
x[i]=(tiempo[i]-tiempo[0])*2*Math.PI/(tiempo[nDiscont-1]-tiempo[0])-Math.PI;
}
for(int i=0; i<MAX_ARMONICOS; i++){
a[i]=b[i]=0.0;
}
nDivisiones=new int[nDiscont-1];
}
//método de Simpson
protected double integral(double a, double b, int n){
double h;
double s;
//el número de divisiones debe ser par
if(n%2==1) n++;
h=(b-a)/n;
s=f(a)-f(b);
for(int i=1; i<n; i+=2){
s+=4*f(a+i*h)+2*f(a+(i+1)*h);
}
return (s*h/3);
}
abstract public double funcion(double t);
private double f(double x){
double y=funcion((x*P)/(2*Math.PI))*Math.sin(iArmonico*x+q*Math.PI/2);
return y;
}
public void calcular(){
//se asignana 100 divisiones para el intervalo 0 - 2PI
for(int i=0; i<nDiscont-1; i++){
nDivisiones[i]=(int)((x[i+1]-x[i])*50/Math.PI);
}
//calcula los coeficientes a
q=1; //coseno
for(iArmonico=0; iArmonico<MAX_ARMONICOS; iArmonico++){
for(iDiscont=0; iDiscont<nDiscont-1; iDiscont++){
a[iArmonico]+=integral(x[iDiscont], x[iDiscont+1], nDivisiones[iDiscont])/Math.PI;
}
}
//calcula los coeficientes b
q=0; //seno
for(iArmonico=0; iArmonico<MAX_ARMONICOS; iArmonico++){
for(iDiscont=0; iDiscont<nDiscont-1; iDiscont++){
b[iArmonico]+=integral(x[iDiscont], x[iDiscont+1], nDivisiones[iDiscont])/Math.PI;
}
}
}
public void mostrarCoeficientes(){
calcular();
System.out.println("a[0] "+a[0]);
for(int i=1; i<MAX_ARMONICOS; i++){
System.out.println("a["+i+"]="+Math.floor(a[i]*1000)/1000+"\t"+"b["+i+"]="+Math.floor(b[i]*1000)/1000);
}
}
}
|