|
Las matrices cuadradas |
Valores propios y vectores propios
El cálculo de los valores propios y de los vectores propios de una matriz simétrica tiene gran importancia en las matemáticas y en la ingeniería, entre los que cabe destacar, el problema de la diagonalización de una matriz, el cálculo de los momentos de inercia y de los ejes principales de inercia de un sólido rígido, o de las frecuencias propias de oscilación de un sistema oscilante.
Se denominan valores propios o raíces características de una matriz cuadrada A, a los valores de l tales que.
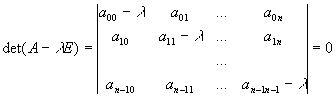
Desarrollando el determinante tenemos un polinomio de grado n. Trataremos de encontrar los coeficientes del polinomio, y luego aplicaremos un método de hallar las raíces del polinomio. Este procedimiento es apropiado cuando se presentan valores propios que no son reales sino complejos.
Una vez hallados los valores propios, para hallar el vector propio X correspondiente al valor propio l es necesario resolver el sistema homogéneo
donde el vector X es 
Siempre podemos
tomar x0 como 1, y hallar las otras n-1 incógnitas. De las n
ecuaciones podemos tomar n-1, y resolver el sistema lineal.
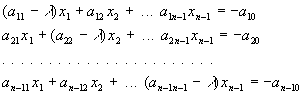
Dada una matriz cuadrada A de dimensión n. El polinomio característico de la matriz es
Los coeficientes se hallan mediante las siguientes relaciones
(1)
Los valores s1, s2, ... sn son las trazas de las potencias de la matriz cuadrada A.
La traza de una matriz es la suma de los elementos de su diagonal principal.
La codificación en términos de la clase Matriz no reviste dificultad, y tiene dos partes, en la primera se calcula las potencias de la matriz A, y la traza de cada una de ellas, en segundo lugar se calculan los coeficientes pi del polinomio característico. Para hallar las potencias de la matriz A se emplea un código similar al que empleamos para hallar las potencias de un número. En aquella ocasión la potencia de orden cero de un número es la unidad, en este caso es la matriz unidad de la misma dimensión que A.
Matriz pot=new Matriz(n);
for(int i=0; i<n; i++){
pot.x[i][i]=1.0;
}
Luego, se calcula las trazas de las distintas matrices pot cuando se van elevando ésta (this) a las sucesivas potencias llamando a la función miembro traza de la clase Matriz, y la guarda en el array s.
for(int i=1; i<=n; i++){
pot=Matriz.producto(pot, this);
s[i]=pot.traza();
El polinomio característico tiene por primer coeficiente la unidad, el resto de los coeficientes se calculan codificando las relaciones (1) en un doble bucle.
p[0]=1.0;
p[1]=-s[1];
for(int i=2; i<=n; i++){
p[i]=-s[i]/i;
for(int j=1; j<i; j++){
p[i]-=s[i-j]*p[j]/i;
}
}
Una vez calculados todos los coeficientes del polinomio característicos, la función devuelve el array p. El código completo de la función polCracteristico es el siguiente.
public double[] polCaracteristico(){
Matriz pot=new Matriz(n);
//matriz unidad
for(int i=0; i<n; i++){
pot.x[i][i]=1.0;
}
double[] p=new double[n+1];
double[] s=new double[n+1];
//potencias de la matriz y traza
for(int i=1; i<=n; i++){
pot=Matriz.producto(pot, this);
s[i]=pot.traza();
}
//coeficientes del polinomio característico
p[0]=1.0;
p[1]=-s[1];
for(int i=2; i<=n; i++){
p[i]=-s[i]/i;
for(int j=1; j<i; j++){
p[i]-=s[i-j]*p[j]/i;
}
}
return p;
}
|
Hallar el polinomio característico de la matriz
El desarrollo del determinante secular mediante el método de Leverrier conduce a la ecuación
A continuación aplicaremos un método de cálculo de las raíces de un polinomio.
double[][] p1={{1,2,3,4},{2,1,2,3},{3,2,1,2},{4,3,2,1}};
Matriz p=new Matriz(p1);
double pol[]=p.polCaracteristico();
System.out.println("Polinomio característico");
for(int i=0; i<pol.length; i++){
System.out.print((double)Math.round(pol[i]*1000)/1000+" , ");
}
System.out.println("");