El método mitad (raíz simple)

El método mitad es uno de los métodos más sencillos de comprender y es muy conveniente para dar rápidamente con la raíz de la ecuación dada, sin embargo, el número de cálculos aumenta sustancialmente a medida que se desea mayor exactitud.

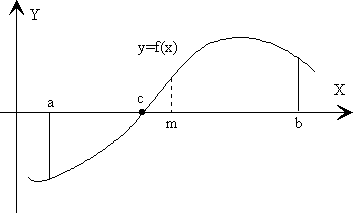
El procedimiento mitad se basa en el teorema de Bolzano que dice que si tenemos una función y=f(x), de variable real y continua en el intervalo (a, b), y el signo de la función en el extremo a es distinto al signo de la función en el extremo b del intervalo, existe al menos un valor c dentro de dicho intervalo (a, b) tal que f(c)=0, c es por tanto, la raíz buscada, véase la figura.

Supongamos una ecuación

Para hallar la raíz de la función en el intervalo (a, b), se divide el intervalo en la mitad.

(3)

Pueden ocurrir uno de estos tres casos:

Si f(m)=0 entonces m es la raíz buscada
Si f(a) y f(m) tienen signos contrarios, como en la figura, la raíz buscada está en el intervalo (a, m).
Si no se cumple la condición anterior, f(b) y f(m) tendrían signos contrarios y la raíz estaría en el intervalo (m, b).

El nuevo intervalo reducido se divide por la mitad y se procede de igual forma. Finalmente, en una cierta etapa del proceso tendremos bien la raíz exacta de la función f(x), o una secuencia de intervalos cada vez más reducidos (a₁, b₁), (a₂, b₂), .... (a_i, b_i)... tal que

Como los puntos extremos de la izquierda a₁, a₂, ... a_n, ...forman una sucesión creciente y acotada, y los de la derecha b₁, b₂, ... b_n, ... una sucesión acotada decreciente, existe un límite común que es la raíz x buscada.

Las condiciones de terminación del proceso

El ordenador trabaja con números de precisión limitada, por lo que tendremos que poner un criterio que establezca cuando la función f(x) se considera nula. Diremos que f(x) es nula cuando el valor absoluto de f(x) sea menor que una cantidad pequeña pero no nula e₁.

No podemos programar un proceso indefinido, es preciso, que la rutina repetitiva acabe en un momento dado. El criterio empleado es el siguiente

Siendo e₂ cierta cantidad prefijada. La raíz se encuentra en el intervalo (a_n, b_n) y m es el punto medio de dicho intervalo.

El tercer criterio de terminación establece, que el proceso de búsqueda de la raíz se interrumpirá después de un número prefijado de iteraciones, notificándose al usuario que no se ha encontrado la raíz de la función con las condiciones fijadas en los puntos 1 y 2.

Para poder codificar este procedimiento hemos de seguir los pasos siguientes

Partimos de un intervalo (a, b) en el que la función f(x) cambia de signo
Se calcula m, abscisa mitad del intervalo mediante m=(a+b)/2
Se verifican las condiciones de terminación
Si f(a) y f(m) tienen signos contrarios, como se ve en la figura, la raíz está en el intervalo (a, m), entonces b toma el valor de m.
Si la condición anterior no es cierta, la raíz se encuentra en el intervalo (m, b), por lo que a tomará el valor de m.
Se repite el proceso hasta que se cumple una u otra condición de terminación

        do{
            m=(a+b)/2;
            ym=f(m);
            if(Math.abs(ym)<CERO)           break;
            if(Math.abs((a-b)/m)<ERROR)     break;

            if((f(a)*ym)<0)     b=m;
            else                a=m;
            iter++;
        }while(iter<MAXITER);

Raíz simple

Como en caso del procedimiento de aproximacione sucesivas, crearemos una clase base abstracta denominada Ecuacion con una función miembro denominada puntoMedio que describa el procedimiento numérico.

public abstract class Ecuacion {
    protected static final double CERO=1e-10;
    protected static final double ERROR=0.001;
    protected final int MAXITER=200;

    public double puntoMedio(double a, double b) throws RaizExcepcion{
        double m, ym;
        int iter=0;
        do{
            m=(a+b)/2;
            ym=f(m);
            if(Math.abs(ym)<CERO)           break;
            if(Math.abs((a-b)/m)<ERROR)     break;

            if((f(a)*ym)<0)     b=m;
            else                a=m;
            iter++;
        }while(iter<MAXITER);
        if(iter==MAXITER){
            throw new RaizExcepcion("No se ha encontrado la raíz");
        }
        return m;
    }

    abstract public double f(double x);
}

class RaizExcepcion extends Exception {
  public RaizExcepcion(String s) {
         super(s);
  }
}

Cuando se cumple el tercer criterio de terminación, es decir, se supera el número de iteraciones MAXITER prefijada de antemano, se lanza (throw) una excepción que indica que la raíz buscada no se ha encontrado. Para lanzar la excepción, se ha de crear un objeto de la clase derivada RaizExcepcion de la clase base Exception.

Como la clase Ecuacion es abstracta, la clase derivada de ésta Funcion1 define la función f(x) particular cuyas raíz deseamos conocer en un determinado intervalo. Sea por ejemplo, la función estudiada en la sección anterior

Como hemos visto esta función tiene una raíz en el intervalo (0, p/2). La función cambia de signo en dicho intervalo, f(0)=-1, y f(p/2)=p/2.

public class Funcion1 extends Ecuacion{
    public double f(double x){
        return(x-Math.cos(x));
    }
}

Para hallar la raíz de esta ecuación creamos un objeto de la clase derivada Funcion1, y llamamos desde éste a la función que describe el procedimiento numérico puntoMedio. Ya que la función puntoMedio puede lanzar una excepción, la llamada a dicha función se debe de efectuar en un bloque try ... catch. De este modo, se notifica al usuario que el procedimiento numérico ha sido incapaz de hallar la raíz de dicha ecuación, mediante el mensaje "No se ha encontrado la raíz" que se extrae del objeto ex de la clase RaizExcepcion mediante la función getMessage.

	Ecuacion e=new Funcion1();
        try{
            System.out.println("solución1 "+e.puntoMedio(0.5, 0.9));
        }catch(RaizExcepcion ex){
            System.out.println(ex.getMessage());
        }

Código fuente

Ecuacion.java, Funcion1.java, EcuacionApp2.java

El método mitad (raíz simple)

Raíces de una ecuación

Descripción

Las condiciones de terminación del proceso

Raíz simple

Código fuente