|
El
oscilador armónico
amortiguado por una fuerza proporcional a la velocidad, tiene las
siguientes características esenciales:
-
La amplitud decrece exponencialmente con el tiempo
-
El oscilador tarda un tiempo teóricamente infinito en
pararse
Sin embargo, el oscilador armónico amortiguado por una
fuerza de módulo constante, tiene las siguientes características:
-
La amplitud decrece una cantidad constante en cada
semioscilación
-
Se para al cabo de un tiempo finito
El oscilador armónico bajo la acción de una fuerza de
rozamiento constante, nos permite examinar una vez más, el comportamiento de
la
fuerza de rozamiento. La fuerza de rozamiento tiene un módulo constante, pero
su sentido es contrario a la velocidad del móvil.
Consideremos un bloque de masa m unido a un
muelle elástico de constante k, que desliza sobre una superficie
rugosa. Los coeficientes de rozamiento estático y cinético son
respectivamente, μs y μk, con
μ=μs = μk.
El origen O se toma como la posición de equilibrio del
muelle sin deformar. El bloque se suelta desde la posición x0
a la derecha del origen con velocidad inicial cero.
Vamos a estudiar el comportamiento del sistema desde el
punto de vista energético y a continuación, resolveremos las ecuaciones del
movimiento.
El
trabajo de la fuerza de rozamiento modifica la energía total (cinética
más potencial del bloque).
Vamos a calcular las posiciones del bloque para las
cuales, su velocidad es cero. A estas posiciones se denominan de retorno, ya
que en ellas el bloque cambia el sentido de su movimiento, hasta que
finalmente se para. Como la velocidad en las posiciones inicial y final son
nulas, la ecuación del balance energético se escribe
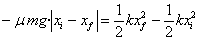
Siendo xi la posición inicial y xf
la final.
Definiremos el parámetro
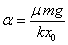
-
Posición de partida x0
El bloque se mueve hacia la izquierda si la fuerza
que ejerce el muelle kx0 es superior a la de rozamiento
μmg. En caso contrario, el bloque permanece en reposo. Supongamos
que se cumple μmg≤ kx0 o que α≤1

-
Posición x1
La ecuación del balance energético se escribe
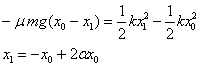
-
Si 1/2≤α≤1, el bloque no cruzará el origen y
x1≥0 será la posición final
-
Si α<1/2, el bloque cruzará el origen y x1<0
será una posición de retorno
Supongamos que ocurre la segunda situación x1<0
tal como se muestra en la figura

-
Posición x2
El móvil parte de x1 con velocidad
inicial nula siempre que se cumpla que k|x1|≥ μmg,
k(x0-2αx0)≥
μmg o bien, que α≤1/3 en caso contrario, la posición x1
será la final del bloque. Supongamos que se cumple la primera condición.
La ecuación del balance energético se escribe
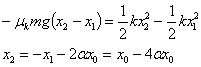
-
Si 1/4≤α≤1/3, el bloque no cruzará el origen
y x2≤0 será la posición final
-
Si α<1/4, el bloque cruzará el origen y x2>0
será una posición de retorno
Supongamos que ocurre la primera situación x2>0,
tal como se muestra en la figura

-
Posición x3
El móvil parte de x2 con velocidad
inicial nula siempre que se cumpla que kx2≥ μmg,
k(x0-4αx0)≥
μmg o bien que α≤1/5, en caso contrario, la posición x3
será la final del bloque. Supongamos que se cumple la primera condición.
La ecuación del balance energético se escribe
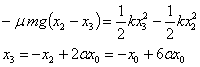
-
Si 1/6≤α≤1/5, el bloque no cruzará el origen
y x3≥0 será la posición final
-
Si α<1/6, el bloque cruzará el origen y x3<0
será una posición de retorno

Si
x3 está en el mismo lado que x2, x3
será la posición final del bloque.
En general.
En general, tendremos que
xn=(-1)n(1-2nα)x0
-
Si 1/(2n)≤α≤1/(2n-1), el bloque
no cruzará el origen y xn será la posición final
-
Si α<1/(2n), el bloque cruzará el
origen y xn será una posición de retorno
Dado el valor de α, el bloque se detiene en la
posición xn tal que
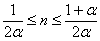
Ejemplo:
El parámetro
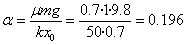
Calculamos la posición x1
x1=-x0+2αx0=-0.7+2·0.1372·0.7=-0.4256
que está a la izquierda del origen.
Calculamos la posición x2
x2=x0-4αx0=0.1512
que está a la derecha del origen.
Calculamos la posición x3
x3=-x0+6αx0=0.1232
Como x3 está a la derecha del
origen, es la posición final del bloque en reposo
Como podemos comprobar
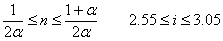
se cumple para n=3.
El espacio recorrido por el bloque hasta que se para en
la posición x3 es
s3=x0+2|x1|+2x2+|x3|
= x0+2(x0-2αx0)+2(x0-4αx0)+(x0-6αx0)
En general,
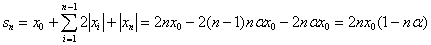
ya que la suma de n-1 números pares es (n-1)n
El trabajo de la fuerza de rozamiento es
Wr=-μmg·sn=-
μmg (1-nα)·(2n·x0)
La variación de energía potencial del bloque unido al
muelle es
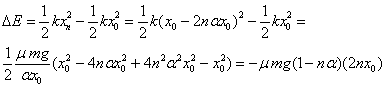
Ambas cantidades coinciden
Wr=ΔE
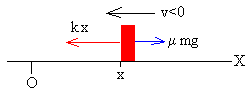 |
Cuando el bloque se mueve hacia la izquierda (v<0),
la ecuación del movimiento es
ma=-kx+ μmg,
|
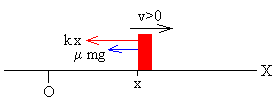 |
Cuando el bloque se mueve hacia la derecha (v>0),
la ecuación del movimiento es
ma=-kx- μmg,
|
Escribimos las ecuaciones del movimiento en forma de
ecuación diferencial
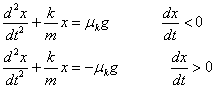
Las ecuaciones del movimiento nos recuerdan la
ecuación
diferencial de un MAS, pero además tiene un término adicional ±μkg
La solución de la ecuación diferencial es la suma de la
homogénea (la ecuación de un MAS) más una constante C. Introduciendo la solución particular (la constante C)
en la ecuación diferencial
(k/m)C=±μkg,
C=±μkmg/k=±αx0
La solución completa de cada una de las ecuaciones
diferenciales es
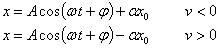
como puede comprobarse por simple sustitución
La velocidad del bloque es en ambos casos es
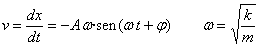
Las constantes A y φ
se determina a partir de las condiciones iniciales
-
Posición de partida x0
El bloque se mueve hacia la izquierda (v<0) si
la fuerza que ejerce el muelle kx0 es superior a la de
rozamiento μmg. En caso contrario, el bloque permanece en reposo
Supongamos que se cumple kx0≥
μmg.
Las condiciones iniciales son: en el instante t=0,
la velocidad v=0, y la posición es x=x0.
x0=A1cosφ+αx0
0=A1ω·senφ
La posición del bloque en función del tiempo se
escribe
x=A1cos(ωt)+αx0,
la amplitud es A1=x0-αx0.
x=(x0-αx0)cos(ωt)+αx0
El bloque se para momentáneamente en la posición x1
cuando v=0
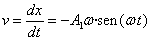
La velocidad se anula en el instante t, cuando
ωt=π. La posición del bloque en este instante es
x1=-(x0-αx0)+αx0
=-x0+2αx0
que es el mismo resultado que hemos obtenido en el
apartado anterior
-
Movimiento hacia la derecha v>0
El bloque se mueve hacia la derecha (v>0)
siempre que se cumpla que k|x1|≥ μmg . En caso
contrario, el bloque permanece en reposo. Supongamos que se cumple esta
condición
Las condiciones iniciales son: en el instante ωt=π,
la velocidad v=0, y la posición es x1.
x1=A2cos(π+φ)-αx0
0=A2ω·sen(π+φ)
La posición del bloque en función del tiempo se escribe
x=A2cos(ωt)-αx0,
la amplitud es A2=-x1-αx0=x0-3αx0
x=(x0-3αx0)cos(ωt)-αx0
El bloque se para momentáneamente en la posición x2
cuando v=0
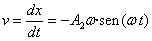
La velocidad se anula en el instante t, cuando
ωt=2π. La posición del bloque en este instante es
x2=A2-αx0
=x0-4αx0
que es el mismo resultado que hemos obtenido en el
apartado anterior
Se continúa el proceso hasta que el bloque se detiene
El bloque tarda el mismo tiempo en describir cada
una de las oscilaciones. Su
periodo es
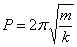
x=(x0-αx0)cos(ωt)+αx0, .
x=(x0-3αx0)cos(ωt)-αx0
x=x0(1-(2n-1)α)cos(ωt)-(-1)nαx0
v=-x0(1-(2n-1)α)ωsen(ωt)
 |
El bloque describe un MAS cuya amplitud permanece
constante durante cada semiperiodo de la oscilación.
La amplitud disminuye una cantidad constante 2αx0
entre dos semiperiodos consecutivos.
Los desplazamientos se sitúan entre un par de líneas
rectas con pendiente ±4αx0/P (lo que puede compararse con las envolventes
exponenciales en el caso del rozamiento viscoso)
La velocidad del bloque se hace cero en los instantes tn=n·π/ω
n=1, 2, 3,..
|
Ejemplo:
La frecuencia angular ω=7.07 rad/s, y el periodo
P=0.89 s
-
Verificamos que el bloque no permanece en reposo
kx0≥ μmg, 50·0.7>0.8·1·9.8
La amplitud de la primera semioscilación es A1=x0-αx0
=0.5628
El bloque se mueve hacia la izquierda (v<0).
La posición del bloque en función del tiempo t es
x=0.5628·cos(7.07·t)+0.1372
La velocidad del bloque es
v=-0.5628·7.07·sen(7.07·t)
La velocidad se hace nuevamente cero, en el instante
ωt=π, t=0.44
Calculamos la posición x1 en este
instante, x1=-0.5628+0.1372=-0.4256
que está a la izquierda del origen.
-
Verificamos que k|x1|≥ μmg,
50·0.4256>0.7·1·9.8, el bloque se mueve hacia la derecha
La amplitud de la segunda semioscilación es
A2=A1-2αx0
=0.2884
El bloque se mueve hacia la derecha (v>0). La
posición del bloque en función del tiempo t es
x=0.2884·cos(7.07·t)-0.1372
La velocidad del bloque es
v=-0.2884·7.07·sen(7.07·t)
La velocidad se hace nuevamente cero, en el instante
ωt=2π, t=0.89
Calculamos la posición x2 en este
instante, x2=0.2884-0.1372=0.1512
que está a la derecha del origen.
-
Verificamos que kx2≥ μmg,
50·0.1512>0.7·1·9.8. El bloque se mueve hacia la izquierda (v<0)
La amplitud de la tercera semioscilación es
A3=A2-2αx0=0.014
El bloque se mueve hacia la izquierda (v<0).
La posición del bloque en función del tiempo t es
x=0.014·cos(7.07·t)+0.1372
La velocidad del bloque es
v=-0.014·7.07·sen(7.07·t)
La velocidad se hace nuevamente cero, en el instante
ωt=3π, t=1.33
Calculamos la posición x3 en este
instante, x3=-0.014+0.1372=0.1232
que está a la derecha del origen.
Como x3 está a la derecha del
origen, es la posición final del bloque en reposo
Se introduce
-
El coeficiente de rozamiento μ
actuando en la barra de desplazamiento titulada Coef. rozamiento
-
La constante elástica k del
muelle o cuadrado de la frecuencia angular ω,
en el control de edición titulado Constante muelle.
-
La masa del bloque se ha fijado en m=1.0 kg
Se pulsa el botón titulado Inicio
Se pulsa el botón titulado Empieza
Se observa el movimiento del bloque entre los puntos de
retorno, hasta que se para.
Se representa la posición del bloque en función del
tiempo.
-
Una flecha de color rojo, representa la fuerza que
ejerce el muelle
-
Una flecha de color azul, representa la fuerza de
rozamiento.
En la parte superior derecha del applet, se
proporcionan los datos de
En la parte izquierda del applet, se representa la
energía del bloque en forma de diagrama de barras.
-
En color rojo, la energía potencial elástica
-
En color azul, la energía cinética
vemos como la energía total disminuye continuamente a
causa del trabajo de las fuerzas de rozamiento.
Se sugiere al lector que calcule los puntos de retorno
en un caso concreto y los compare con los proporcionados con el programa
interactivo, siguiendo los pasos de los ejemplos..
|