Movimiento Ondulatorio Armónico

1.-La expresión de una onda armónica que se propaga por una cuerda es:

$Ψ (x, t) = 1.25 \sin (0.25 π + 500 π t)$

Ψ en cm, x en m, t en segundos.

¿Cuál es la dirección y sentido de la propagación?
Calcula: la amplitud, longitud de onda, frecuencia, frecuencia angular, número de onda, periodo y la velocidad de propagación de la onda.
Calcula la velocidad y la aceleración máximas de un punto x de la cuerda

Ecuación de una onda

$\begin{array}{l} Ψ (x, t) = Ψ_{0} \sin k (x + v t) \\ Ψ (x, t) = 0.0125 \sin 0.25 π (x + 2000 t) \end{array}$

Se trata de una onda armónica que se propaga a lo largo del eje X hacia la izquierda (signo +), con velocidad v=2000 m/s.

Número de onda, k=0.25π m^-1
Longitud de onda, λ=2π/k=8 m
Periodo, λ=v·P, P=0.004 s
Frecuencia angular, ω=2π/P=500π rad/s
Frecuencia, f=1/P=250 Hz

Velocidad y acelaración de una partícula x del medio

$\begin{array}{l} \frac{\partial Ψ}{\partial t} = 0.0125 \cdot 500 π \cos (0.25 π x + 500 π t) \\ \frac{\partial^{2} Ψ}{\partial t^{2}} = - 0.0125 \cdot {(500 π)}^{2} \sin (0.25 π x + 500 π t) \end{array}$

Valores máximos

$\begin{array}{l} {(\frac{\partial Ψ}{\partial t})}_{m á x} = 6.25 π m/s \\ {(\frac{\partial^{2} Ψ}{\partial t^{2}})}_{m á x} = 3125 π^{2} {m/s}^{2} \end{array}$

2.-La ecuación Ψ=0.1sin(3x+2t) m, describe una onda armónica de amplitud Ψ₀= que se propaga a lo largo del eje X hacia la.... , con velocidad v= , su longitud de onda es λ= y su frecuencia es f= .

Una partícula del medio situada en x=π/3 describe un movimiento.... de amplitud.... y frecuencia angular ω= . La expresión de su velocidad es...

Solución

3.-Dos ondas armónicas que tienen la misma frecuencia, se propagan a lo largo del eje X hacia la derecha. La primera tiene una amplitud de 6 cm, la segunda de 8 cm, la diferencia de fase es π/2. Determinar la amplitud y fase de la onda armónica resultante

Solución

4.-La intensidad de la radiación solar media medida en la órbita de la Tierra es de 1367 W/m². Sabiendo que el radio de la órbita de la Tierra (supuesta circular) es de 1 UA=149.6·10⁹ m. Determinar

La intensidad de la radiación en la superficie del Sol cuyo radio es 6.96·10⁸ m
La intensidad de la radiación en la superficie de Marte cuya órbita, supuesta circular, tiene un radio de 1.524 UA

Solución

5.-Una barra de aluminio Y=7 10¹⁰N/m², densidad ρ=2.7 g/cm³ y sección 5 cm², transmite un movimiento ondulatorio armónico producido por una fuente de 100 Hz de frecuencia y 20 W de potencia. Calcular:

La velocidad de propagación y la longitud de onda.
La ecuación de la onda armónica.

Solución

$\begin{array}{l} v = \sqrt{\frac{Y}{ρ}} = \sqrt{\frac{7 \cdot 10^{10}}{2700}} = 5091.7 m/s \\ λ = v \cdot P = \frac{v}{f} = \frac{5091.7}{100} = 50.92 m \\ ω = \frac{2 π}{P} = 2 π f = 200 π rad/s \\ k = \frac{2 π}{λ} = 0.123 m^{-1} \end{array}$

Intensidad de la onda,

$I = \frac{20}{5 \cdot 10^{- 4}} = v (\frac{1}{2} ρ ω^{2} Ψ_{0}^{2}) Ψ_{0} = 1.21 \cdot 10^{- 4} m$

Ecuación de la onda armónica

$\begin{array}{l} Ψ (x, t) = Ψ_{0} \sin k (x - v t) \\ Ψ (x, t) = 1.21 \cdot 10^{- 4} \sin 0.123 (x - 5091.7 t) m \end{array}$

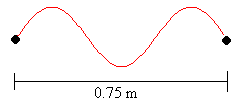
6.-Una cuerda de 75 cm de longitud y de 20 g/m de densidad lineal está sujeta por uno de sus extremos y por el otro está unida a una fuente vibrante de 80 Hz. Sabiendo que a esa frecuencia le corresponde el tercer armónico. Calcular:

la velocidad de propagación de las ondas transversales en la cuerda
la tensión de la misma.

Solución