Movimiento ondulatorio armónico

Ψ(x,t)=Ψ₀·sin k(x-vt)

Ψ(x,t)=Ψ₀·sin(kx-ωt)

• Amplitud, Ψ₀
• Velocidad de propagación, v
• Número de onda, k
• Longitud de onda, λ=2π/k
• Periodo, λ=v·P
• Frecuencia, f=1/P
• Frecuencia angular, ω=2π/P=kv
• La onda armónica se propaga a lo largo del eje X, hacia la derecha (signo -)

Ondas transversales en una cuerda

${\displaystyle v=\sqrt{\frac{T}{m}}}$

•   T  es la tensión de la cuerda en N
•   m  es la densidad lineal en kg/m

Ondas longitudinales en una barra elástica

${\displaystyle v=\sqrt{\frac{Y}{\rho }}}$

• Y es el módulo de la elasticidad del material o módulo de Young (expresado en N/m²)
• ρ es la densidad (expresada en kg/m³).

Intensidad del movimiento ondulatorio

es la energía transportada por unidad de área y por unidad de tiempo. Para un movimiento ondulatorio armónico de frecuencia angular ω y de amplitud Ψ₀ que se propaga en un medio de densidad ρ con velocidad v.

${\displaystyle I=v\left(\frac{1}{2}\rho {\omega }^2{\Psi }_0^2\right)}$

La unidad de medida es W/m².

La intensidad del movimiento ondulatorio a una distancia r de la fuente emisora puntual que emite en todas las direcciones de forma isótropa es.

${\displaystyle I=\frac{P}{4\pi r^2}}$

Siendo P la potencia de la fuente emisora.

Interferencia de las ondas producidas por dos fuentes sincrónicas

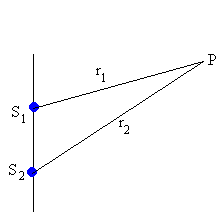
• Interferencia constructiva, r₂-r₁ =nλ
• Interferencia destructiva, r₂-r₁ =(n+½)λ