Desviación hacia el este de un cuerpo que cae (II)

En la página anterior "Desviación hacia el este de un cuerpo que cae (I)", hemos supuesto que la fuerza de atracción entre el cuerpo y la Tierra es central y conservativa, por lo que el cuerpo que cae describe una elipse para el observador inercial. Hemos determinado la ecuación de dicha trayectoria y su intersección con la superficie terrestre. El cálculo como hemos visto es bastante laborioso.

En esta página, vamos a obtener la fórmula de la desviación hacia el este de un cuerpo que cae desde una altura h, suponiendo, de nuevo, que el cuerpo está situado a una altura h sobre la superficie de un planeta de radio R en su plano ecuatorial, y que gira con velocidad angular constante ω alrededor del eje que pasa por sus polos.

El cuerpo está inicialmente en reposo a una altura h para el observador terrestre (no inercial), pero está situado a una distancia R+h del centro de la Tierra y lleva una velocidad (h+R)·ω respecto al sistema de referencia fijo (inercial), describiendo una órbita elíptica que interseca la superficie del planeta en un punto P. A la vez que el cuerpo se mueve, el observador no inercial situado inicialmente debajo del cuerpo va describiendo un arco de circunferencia. El resultado es una desviación hacia el este de dicho cuerpo en relación al observador no inercial.

El cálculo de esta desviación se fundamenta en dos premisas:

Que la fuerza de atracción es central, por lo que el momento angular se mantiene constante.
Que la altura h es muy pequeña comparada con el R radio del planeta.

La explicación de esta desviación es mucho más evidente para los estudiantes que la que se hace de ordinario usando la fórmula de la aceleración de Coriolis en el sistema de referencia en rotación.

Desviación hacia el este en el Ecuador

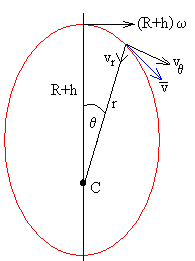coriolis7.gif (2680 bytes) Como vemos en la figura, el momento angular inicial de la partícula de masa m es

L=m(R+h)²ω

El momento angular en el instante t es

L=mrv_θ .

Siendo v_θ la componente r(dθ /dt) de la velocidad en coordenadas polares perpendicular a la dirección radial.

Como el momento angular se mantiene constante, tenemos la siguiente relación

$\frac{d θ}{d t} = ω \frac{{(R + h)}^{2}}{{(R + z)}^{2}} = ω \frac{{(1 + \frac{h}{R})}^{2}}{{(1 + \frac{z}{R})}^{2}}$

Siendo z la altura sobre la superficie del planeta r=R+z en el instante t.

Teniendo en cuenta que h y z son mucho menores que R, tenemos la siguiente relación aproximada más simple

$\frac{d θ}{d t} = ω \frac{{(1 + \frac{h}{R})}^{2}}{{(1 + \frac{z}{R})}^{2}} \approx ω (1 + \frac{2 h}{R}) (1 - \frac{2 z}{R}) \approx ω (1 + \frac{2 (h - z)}{R})$

Para poder integrar esta ecuación tenemos que buscar la dependencia de z con el tiempo t.

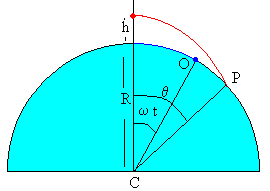coriolis6.gif (2641 bytes) Como z=h-gt²/2, donde g es la aceleración de la gravedad (supuesta constante) radialmente dirigida hacia el centro de la Tierra.

$\frac{d θ}{d t} = ω (1 + \frac{g t^{2}}{R}) θ = ω t + \frac{1}{3} \frac{ω}{R} g t^{3}$

Como vemos en la figura, el ángulo que forman el observador O y el objeto en la posición P sobre la superficie de la Tierra es la diferencia θ -ω t. Y el arco o distancia entre el punto O y el punto P es (arco=radio· ángulo)

$s = \frac{1}{3} g ω t^{3}$

Desviación hacia el este en un lugar de latitud λ , en el hemisferio Norte.

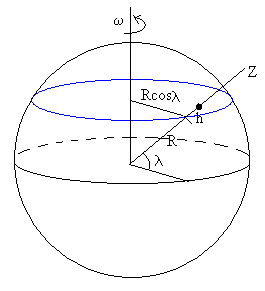coriolis8.gif (2842 bytes) Podemos generalizar este resultado para un objeto situado a una altura h sobre la superficie de la Tierra en un lugar de latitud λ .

Como vemos en la figura, dicho objeto, lleva una velocidad ω·(R+h)·cosλ , y tiene por tanto, un momento angular

L= ω (R+h)²cosλ

Los cálculos son similares a los ya efectuados basta sustituir ω por ω·cosλ

Para llegar a la fórmula de la desviación hacia el este

$s = \frac{1}{3} g ω t^{3} \cos λ$

La aceleración de la gravedad

Un tratamiento más exacto nos da un valor de g algo inferior al valor g₀ de la aceleración de la gravedad.

Para obtener z en función del tiempo tenemos que expresar la aceleración en coordenadas polares y considerar que la aceleración en la dirección radial a_r en el sistema de referencia inercial es -g₀, dirigida hacia el centro de la Tierra.

$a_{r} = \frac{d^{2} r}{d t^{2}} - r {(\frac{d θ}{d t})}^{2} = - g_{0}$

El término que disminuye g₀ es la aceleración centrífuga que es pequeña comparada con g₀. Como r=R+z. tenemos

$\frac{d^{2} z}{d t^{2}} = - g$

Integrando la ecuación diferencial de segundo orden para un móvil que parte de la altura z=h con velocidad inicial nula en la dirección radial tenemos que.

$z = h - \frac{1}{2} g t^{2}$

Referencias

Mohazzabi P. Free fall and angular momentum. Am. J. Phys. 67 (11) November 1999, pp. 1017-102