Ecuación de la trayectoria

En esta página, vamos a deducir paso a paso la ecuación de la trayectoria de una partícula bajo la acción de una fuerza inversamente proporcional al cuadrado de la distancia.

Las fuerza de interacción gravitatoria y eléctrica son centrales y conservativas. Por tanto, la energía y el momento angular se mantienen constantes en todos los puntos de la trayectoria

Posición y velocidad en coordenadas polares

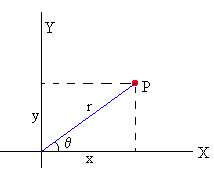
polar_1.gif (1689 bytes)

La posición del punto P es

x=r·cosθ
y=r·sinθ

Expresamos la velocidad de la partícula en coordenadas polares

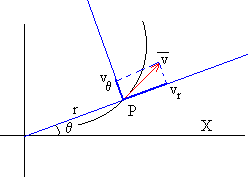
polar_2.gif (2122 bytes)

$v = \frac{d r}{d t} = \hat{r} \frac{d r}{d t} + r \frac{d \hat{r}}{d t}$

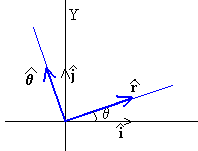Calculamos las componentes rectangulares de los vectores unitarios r y θ .

$\begin{array}{l} \hat{r} = \hat{i} \cos θ + \hat{j} \sin θ \\ \hat{θ} = - \hat{i} \sin θ + \hat{j} \cos θ \end{array}$

vemos que

$\frac{d \hat{r}}{d t} = - \hat{i} \sin θ \frac{d θ}{d t} + \hat{j} \cos θ \frac{d θ}{d t} = \hat{θ} \frac{d θ}{d t}$

Las componentes del vector velocidad en coordenadas polares son, por tanto

$v = \hat{r} \frac{d r}{d t} + \hat{θ} r \frac{d θ}{d t}$

La energía y el momento angular en coordenadas polares

La expresión de la energía en coordenadas polares es

$\begin{array}{l} E = \frac{1}{2} m v^{2} + \frac{k}{r} \\ E = \frac{1}{2} m {(\frac{d r}{d t})}^{2} + \frac{1}{2} m r^{2} {(\frac{d θ}{d t})}^{2} + \frac{k}{r} \end{array}$

Donde k/r es la energía potencial correspondiente a la fuerza conservativa F=k/r².

Con k=-GMm si la interacción es gravitatoria

$k = \frac{Q q}{4 π ε_{0}}$ si la interacción es de tipo eléctrico

k es negativo si la fuerza es atractiva
k es positivo si la fuerza es repulsiva

Expresamos el momento angular L en coordenadas polares

$L = r \times m v = m r \times (\hat{r} \frac{d r}{d t} + \hat{θ} r \frac{d θ}{d t}) = m r^{2} \frac{d θ}{d t} \hat{k}$

Despejamos dθ /dt en la expresión del momento angular y la introducimos en la expresión de la energía. Tenemos dos ecuaciones

$\begin{array}{l} E = \frac{1}{2} m {(\frac{d r}{d t})}^{2} + \frac{L^{2}}{2 m r^{2}} + \frac{k}{r} \\ L = m r^{2} \frac{d θ}{d t} \end{array}$

Ecuación de la trayectoria

Eliminamos dt entre estas dos ecuaciones para obtener la ecuación de la trayectoria

$\frac{d θ}{d r} = \frac{\frac{L}{m r^{2}}}{\sqrt{\frac{2}{m} (E - \frac{L^{2}}{2 m r^{2}} - \frac{k}{r})}}$

Para integrar se hace el cambio u=1/r

$θ = \frac{L}{\sqrt{2 m}} \int \frac{- d u}{\sqrt{E - \frac{L^{2}}{2 m} u^{2} - k u}}$

Tenemos una integral del tipo

$\begin{array}{l} \int \frac{- d u}{\sqrt{- a u^{2} - b u + c}} = \int \frac{- d u}{\sqrt{a [\frac{c}{a} + \frac{b^{2}}{4 a^{2}} - {(u + \frac{b}{2 a})}^{2}]}} \\ a = \frac{L^{2}}{2 m} b = k c = E \end{array}$

Hacemos el cambio

$\begin{array}{l} u + \frac{b}{2 a} = \sqrt{\frac{c}{a} + \frac{b^{2}}{4 a^{2}}} \cos t \\ θ = \frac{L}{\sqrt{2 m}} \frac{1}{\sqrt{a}} t θ = t \end{array}$

Ahora, vamos deshaciendo los cambios

$\frac{1}{r} + \frac{b}{2 a} = \sqrt{\frac{c}{a} + \frac{b^{2}}{4 a^{2}}} \cos θ$

Hay dos posibles soluciones según el signo de b o de k.

Si k o b es positivo

$r = \frac{\frac{L^{2}}{m k}}{- 1 + \sqrt{1 + \frac{2 E L^{2}}{m k^{2}}} \cos θ}$

Si k o b es negativo

$r = \frac{\frac{L^{2}}{m k}}{1 + \sqrt{1 + \frac{2 E L^{2}}{m k^{2}}} \cos θ}$

La ecuación de la trayectoria es

$\begin{array}{l} k > 0 r = \frac{d}{ε \cos θ - 1} \\ k < 0 r = \frac{d}{ε \cos θ + 1} \end{array}$

La primera, es la ecuación de una hipérbola en coordenadas polares
La segunda, es la ecuación de una cónica (elipse, parábola o hipérbola) dependiendo del valor de la excentricidad ε .

Tercera ley de Kepler

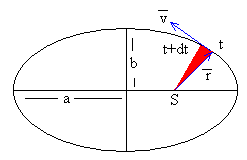kepler_a1.gif (2032 bytes) La figura muestra un planeta que está describiendo una órbita alrededor del centro fijo de fuerzas S. la posición del planeta en el instante t viene dada por el vector r

En un pequeño intervalo de tiempo el planeta se desplaza v·dt. El área barrida por el radio vector r entre los instantes t y t+dt es el área de un triángulo

$d A = \frac{1}{2} | r \times v \cdot d t |$

El momento angular del planeta es L=r×mv. Como la fuerza de atracción es central, el momento angular L permanece constante en módulo y dirección.

$\frac{d A}{d t} = \frac{L}{2 m}$

Mientras el radio vector barre el área de la elipse es A=π ab el planeta emplea un tiempo igual al periodo de revolución P. De modo que

P=2mπ ab/L

A partir de esta relación vamos a obtener la tercera ley de Kepler.

La fuerza de atracción es central

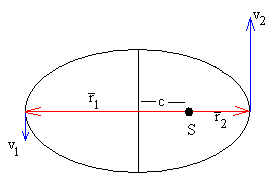kepler_a2.gif (2136 bytes) En la figura tenemos que el momento angular L en los puntos de máxima proximidad y máximo alejamiento del planeta valen, respectivamente, L=mr₂·v₂= mr₁·v₁.

La fuerza de atracción es conservativa

La energía total permanece constante en todos los puntos de la trayectoria.

$\frac{1}{2} m v_{1}^{2} - G \frac{M m}{r_{1}} = \frac{1}{2} m v_{2}^{2} - G \frac{M m}{r_{2}}$

Eliminado v₁ y v₂ en este par de ecuaciones tenemos

$\frac{L^{2}}{2 m} (r_{1} + r_{2}) = G M m \cdot r_{1} \cdot r_{2} L^{2} = \frac{G M m^{2}}{a} r_{1} \cdot r_{2}$

De la geometría de la elipse tenemos que

r₁=a+c
r₂=a-c

siendo c la semidistancia focal. La relación entre los semiejes mayor a y menor b de la elipse es a²-b²=c². Por lo que el producto r₁·r₂=b²

El módulo del momento angular L se expresa en términos de los semiejes a y b de la elipse

$L^{2} = G M m^{2} \frac{b^{2}}{a}$

Introduciendo el valor de L en la fórmula del periodo P obtenemos la tercera ley de Kepler.

$P^{2} = \frac{4 π^{2}}{G M} a^{3}$