Orbitas de la misma energía.

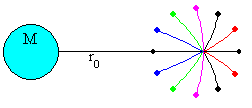Imaginemos un misil lanzado desde la superficie de la Tierra verticalmente, y que en el punto más alto de su trayectoria explota en varios fragmentos iguales que salen en todas las direcciones con igual velocidad.

El movimiento posterior de los fragmentos, se debe únicamente a la fuerza de atracción de la Tierra y por tanto, describirán órbitas elípticas si su energía total es negativa.

Descripción

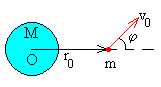El momento angular y la energía de un fragmento de masa m lanzado desde una distancia r₀ del centro de la Tierra, con velocidad v₀ haciendo un ángulo φ con el radio vector es

$\begin{array}{l} L = m r_{0} v_{0} sin ϕ \\ E = \frac{1}{2} m v_{0}^{2} - \frac{G M m}{r_{0}} \end{array}$

Todos los fragmentos tienen la misma energía E, pero distinto momento angular L

En una página previa, demostramos que el semieje mayor a es independiente del momento angular L, y solamente depende de la energía total E.

$a = - \frac{m G M}{2 E}$

Todos los fragmentos tienen el mismo semieje mayor a. Por la tercera ley de Kepler el periodo de todos los fragmentos será el mismo. Todos los fragmentos salen a la vez del mismo punto y regresan después de un tiempo igual al periodo al mismo punto.

Vamos a estudiar ahora los distintos casos que pueden presentarse dependiendo del ángulo de lanzamiento.

Cuando el ángulo φ=0

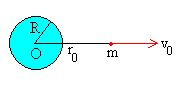El momento angular L=0, por lo que la trayectoria es una línea recta que pasa por el centro de fuerzas. El fragmento se eleva y luego cae hacia la Tierra a lo largo de la dirección radial.

La máxima distancia r a la que se aleja el fragmento, se calcula poniendo v=0 en la ecuación de constancia de la energía y a continuación, se despeja r.

$E = \frac{1}{2} m v_{0}^{2} - \frac{G M m}{r_{0}} = - \frac{G M m}{r}$

La velocidad v con la que impacta en la superficie de la Tierra, se obtiene poniendo r=R (radio de la Tierra) en la ecuación de la energía

$E = \frac{1}{2} m v_{0}^{2} - \frac{G M m}{r_{0}} = \frac{1}{2} m v^{2} - \frac{G M m}{R}$

Cuando el ángulo φ=180º

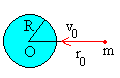El fragmento cae directamente hacia la superficie de la Tierra, alcanzando su superficie con la velocidad v calculada en el apartado anterior.

Cuando el ángulo φ=90º

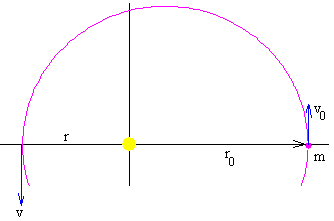El fragmento describe una elipse cuyo eje mayor es 2a=r+r₀. Aplicando la constancia del momento angular y de la energía.

$\begin{array}{l} m r v = m r_{0} v_{0} \\ \frac{1}{2} m v^{2} - \frac{G M m}{r} = \frac{1}{2} m v_{0}^{2} - \frac{G M m}{r_{0}} \end{array}$

Se resuelve el sistema de dos ecuaciones con dos incógnitas para calcular r y v.

Cuando el ángulo es φ

El fragmento describe una elipse cuyo eje mayor está girado con respecto del eje X.

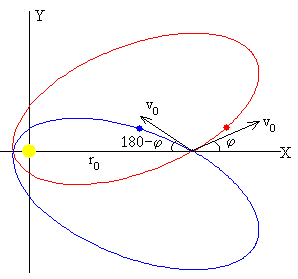
Los dos fragmentos cuyas velocidades forman con el radio vector ángulos φ y 180-φ, tienen el mismo momento angular y la misma energía. Sus trayectorias son simétricas respecto del eje X, tal como podemos ver en la figura.

Ejemplos

Para resolver estos ejemplos se adopta un Sistema de Unidades tal que GM=1

Supongamos que introducimos los siguientes valores

Posición, r₀=3.0
Velocidad, v₀=0.5

Cuando el ángulo es φ=0.

La distancia máxima que alcanza el fragmento en la dirección radial es

$\frac{1}{2} {0.5}^{2} - \frac{1.0}{3.0} = - \frac{1.0}{r} r = 4.8$

Cuando φ=90.

Primero, calculamos la velocidad de escape a la distancia r₀=3.0, que es

$v_{e}^{2} = \frac{2}{3}$

Después, calculamos la velocidad y la distancia máxima o mínima al centro de fuerzas

$v_{2} = \frac{2 / 3}{0.5} - 0.5 = 0.83 r_{2} = 3 \frac{{0.5}^{2}}{2 / 3 - {0.5}^{2}} = 1.8$

El eje mayor de la elipse es 2a= 3.0+1.8=4.8

Cuando el ángulo es φ=30.

El momento angular vale L=0.5·3·sin30º=0.75

La energía vale E=0.5²/2-1/3=-0.21

Calculamos la excentricidad ε de la elipse y el parámetro d

ε²=1-2·0.75²·0.21=0.77

d=0.75²=0.5625

La mínima distancia del fragmento al centro de fuerzas se produce cuando la posición angular θ=0º y la máxima cuando θ=180º

$\begin{array}{l} r_{\min} = \frac{d}{1 + ε} = \frac{0.5625}{1 + \sqrt{0.77}} = 0.3 \\ r_{m á x} = \frac{d}{1 - ε} = \frac{0.5625}{1 - \sqrt{0.77}} = 4.5 \end{array}$

El eje mayor de la elipse es 2a=r_min+r_máx=4.8

El eje mayor de la elipse se puede obtener de forma directa mediante la fórmula

$2 a = - \frac{m G M}{E} = \frac{1}{0.21} = 4.8$

El periodo de todos los fragmentos es

$P^{2} = \frac{4 π^{2} a^{3}}{G M} = \frac{4 π^{2} {2.4}^{3}}{1.0} P = 23.36$

Actividades

Se introduce

La velocidad v₀ del fragmento en el control de edición titulado Velocidad
La posición r₀ en el control de edición titulado Posición.

Se pulsa el botón titulado Empieza

No se aceptan valores de v₀ y r₀ que den lugar:

a una energía E positiva o nula.
a una trayectoria cuyo apogeo sea mayor de 6 unidades
a una trayectoria cuyo perigeo sea menor que 0.1 unidades

Si se cumple alguno de estos tres casos, el foco regresa al control de edición titulado Velocidad, para que el usuario cambie los valores de estos dos parámetros.

En el caso de que los dos valores sean aceptados, se observa las trayectorias de los fragmentos cuya velocidad forma ángulos de 30º, 60º, 90º, 120º y 150º con el radio vector.

Observamos que todas las trayectorias tienen el mismo eje mayor y por tanto, los fragmentos se vuelven a encontrar en el punto de partida transcurrido un periodo P.

KeplerApplet1 aparecerá en un explorador compatible con JDK 1.1.