Orbitas de la misma energía.

Ecuación de la trayectoria

Como se ha descrito en otras páginas, una partícula sometida a una fuerza central atractiva, inversamente proporcional al cuadrado de la distancia al centro de fuerzas, describe una trayectoria elíptica si su energía total E<0 es negativa,

$r = \frac{d}{1 + ε \cos θ}$

Los parámetros d y ε (excentricidad) están relacionados con el momento angular L y la energía E de la partícula

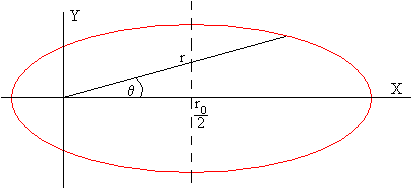
$d = \frac{L^{2}}{G M m^{2}} ε = \sqrt{1 + \frac{2 L^{2} E}{G^{2} M^{2} m^{3}}}$

En este apartado, vamos a determinar la ecuación de la elipse que describe una partícula que dista r₀ del centro de fuerzas, disparada con velocidad inicial v₀, haciendo un ángulo φ entre dicha velocidad y la línea que une el centro fuerzas y el punto de disparo, tal como se muestra en la figura.

Por ser la fuerza de atracción conservativa, la energía es constante en todos los puntos de la trayectoria y vale

$E = \frac{1}{2} m v_{0}^{2} - G \frac{M m}{r_{0}}$

Por ser la fuerza de atracción central, el momento angular es constante en todos los puntos de la trayectoria.

L=mr₀·v₀·sinφ

La ecuación de una elipse girada un ángulo θ_g es

$r = \frac{d}{1 + ε \cos (θ - θ_{g})}$

r y θ son las coordenadas polares de la partícula, la distancia al origen y el ángulo que forma el radio vector que une el centro de fuerzas y la partícula con el eje X, respectivamente.

θ_g es el ángulo que forma el eje mayor de la elipse con el eje X, que se calcula del siguiente modo: cuando θ=0, r=r₀

$\cos (- θ_{g}) = \frac{d - r_{0}}{ε r_{0}}$

Conocida la energía E y del momento angular L, determinamos los valores de los parámetros d y ε de la elipse.

$d = \frac{r_{0}^{2} v_{0}^{2} {sin}^{2} ϕ}{G M} ε = \sqrt{1 + \frac{2 r_{0}^{2} v_{0}^{2} {sin}^{2} ϕ (\frac{1}{2} v_{0}^{2} - G M / r_{0})}{G^{2} M^{2}}}$

Definimos el parámetro adimensional

$A = \frac{2 G M}{r_{0} v_{0}^{2}}$

En función de este parámetro

$d = \frac{2 r_{0} {sin}^{2} ϕ}{A} ε = \sqrt{1 - \frac{4 {sin}^{2} ϕ}{A^{2}} (A - 1)}$

A medida que el ángulo de disparo cambia, 0<φ<π, la excentricidad de la elipse varía

La excentricidad es máxima ε=1, cuando φ=0
La excentricidad es mínima ε=(A-2)/A, cuando φ=π/2

Como caso particular mencionaremos, que cuando A=2, o cuando la velocidad de disparo es

$v_{0} = \sqrt{\frac{G M}{r_{0}}}$

la trayectoria es una circunferencia, ε=0, de radio r₀.

La ecuación de la elipse girada un ángulo θ_g es

$\begin{array}{l} r = \frac{d}{1 + ε (\cos θ \cdot \cos θ_{g} + sin θ \cdot sin θ_{g})} = \frac{d}{1 + ε (\cos θ \cdot \frac{d - r_{0}}{ε r_{0}} + sin θ \cdot \sqrt{1 - {(\frac{d - r_{0}}{ε r_{0}})}^{2}})} \\ r = \frac{d}{1 + (\frac{d}{r_{0}} - 1) \cos θ + \sqrt{ε^{2} - {(\frac{d}{r_{0}} - 1)}^{2}} sin θ} = \frac{2 r_{0} {sin}^{2} ϕ / A}{1 + (\frac{2 {sin}^{2} ϕ}{A} - 1) \cos θ + \frac{2 sin ϕ \cos ϕ}{A} sin θ} \end{array}$

Simplificando, llegamos a la ecuación

$\frac{r_{0}}{r} = \frac{A (1 - \cos θ)}{2 {sin}^{2} ϕ} + \cos θ + \frac{sin θ}{\tan ϕ}$

La ecuación de la trayectoria depende del ángulo φ con el que se dispara la partícula.
f(r, θ, φ)=0

Envolvente de las elipses

La ecuación de la envolvente de las trayectorias elípticas se obtiene derivando con respecto a φ e igualando a cero.

$\frac{\partial f}{\partial ϕ} = 0$

y combinando ésta con la ecuación de la trayectoria para eliminar el ángulo φ

$A (1 - \cos θ) \frac{- 2 sin ϕ \cos ϕ}{{2sin}^{4} ϕ} - \frac{sin θ / \cos^{2} ϕ}{\tan^{2} ϕ} = 0$

Simplificando llegamos a la expresión

$\begin{array}{l} A (1 - \cos θ) \cos ϕ + sin ϕ \cdot sin θ = 0 \\ \tan ϕ = - \frac{A (1 - \cos θ)}{sin θ} \end{array}$

Introducimos esta expresión en la ecuación de la elipse, teniendo en cuenta la relación trigonométrica

${sin}^{2} ϕ = \frac{\tan^{2} ϕ}{1 + \tan^{2} ϕ}$

realizando algunas operaciones

$\begin{array}{l} \frac{r_{0}}{r} = \frac{1}{2} \frac{{sin}^{2} θ + A^{2} {(1 - \cos θ)}^{2}}{2 A (1 - \cos θ)} + \cos θ - \frac{{sin}^{2} θ}{A (1 - \cos θ)} \\ \frac{r_{0}}{r} = \frac{1}{2} \frac{A^{2} (1 - \cos θ) - (1 + \cos θ)}{A} + \cos θ \\ \frac{r_{0}}{r} = \frac{1}{2} {(A - \frac{1}{A}) - (A + \frac{1}{A} - 2) \cos θ} \\ \frac{r_{0}}{r} = \frac{1}{2} {(A - \frac{1}{A}) - {(\sqrt{A} - \frac{1}{\sqrt{A}})}^{2} \cos θ} \end{array}$

y despejando r, obtenemos la ecuación de la elipse

$r = \frac{2 r_{0}}{(A - \frac{1}{A}) - {(\sqrt{A} - \frac{1}{\sqrt{A}})}^{2} \cos θ}$

Calculamos el semieje mayor a y el semieje menor b de la elipse

$\begin{array}{l} θ = 0 r_{1} = r_{0} \frac{A}{A - 1} \\ θ = π r_{2} = r_{0} \frac{1}{A - 1} \\ a = \frac{r_{1} + r_{2}}{2} = \frac{r_{0}}{2} \frac{A + 1}{A - 1} \\ c = a - r_{2} = \frac{r_{0}}{2} \\ b = \sqrt{a^{2} - c^{2}} = r_{0} \frac{\sqrt{A}}{A - 1} \end{array}$

La ecuación de la elipse en coordenadas rectangulares es

$\frac{{(x - r_{0} / 2)}^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 A = \frac{2 G M}{r_{0} v_{0}^{2}}$

Actividades

Se introduce el valor del parámetro A, actuando en la barra de desplazamiento titulada Parámetro

Se pulsa el botón titulado Dibuja

Se dibuja las trayectorias elípticas de las partículas disparadas con ángulos φ=30º, 60º, 90º, 120º, 150º. Se dibuja también la envolvente de dichas elipses.

KeplerApplet1 aparecerá en un explorador compatible con JDK 1.1.

Referencias

Butikov E. Families of Keplerian orbits. Eur. J. Phys. 24 (2003) pp. 175-183

Laporte O., On Kepler ellipses starting from a point of space. Am. J. Phys. 38 (7) July 1970, pp. 837-840