Deducción de la fórmula de la aceleración normal

En esta página, se describen las deducciones más simples de la fórmula de la aceleración normal para un movimiento circular uniforme que se han encontrado

Deducción (I)

Supongamos que el cuerpo describe un movimiento circular de radio r con velocidad constante v.

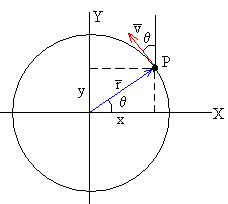
El vector velocidad v es tangente a la trayectoria y es perpendicular al vector posición r.

Las componentes rectangulares del vector velocidad v son

$\begin{array}{l} v_{x} = - v \sin θ = - v \frac{y}{r} \\ v_{y} = v cos θ = v \frac{x}{r} \end{array}$

Como v/r es constante, las componentes del vector aceleración a son

$\begin{array}{l} a_{x} = \frac{d v_{x}}{d t} = - \frac{v}{r} \frac{d y}{d t} = - \frac{v}{r} v_{y} = - \frac{v^{2}}{r} cos θ \\ a_{y} = \frac{d v_{y}}{d t} = \frac{v}{r} \frac{d x}{d t} = \frac{v}{r} v_{x} = - \frac{v^{2}}{r} \sin θ \end{array}$

El módulo de la aceleración a en el movimiento circular uniforme es

$a = \sqrt{a_{x}^{2} + a_{y}^{2}} = \frac{v^{2}}{r}$

Su dirección es radial (la misma que el vector r) y su sentido es hacia el centro (de sentido contrario al vector r).

Deducción (II)

En esta sección, se describe la deducción más simple que se ha encontrado de la fórmula de la aceleración normal en un movimiento circular uniforme

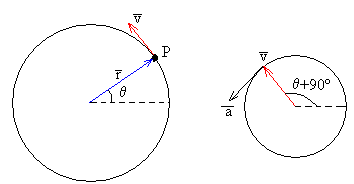
El vector velocidad v se define

$v = \frac{d r}{d t}$

Su módulo para un movimiento circular uniforme es

$v = \frac{2 π r}{P}$

Siendo P el periodo o tiempo que tarda en completar una vuelta

Su dirección es tangente a la trayectoria, es decir, perpendicular al vector r

El vector aceleración a se define

$a = \frac{d v}{d t}$

El vector aceleración a se obtiene a partir del vector velocidad v, de la misma manera que el vector velocidad v se obtiene a partir del vector posición r. Su módulo será, análogamente,

$a = \frac{2 π v}{P} = \frac{v}{r} v = \frac{v^{2}}{r}$

Su dirección es tangente a la circunferencia de radio v, es decir perpendicular al vector v. Como vemos en la figura, los vectores a y r tienen la misma dirección pero sentidos contrarios.