Alcance máximo en el plano horizontal

Hemos demostrado que el alcance máximo se obtiene para el ángulo de tiro de 45º, cuando el cañón y el blanco están en una superficie horizontal.

En esta página, vamos a estudiar el movimiento de un proyectil que se dispara desde una altura h sobre una superficie horizontal, y a calcular el ángulo de tiro para el cual el alcance es máximo.

Este ejemplo, nos permiten estudiar en detalle la trayectoria parabólica y practicar con funciones trigonométricas seno, coseno y tangente.

Se dispara un proyectil desde una cierta altura sobre el suelo

Se dispara un proyectil desde una altura h sobre un plano horizontal con velocidad inicial v₀, haciendo un ángulo θ con la horizontal. Para describir el movimiento establecemos un sistema de referencia como se indica en la figura.

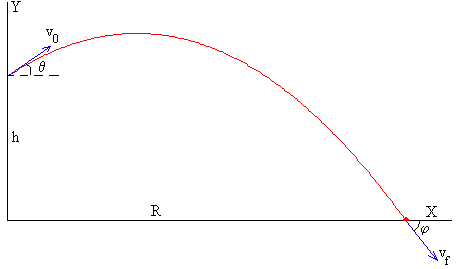
Las componentes de la velocidad del proyectil en función del tiempo son:

v_x=v₀·cosθ
v_y=v₀·sinθ-g·t

La posición del proyectil en función del tiempo es

x= v₀·cosθ·t
y= h+v₀·sinθ·t-g·t²/2

Estas son las ecuaciones paramétricas de la trayectoria, ya que dado el tiempo t, se obtiene la posición x e y del proyectil.

El tiempo de vuelo T se obtiene poniendo y=0 en la segunda ecuación y despejando el tiempo t.

$T = \frac{v_{0}}{g} (sin θ + \sqrt{{sin}^{2} θ + 2 z}) z = \frac{g h}{v_{0}^{2}}$

El proyectil llega al punto de impacto en el instante t=T. Sustituyendo t en la primera ecuación obtenemos el alcance, o distancia horizontal entre el origen y el punto de impacto, R.

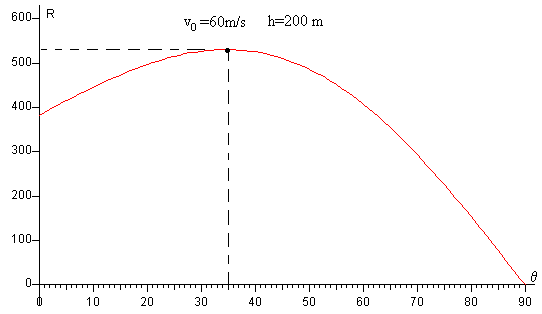
$R = \frac{v_{0}^{2}}{g} (sin θ + \sqrt{{sin}^{2} θ + 2 z}) \cos θ z = \frac{g h}{v_{0}^{2}}$

En la figura, se representa el alcance R en función del ángulo de tiro θ.

La componente v_y de la velocidad cuando el cuerpo llega al suelo es

$v_{y} = v_{0} sin θ - g T = - v_{0} \sqrt{{sin}^{2} θ + 2 z}$

La velocidad final v_f del proyectil cuando llega al suelo y el ángulo que forma con la horizontal (véase la primera figura) es

$\begin{array}{l} v_{f} = \sqrt{v_{x}^{2} + v_{y}^{2}} = v_{0} \sqrt{1 + 2 z} \\ \tan ϕ = \frac{v_{y}}{v_{x}} = - \frac{\sqrt{{sin}^{2} θ + 2 z}}{\cos θ} \end{array}$

El módulo de la velocidad final v_f se puede calcular también, aplicando el principio de conservación de la energía.

$\frac{1}{2} m v_{0}^{2} + m g h = \frac{1}{2} m v_{f}^{2}$

Alcance máximo

Derivando R con respecto del ángulo de tiro θ e igualando a cero obtenemos el ángulo de tiro θ_m para el cual el alcance es máximo.

$\begin{array}{l} (\cos θ + \frac{2 sin θ \cos θ}{2 \sqrt{{sin}^{2} θ + 2 z}}) \cos θ - (sin θ + \sqrt{{sin}^{2} θ + 2 z}) sin θ = 0 \\ (\cos^{2} θ - {sin}^{2} θ) (sin θ + \sqrt{{sin}^{2} θ + 2 z}) = 2 z sin θ \\ \sqrt{{sin}^{2} θ + 2 z} = \frac{2 z sin θ}{\cos (2 θ)} - sin θ \end{array}$

Elevamos al cuadrado y simplificamos

${(1 - 2 \cdot \sin^{2} θ)}^{2} = 2 z \cdot {sin}^{2} θ - 2 \cdot {sin}^{2} θ (1 - 2 \cdot {sin}^{2} θ)$

${cos}^{2} θ = \frac{1 + 2 z}{2 + 2 z} {sin}^{2} θ = \frac{1}{2 + 2 z}$

El ángulo θ_m para el cual el alcance R es máximo vale

$\tan θ_{m} = \frac{1}{\sqrt{1 + 2 z}} = \frac{v_{0}}{\sqrt{v_{0}^{2} + 2 g h}}$

Sustituyendo cosθ y sinθ en función del parámetro z, en la expresión del alcance R, se obtiene después de algunas operaciones

$R_{m} = \frac{v_{0}^{2}}{g} \sqrt{1 + 2 z} = \frac{v_{0}}{g} \sqrt{v_{0}^{2} + 2 g h}$

Otra forma de expresar el alcance máximo R_m es

$R_{m} = \frac{v_{0}^{2}}{g \cdot \tan θ_{m}}$

Teniendo en cuenta la relación trigonométrica

$R_{m} = \frac{v_{0}^{2}}{g \cdot \tan θ_{m}}$

llegamos a esta expresión tan simple para el alcance máximo

R_m=h·tan(2θ_m)

El tiempo de vuelo T_m para el ángulo θ_m

$T_{m} = \frac{v_{0}}{g} \sqrt{2 + 2 z} = \frac{\sqrt{2 (v_{0}^{2} + 2 g h)}}{g}$

El alcance máximo sin cálculo de derivadas

Una forma alternativa de calcular el ángulo θ_m, sin tener que realizar un cálculo de derivadas es el siguiente:

Eliminamos el tiempo t, en de las ecuaciones paramétricas de la trayectoria, llegamos a la ecuación de la parábola (recuérdese que 1/cos²θ=1+tan²θ)

$y = x \tan θ - \frac{g x^{2}}{2 v_{0}^{2}} (1 + \tan^{2} θ)$

En el punto de impacto con el suelo y=0, obtenemos la ecuación de segundo grado en tanθ

$\frac{g R^{2}}{2 v_{0}^{2}} \tan^{2} θ - R \cdot \tan θ + (\frac{g R^{2}}{2 v_{0}^{2}} - h) = 0$

con dos soluciones para R<R_m, y una solución para R=R_m y ninguna para R>R_m,véase la figura.

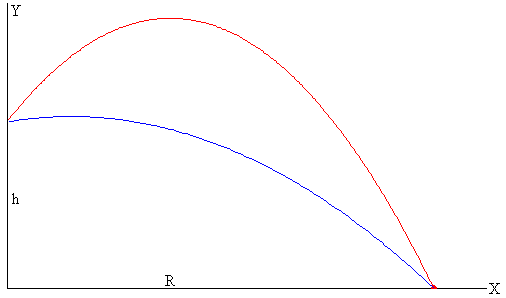
Esto implica que el discriminante de la ecuación de segundo grado debe ser cero para el ángulo θ_m que hace que el alcance sea máximo

$R_{m}^{2} - 4 \frac{g R_{m}^{2}}{2 v_{0}^{2}} (\frac{g R_{m}^{2}}{2 v_{0}^{2}} - h) = 0 R_{m} = \frac{v_{0}}{g} \sqrt{2 g h + v_{0}^{2}}$

El mismo resultado que ya obtuvimos de una forma más laboriosa.

Velocidad final y velocidad inicial

La velocidad final y el ángulo que forma con el eje X son

$\begin{array}{l} v_{f} = v_{0} \sqrt{1 + 2 z} \\ \tan ϕ_{m} = - \frac{\sqrt{{sin}^{2} θ + 2 z}}{\cos θ} = - \sqrt{1 + 2 z} \end{array}$

La relación entre el ángulo de disparo θ_m y el ángulo φ_m que forma el vector velocidad cuando el proyectil llega al suelo es

$\tan ϕ_{m} = - \frac{1}{\tan θ_{m}} θ_{m} = ϕ_{m} + \frac{π}{2}$

El vector velocidad inicial v₀ y el vector velocidad final v_f son perpendiculares,

Ejemplo:

La velocidad de disparo v₀=60 m/s,
La altura inicial del proyectil h=200 m
El ángulo de tiro θ=30º.

El alcance R es

$z = \frac{9.8 \cdot 200}{60^{2}} = 0. 54 R = \frac{60^{2}}{9.8} (sin30º + \sqrt{{sin}^{2} 30 º + 2 \cdot 0.54}) \cos 30 º = 527.2 m$

El tiempo T de vuelo del proyectil es

$T = \frac{60}{9.8} (sin30º + \sqrt{{sin}^{2} 30 º + 2 \cdot 0.54}) = 10 .1 s$

El alcance máximo (véase la última figura) se obtiene para el ángulo

$\tan θ_{m} = \frac{1}{\sqrt{1 + 2 \cdot 0.54}} θ_{m} = 34.7 º$

El alcance y el tiempo de vuelo para este ángulo son, respectivamente

$\begin{array}{l} R_{m} = \frac{60^{2}}{9.8} \sqrt{1 + 2 \cdot 0.54} = 530.9 m \\ T_{m} = \frac{60}{9.8} \sqrt{2 + 2 \cdot 0.54} = 10.8 s \end{array}$

Ángulos de tiro que producen el mismo alcance R=450 m.

Podemos calcular los dos ángulos de tiro que producen el mismo alcance R<R_m, por ejemplo un alcance de R=450 m. Calculamos las raíces de la ecuación de segundo grado en tanθ

$\frac{9.8 \cdot 450^{2}}{2 \cdot 60^{2}} \tan^{2} θ - 450 \cdot \tan θ + (\frac{9.8 \cdot 450^{2}}{2 \cdot 60^{2}} - 200) = 0$

θ₁=10.8º, θ₂=55.3º, Como vemos θ₁<θ_m<θ₂

Supongamos que un atleta lanza un peso desde una altura h con una velocidad v₀, haciendo un ángulo θ con la horizontal.

Si el atleta lanza el peso desde una altura de h=2.1 m y quiere que llegue a una distancia R_m=22 m, el ángulo óptimo de lanzamiento θ_m vale

R_m=h·tan(2θ_m) θ_m=42.3º

El análisis del lanzamiento del peso es más complicado, ya que la altura h no es independiente del ángulo θ, tal como se aprecia en la figura, sino que h=H+b·sinθ, siendo H la altura del hombro y b la longitud del brazo. (Véase De Luca 2005)

Actividades

Se introduce

La altura h desde la que se dispara el proyectil, actuando en la barra de desplazamiento titulada Altura.
El ángulo de tiro θ, actuando en la barra de desplazamiento titulada Ángulo, o bien, introduciendo el valor del ángulo en el control de edición correspondiente.
La velocidad de disparo se ha fijado en el valor v₀=60 m/s

Se pulsa el botón titulado Empieza

Observamos la trayectoria del proyectil hasta que llega al suelo. En la parte superior del applet, se proporcionan los datos del proyectil:

tiempo t,
las componentes de la velocidad v_x y v_y,
la posición x, e y

Cuando llega al suelo, podemos anotar el alcance x, el tiempo de vuelo t y la velocidad final del proyectil v_x y v_y, y comprobar estos resultados con los cálculos realizados manualmente.

El programa interactivo representa, la trayectoria actual del proyectil y su trayectoria anterior. Fijada la altura h, vamos cambiando el ángulo de tiro θ. Mediante el procedimiento de aproximaciones sucesivas, podemos obtener el ángulo para el cual el alcance es máximo.

CinemaApplet2 aparecerá en un explorador compatible con JDK 1.1.