• Inicio
• Cinemática
• Curvilíneo

Se lanza un objeto desde un péndulo simple

Consideremos un objeto que denominaremos proyectil de masa m que cuelga de una cuerda de longitud l. Cuando se separa de su posición de equilibrio y se suelta comienza a oscilar, tal como estudiaremos en la página dedicada al péndulo simple.

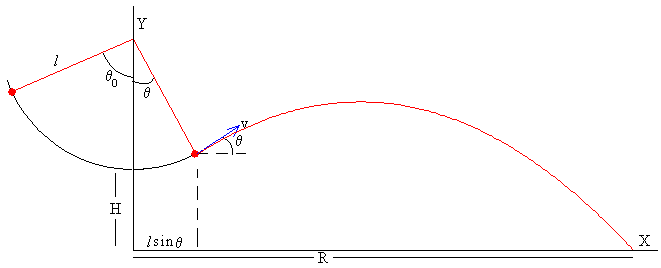
Soltamos el proyectil cuando la cuerda se desvía de la posición de equilibrio un ángulo θ₀. Se corta la cuerda cuando el péndulo se desvía de la posición vertical un ángulo θ<|θ₀|. El proyectil describe una trayectoria parabólica si se desprecia el rozamiento con el aire, tal como se aprecia en la figura.

Principio de conservación de la energía

El proyectil parte de la posición inicial θ₀, con velocidad inicial v=0. Describe un arco de circunferencia y llega a la posición final θ, con velocidad v.  Aplicamos el principio de conservación de la energía para calcular la velocidad v. Si ponemos el nivel cero de energía potencial en la parte más baja de la trayectoria

${\displaystyle \begin{array}{l}mg(l-l\cos {\theta }_0)=\frac{1}{2}m{v}^2+mg(l-l\cos \theta )\\ v=\sqrt{2gl(\cos \theta -\cos {\theta }_0)}\end{array}}$

Ecuaciones del tiro parabólico

Para describir el movimiento del proyectil, situamos los ejes X e Y del modo en el que se señala en la figura; el eje X en el suelo, y el eje Y tiene la dirección del péndulo en la posición de equilibrio θ=0.

El proyectil se dispara con una velocidad v, haciendo un ángulo θ con la horizontal, desde una altura h=H+(l-lcosθ). Siendo H+l la altura del centro de giro del péndulo.

La posición del proyectil en función del tiempo es

x= l·sinθ+v·cosθ·t
y= h+v·sinθ·t-g·t²/2

Siguiendo los mismos pasos que en la sección anterior. Obtenemos el alcance R, poniendo y=0, en la segunda ecuación, despejando el tiempo de vuelo t, y sustituyéndolo en la primera ecuación de la  trayectoria.

${\displaystyle R=\frac{v^2}{g}\left(\text{sin}\theta +\sqrt{{\text{sin}}^2\theta +2z}\right)\cos \theta +l·\text{sin}\theta z=\frac{gh}{v^2}}$

Expresamos el alcance R en función del ángulo θ

${\displaystyle R=2l(\cos \theta -\cos {\theta }_0)\cos \theta \left(\text{sin}\theta +\sqrt{{\text{sin}}^2\theta +\frac{H+l(1-\cos \theta )}{l(\cos \theta -\cos {\theta }_0)}}\right)+l·\text{sin}\theta }$

Dado el ángulo θ₀ de partida del objeto, se tratará de calcular el ángulo θ, para el cual el alcance R es máximo.

Alcance máximo

Dado el ángulo θ₀ de partida del objeto, calcularemos el ángulo θ_m, para el cual el alcance R es máximo.

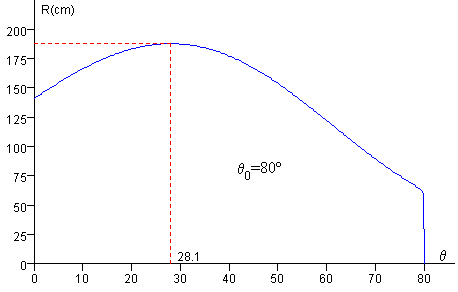
En la figura, se representa el alcance R en función del ángulo θ, para θ₀=80º. El ángulo θ_m para el cual R es máximo se obtiene derivando R respecto del ángulo θ, e igualando a cero. Es decir,  resolviendo la ecuación dR/dθ=0.

En el segundo artículo citado en las referencias, el alcance máximo se obtiene calculando las raíces reales de la ecuación cúbica.

${\displaystyle x^3+\frac{H+l(1-2\cos {\theta }_0)}{l}{x}^2-\frac{H+l(1-\cos {\theta }_0)}{l}=0}$

con x=cosθ_m

Ejemplo:

• Longitud del péndulo l=0.6 m

• Altura del proyectil en la situación de equilibrio, H=1.0 m

• Se desvía el péndulo θ₀=80º de la posición de equilibrio

• Se corta la cuerda cuando el péndulo se desvía θ=30º

La velocidad del proyectil cuando se corta la cuerda es

${\displaystyle v=\sqrt{2·9.8·0.6(\cos 30º-\cos 80º)}=2.85\text{m/s}}$

Ecuaciones del movimiento

x= 0.6·sin30+2.85·cos30·t
y= 1.0+0.6-0.6·cos30+2.85·sin30·t-9.8·t²/2

El alcance se calcula poniendo y=0. Resolvemos la ecuación de segundo grado en t. La raíz positiva vale t=0.64 s

Calculamos el alcance en la primera ecuación x=1.87 m

También podemos calcular el alcance de forma directa

${\displaystyle R=2·0.6(\cos 30-\cos 80)\cos 30\left(\text{sin30}+\sqrt{{\text{sin}}^{2}30+\frac{1.0+0.6(1-\cos 30)}{0.6(\cos 30-\cos 80)}}\right)+0.6·\text{sin}30=1.87\text{m}}$

Para calcular el ángulo θ_m para el cual el alcance es máximo, se resuelve la ecuación cúbica

x³+a·x²+bx+c=0

con a=2.32, b=0, c=-2.49

Se calcula

${\displaystyle Q=\frac{a^2-3b}{9}=\text{0}\text{.60}R=\frac{2a^3-9ab+27c}{54}=-0.78}$

Como R²>Q³ entonces la ecuación tiene una raíz real

${\displaystyle \begin{array}{l}A=-\mathrm{sgn}(R){\left[\left|R\right|+\sqrt{R^2-Q^3}\right]}^{1/3}=1.12\\ x_1=A+\frac{Q}{A}-\frac{a}{3}=0.882\end{array}}$

El ángulo x₁=cosθ_m, θ_m=28.1º

Este ángulo θ_m se puede obtener aproximadamente de forma gráfica.

Actividades

Se introduce

• El ángulo θ₀ que se desvía el péndulo de la posición de equilibrio, actuando en la barra de desplazamiento titulada Angulo partida.

• La longitud del péndulo se ha fijado en l=0.6 m

• La altura del proyectil en la posición de equilibrio θ=0 se ha fijado en H=1.0 m

Se pulsa el botón titulado Nuevo

• El ángulo θ que forma el péndulo con la vertical cuando se corta la cuerda que sostiene el proyectil, actuando en la barra de desplazamiento titulada Angulo final.

Se pulsa el botón titulado Empieza

Cuando el proyectil llega al suelo, se guardan los pares de datos, (ángulo θ, alcance R) en el área de texto situado en la parte izquierda del applet.

Pulsando el botón titulado Gráfica se representa los resultados “experimentales” como puntos de color rojo sobre la representación gráfica de la función R(θ). El alcance R en función del ángulo final θ. Calcula el ángulo θ_m que hace que el alcance R sea máximo

CinemaApplet2 aparecerá en un explorador compatible con JDK 1.1.

Referencias

Buckmaster H. A., Ideal ballistic trajectories revisited. Am. J. Phys. 53 (7) July 1985, pp. 638-641.

Bittel D. Maximizing the range of a projectile launched by a simple pendulum. The Physics Teacher, 43, February 2005, pp. 98-100.

De Luca R. Shot-put kinematics. Eur. J. Phys. 26 (2005), pp. 1031-1036

Curso Interactivo de Física en Internet © Ángel Franco García