• Inicio
• Cinemática
• Curvilíneo

Longitud de la trayectoria

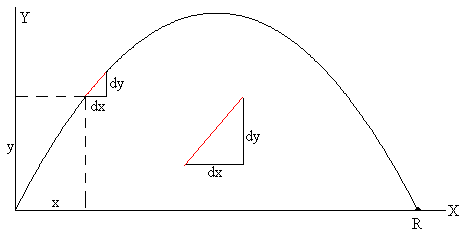
La longitud del elemento diferencial de la trayectoria (en color rojo en la figura) es la hipotenusa de un triángulo rectángulo cuyos catetos tienen longitudes dx y dy,  respectivamente.

${\displaystyle \sqrt{d{x}^2+d{y}^2}={\sqrt{1+\left(\frac{dy}{dx}\right)}}^{2}dx}$

La longitud total del camino recorrido por el proyectil es

${\displaystyle L(\theta )={\displaystyle \underset{0}{\overset{R}{\int }}\sqrt{d{x}^2+d{y}^2}={\displaystyle \underset{0}{\overset{R}{\int }}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}=}{\displaystyle \underset{0}{\overset{R}{\int }}\sqrt{1+{\left(-\frac{g}{v_0^2{\cos }^2\theta }x+\tan \theta \right)}^2}dx}}$

Esta integral es de la forma

${\displaystyle {\displaystyle \int \sqrt{1+u^2}}du=\frac{u}{2}\sqrt{u^2+1}+\frac{1}{2}\ln \left|u+\sqrt{u^2+1}\right|}$

su solución se puede consultar en cualquier libro de Cálculo Diferencial e Integral.

${\displaystyle L(\theta )=-\frac{v_0^2{\cos }^2\theta }{g}{\displaystyle \underset{u_0}{\overset{u_1}{\int }}\sqrt{1+u^2}du}u=\frac{-g}{v_0^2{\cos }^2\theta }x+\tan \theta }$

Al cambiar la variable de x a u cambian los límites de la integral.

• El límite inferior se obtiene para x=0, es decir, para u₀=tanθ

• El límite superior se obtiene para x=R, es decir, para u₁=-tanθ

${\displaystyle L(\theta )=-\frac{v_0^2{\cos }^2\theta }{g}{\displaystyle \underset{u_0}{\overset{u_1}{\int }}\sqrt{1+u^2}du}=-\frac{v_0^2{\cos }^2\theta }{g}\left\{\begin{array}{l}\left(\frac{-\tan \theta }{2}\sqrt{1+{\tan }^2\theta }+\frac{1}{2}\ln \left|-\tan \theta +\sqrt{1+{\tan }^2\theta }\right|\right)\\ -\left(\frac{\tan \theta }{2}\sqrt{1+{\tan }^2\theta }+\frac{1}{2}\ln \left|\tan \theta +\sqrt{1+{\tan }^2\theta }\right|\right)\end{array}\right\}}$

Teniendo en cuenta que 1+tan²θ=1/cos²θ

${\displaystyle \begin{array}{l}L(\theta )=-\frac{v_0^2{\cos }^2\theta }{g}\left\{-\frac{\text{sin}\theta }{{\cos }^2\theta }+\frac{1}{2}\ln \left(\frac{1-\text{sin}\theta }{\cos \theta }\right)-\frac{1}{2}\ln \left(\frac{1+\text{sin}\theta }{\cos \theta }\right)\right\}=\\ -\frac{v_0^2{\cos }^2\theta }{g}\left\{-\frac{\text{sin}\theta }{{\cos }^2\theta }+\frac{1}{2}\ln \left(\frac{1-\text{sin}\theta }{1+\text{sin}\theta }\right)\right\}=-\frac{v_0^2{\cos }^2\theta }{g}\left\{-\frac{\text{sin}\theta }{{\cos }^2\theta }+\frac{1}{2}\ln \left(\frac{1-{\text{sin}}^{\text{2}}\theta }{{(1+\text{sin}\theta )}^2}\right)\right\}=\\ -\frac{v_0^2{\cos }^2\theta }{g}\left\{-\frac{\text{sin}\theta }{{\cos }^2\theta }-\ln \left(\frac{1+\text{sin}\theta }{\cos \theta }\right)\right\}=\frac{v_0^2}{g}\left\{\text{sin}\theta +{\cos }^2\theta \ln \left(\frac{1+\text{sin}\theta }{\cos \theta }\right)\right\}\end{array}}$

En la figura, se muestra que el comportamiento de la longitud L del camino recorrido por el proyectil con el ángulo de tiro θ. La longitud aumenta con el ángulo de tiro θ, alcanzando un máximo y luego vuelve a disminuir.

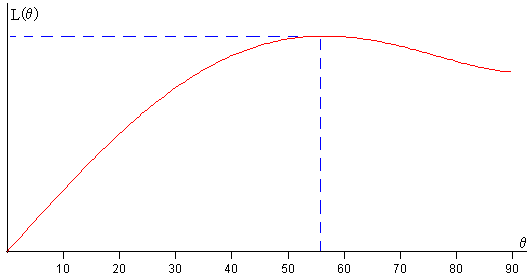
Derivamos L(θ) para hallar el ángulo θ para el cual la longitud de la trayectoria es máxima

${\displaystyle \frac{dL}{d\theta }=2\frac{v_0^2}{g}\cos \theta \left(1-\text{sin}\theta \ln \left(\frac{1+\text{sin}\theta }{\cos \theta }\right)\right)=0}$

Tenemos que resolver la ecuación trascendente

${\displaystyle 1-\text{sin}\theta \ln \left(\frac{1+\text{sin}\theta }{\cos \theta }\right)=0}$

La representación gráfica nos indica que el máximo de L(θ) se encuentra entre 50 y 60º. Se calcula la raíz de la ecuación trascendente por el procedimiento del punto medio. El valor que se obtiene es θ_m=56.46º

Curso Interactivo de Física en Internet © Ángel Franco García