Otros máximos en el tiro parabólico

En esta página, vamos a estudiar otras propiedades de la trayectoria parabólica que describe un proyectil disparado desde el origen con velocidad v₀ haciendo un ángulo θ con la horizontal.

La longitud de la trayectoria
El área que encierra la trayectoria y el eje horizontal
La distancia entre le origen y la posición del proyectil en el instante t.

Ecuación de la trayectoria

Se dispara un proyectil con velocidad v₀ haciendo un ángulo θ con la horizontal. Las ecuaciones del movimiento son

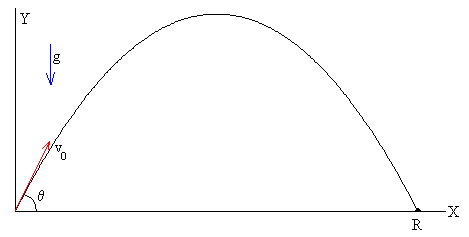
${\begin{cases} a_{x} = 0 \\ a_{y} = - g \end{cases} {\begin{cases} v_{x} = v_{0} \cos θ \\ v_{y} = v_{0} sin θ - g t \end{cases} {\begin{cases} x = v_{0} \cos θ t \\ y = v_{0} sin θ t - \frac{1}{2} g t^{2} \end{cases}$

Eliminando el tiempo t obtenemos la ecuación de la trayectoria

$y = x \tan θ - \frac{1}{2} \frac{g}{v_{0}^{2} \cos^{2} θ} x^{2}$

Alcance

La abscisa R del punto de impacto, denominada alcance se obtiene poniendo y=0 en la ecuación de la trayectoria

$R = \frac{2 v_{0}^{2} sin θ \cos θ}{g} = \frac{v_{0}^{2} sin(2 θ)}{g}$

El máximo valor de R se obtiene para θ=45º

Tiempo de vuelo

Poniendo y=0, y despejando t, tenemos dos soluciones t=0, que corresponde al disparo del proyectil y

$T = \frac{2 v_{0} sin θ}{g}$

El valor máximo de T se obtiene para θ=90º. Cuando el proyectil se lanza verticalmente hacia arriba, describiendo una trayectoria rectilínea a lo largo del eje Y.

Área encerrada por la trayectoria y el eje horizontal X

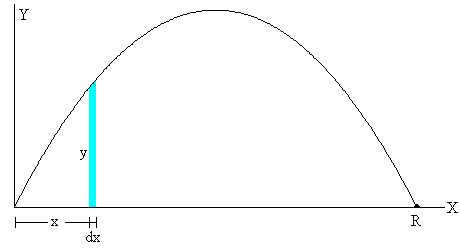
En la figura se muestra el área diferencial y·dx. El área total encerrada entre la trayectoria y el eje X se calcula mediante la integral definida.

$\begin{array}{l} A (θ) = \int_{0}^{R} y \cdot d x = \int_{0}^{R} (x \tan θ - \frac{1}{2} \frac{g}{v_{0}^{2} \cos^{2} θ} x^{2}) d x = {\frac{1}{2} x^{2} \tan θ - \frac{1}{2} \frac{g}{v_{0}^{2} \cos^{2} θ} \frac{x^{3}}{3} |}_{0}^{R} = \\ \frac{1}{2} R^{2} \tan θ - \frac{1}{2} \frac{g}{v_{0}^{2} \cos^{2} θ} \frac{R^{3}}{3} = \frac{2}{3} \frac{v_{0}^{4}}{g^{2}} {sin}^{3} θ \cos θ \end{array}$

En la figura, se muestra que el comportamiento del área total A encerrada entre la trayectoria y el eje X con el ángulo de tiro θ. El área aumenta con el ángulo de tiro θ, alcanzando un máximo y luego vuelve a disminuir, hasta que se hace cero cuando θ=90º

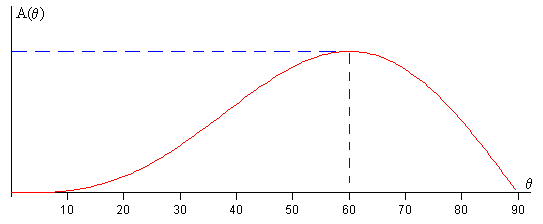
Calculamos el máximo de la función f(θ)=sin³θ·cosθ

$\frac{d f}{d θ} = {sin}^{2} θ (3 \cos^{2} θ - {sin}^{2} θ) = 0 tan θ = \pm \sqrt{3}$

Tiene sentido solamente el signo positivo, que corresponde al ángulo de tiro θ=60º

Cuando se dispara un proyectil con un ángulo de tiro θ=60º, el área encerrada por la trayectoria y el eje horizontal X es máxima.