Otros máximos en el tiro parabólico

Distancia entre el origen del disparo y el proyectil

La distancia d entre el origen O y la posición (x, y) del proyectil en el instante t es

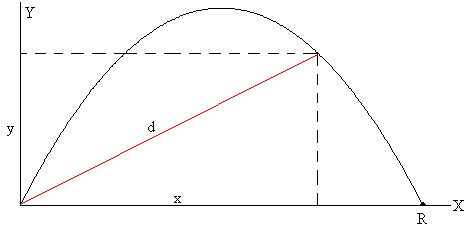
$d^{2} = x^{2} + y^{2} = {(v_{0} \cos θ \cdot t)}^{2} + {(v_{0} sin θ \cdot t - \frac{1}{2} g t^{2})}^{2} = \frac{1}{4} g^{2} t^{4} - v_{0} g sin θ \cdot t^{3} + v_{0}^{2} t^{2}$

El máximo de esta distancia se obtiene igualando la derivada con respecto al tiempo a cero

$g^{2} t^{3} - 3 v_{0} g sin θ \cdot t^{2} + 2 v_{0}^{2} t = 0$

Simplificando entre t, calculamos las raíces de la ecuación de segundo grado en t.

$t_{\pm} = \frac{3 v_{0} sin θ}{2 g} (1 \pm \sqrt{1 - \frac{8}{9 {sin}^{2} θ}})$

Las raíces reales existen cuando el radicando es positivo o nulo

$\frac{8}{9 {sin}^{2} θ} \leq 1 {sin}^{2} θ \geq \frac{8}{9} θ_{0} \geq 70.5 º$

Para ángulos de tiro θ< θ₀ la distancia d entre el origen y el proyectil es una función creciente del tiempo, que alcanza su máximo valor cuando impacta en el suelo.

El máximo d es igual al alcance R y ocurre en el instante T=2v₀sinθ/g que es el tiempo de vuelo.

En el instante t₊ la distancia d₊ entre el origen y la posición del proyectil vale

$\begin{array}{l} d_{+}^{2} = t_{+}^{2} (\frac{1}{4} g^{2} t_{+}^{2} - v_{0} g sin θ \cdot t_{+} + v_{0}^{2}) = \\ {(\frac{3 v_{0} sin θ}{2 g})}^{2} {(1 + \sqrt{1 - \frac{8}{9 {sin}^{2} θ}})}^{2} {\begin{cases} \frac{1}{4} g^{2} {(\frac{3 v_{0} sin θ}{2 g})}^{2} {(1 + \sqrt{1 - \frac{8}{9 {sin}^{2} θ}})}^{2} - \\ v_{0} g sin θ (\frac{3 v_{0} sin θ}{2 g}) (1 + \sqrt{1 - \frac{8}{9 {sin}^{2} θ}}) + v_{0}^{2} \end{cases}} = \\ v_{0}^{2} {(\frac{3 v_{0} sin θ}{2 g})}^{2} {(1 + \sqrt{1 - \frac{8}{9 {sin}^{2} θ}})}^{2} {- \frac{3}{8} {sin}^{2} θ - \frac{3}{8} {sin}^{2} θ \sqrt{1 - \frac{8}{9 {sin}^{2} θ}} + \frac{1}{2}} = \\ \frac{9 v_{0}^{4} {sin}^{2} θ}{4 g^{2}} {2 - \frac{3}{2} {sin}^{2} θ - \frac{4}{9 {sin}^{2} θ} + (\frac{4}{3} - \frac{3}{2} {sin}^{2} θ) \sqrt{1 - \frac{8}{9 {sin}^{2} θ}}} \end{array}$

En el instante t_- la distancia d_- entre el origen y el proyectil vale

$\begin{array}{l} d_{-}^{2} = t_{-}^{2} (\frac{1}{4} g^{2} t_{-}^{2} - v_{0} g sin θ \cdot t_{-} + v_{0}^{2}) = \\ {(\frac{3 v_{0} sin θ}{2 g})}^{2} {(1 - \sqrt{1 - \frac{8}{9 {sin}^{2} θ}})}^{2} {\begin{cases} \frac{1}{4} g^{2} {(\frac{3 v_{0} sin θ}{2 g})}^{2} {(1 - \sqrt{1 - \frac{8}{9 {sin}^{2} θ}})}^{2} - \\ v_{0} g sin θ (\frac{3 v_{0} sin θ}{2 g}) (1 - \sqrt{1 - \frac{8}{9 {sin}^{2} θ}}) + v_{0}^{2} \end{cases}} = \\ v_{0}^{2} {(\frac{3 v_{0} sin θ}{2 g})}^{2} {(1 - \sqrt{1 - \frac{8}{9 {sin}^{2} θ}})}^{2} {- \frac{3}{8} {sin}^{2} θ + \frac{3}{8} {sin}^{2} θ \sqrt{1 - \frac{8}{9 {sin}^{2} θ}} + \frac{1}{2}} = \\ \frac{9 v_{0}^{4} {sin}^{2} θ}{4 g^{2}} {2 - \frac{3}{2} {sin}^{2} θ - \frac{4}{9 {sin}^{2} θ} + (- \frac{4}{3} + \frac{3}{2} {sin}^{2} θ) \sqrt{1 - \frac{8}{9 {sin}^{2} θ}}} \end{array}$

Comprobamos que

$\begin{array}{l} d_{-}^{2} > d_{+}^{2} \\ {2 - \frac{3}{2} {sin}^{2} θ - \frac{4}{9 {sin}^{2} θ} + (- \frac{4}{3} + \frac{3}{2} {sin}^{2} θ) \sqrt{1 - \frac{8}{9 {sin}^{2} θ}}} > \\ {2 - \frac{3}{2} {sin}^{2} θ - \frac{4}{9 {sin}^{2} θ} + (\frac{4}{3} - \frac{3}{2} {sin}^{2} θ) \sqrt{1 - \frac{8}{9 {sin}^{2} θ}}} \\ (- \frac{4}{3} + \frac{3}{2} {sin}^{2} θ) > (\frac{4}{3} - \frac{3}{2} {sin}^{2} θ) \\ {sin}^{2} θ > \frac{8}{9} \end{array}$

De las dos soluciones de la ecuación de segundo grado t₊ y t_- solamente hemos de tener en cuenta la segunda, ya que d_->d₊ para θ>θ₀=70.5º .

Verificamos que el instante t_- es menor que el tiempo de vuelo T

$\frac{t_{-}}{T} = \frac{\frac{3 v_{0} sin θ}{2 g} (1 - \sqrt{1 - \frac{8}{9 {sin}^{2} θ}})}{\frac{2 v_{0}}{g} sin θ} = \frac{3}{4} (1 - \sqrt{1 - \frac{8}{9 {sin}^{2} θ}}) < 1$

Comparamos ahora d- con el alcance R. Vamos a determinar el ángulo θ₁ a partir del cual d_- es mayor que R

$\begin{array}{l} \frac{9 v_{0}^{4} {sin}^{2} θ}{4 g^{2}} {2 - \frac{3}{2} {sin}^{2} θ - \frac{4}{9 {sin}^{2} θ} + (- \frac{4}{3} + \frac{3}{2} {sin}^{2} θ) \sqrt{1 - \frac{8}{9 {sin}^{2} θ}}} > {(\frac{2 v_{0}^{2} sin θ \cos θ}{g})}^{2} \\ \frac{2}{9} + \frac{5}{18} {sin}^{2} θ - \frac{4}{9 {sin}^{2} θ} > (\frac{4}{3} - \frac{3}{2} {sin}^{2} θ) \sqrt{1 - \frac{8}{9 {sin}^{2} θ}} \\ {(\frac{2}{9} + \frac{5}{18} {sin}^{2} θ - \frac{4}{9 {sin}^{2} θ})}^{2} > {(\frac{4}{3} - \frac{3}{2} {sin}^{2} θ)}^{2} (1 - \frac{8}{9 {sin}^{2} θ}) \\ {11sin}^{8} θ - 31 {sin}^{6} θ + 28 {sin}^{4} θ - 7 {sin}^{2} θ - 1 > 0 \end{array}$

La ecuación

11x⁸-31x⁶+28x⁴-7x²-1=0

Tiene dos raíces reales dobles x=1 y x=-1

11x⁸-31x⁶+28x⁴-7x²-1=(x-1)² (x+1)²(11x⁴-9x²-1)

Resolvemos la ecuación bicuadrada

11x⁴-9x²-1=0 haciendo el cambio de variable z=x²

11z²-9z-1=0

La raíces reales son x=±0.95775, que corresponden al ángulo θ=±arcsinx=±73.3º

Para el ángulo θ≥θ₁=73.3º la distancia d_- entre le origen y la posición del proyectil en el instante t_- es mayor que el alcance R

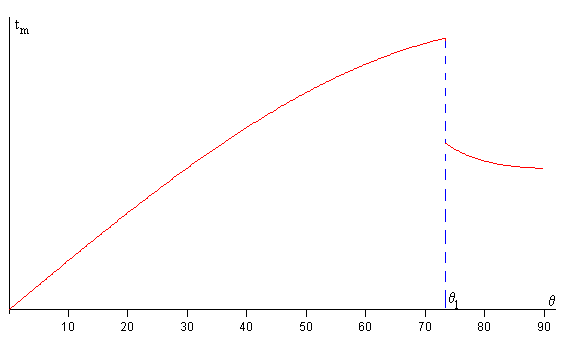
En la figura se muestra, el instante t_m para el cual la distancia d entre el proyectil y el origen es máximo. Para θ<θ₁=73.3º esta distancia es el alcance R y el tiempo t_m=T al tiempo de vuelo. Sorprendentemente, la curva presenta una discontinuidad en θ=θ₁. A partir de este ángulo θ>θ₁, el instante t_m=t_- y la distancia máxima d_m=d_-. Las expresiones de t_- y d_- en función del ángulo de tiro θ las hemos deducido en este apartado.

Ejemplo:

Sea θ=71º>70.5º.

El alcance vale

$R = \frac{v_{0}^{2}}{g} sin(2 \cdot 71) = 0.616 \cdot \frac{v_{0}^{2}}{g}$

El tiempo de vuelo

$T = \frac{v_{0}}{g} 2 \cdot sin 71 = 1.891 \frac{v_{0}}{g}$

El valor máximo de la distancia d_m entre el origen y el proyectil se produce en el instante

$t_{m} = \frac{v_{0}}{g} \frac{3 \cdot sin 71}{2} (1 - \sqrt{1 - \frac{8}{9 \cdot {sin}^{2} 71}}) = 1.311 \frac{v_{0}}{g}$

que es menor que el tiempo de vuelo T

Calculamos la posición del proyectil en el instante t_m

x_m=v₀·cosθ·t_m=0.427·v₀²/g
y_m= v₀·sinθ·t_m-gt_m²/2=0.380·v₀²/g

$d_{m} = \sqrt{x_{m}^{2} + y_{m}^{2}} = 0.572 \frac{v_{0}^{2}}{g}$

que es menor que el alcance R. Luego, para un ángulo de disparo de 71º, la máxima distancia entre el origen y el proyectil se produce en el instante T cuando llega al suelo y es el alcance R.

Sea θ=75º>θ₁=73.3º.

El alcance vale

$R = \frac{v_{0}^{2}}{g} sin(2 \cdot 75) = 0.5 \cdot \frac{v_{0}^{2}}{g}$

El tiempo de vuelo

$T = \frac{v_{0}}{g} 2 \cdot sin 75 = 1.932 \frac{v_{0}}{g}$

El valor máximo de la distancia d_m entre el origen y el proyectil se produce en el instante

$t_{m} = \frac{v_{0}}{g} \frac{3 \cdot sin 75}{2} (1 - \sqrt{1 - \frac{8}{9 \cdot {sin}^{2} 75}}) = 1.134 \frac{v_{0}}{g}$

que es menor que el tiempo de vuelo T

Calculamos la posición del proyectil en este instante

x_m=v₀·cosθ·t_m=0.293·v₀²/g
y_m= v₀·sinθ·t_m-gt_m²/2=0.452·v₀²/g

$d_{m} = \sqrt{x_{m}^{2} + y_{m}^{2}} = 0.539 \frac{v_{0}^{2}}{g}$

que es mayor que el alcance R

Luego, para un ángulo de disparo de 75º, la máxima distancia entre el origen y el proyectil se produce en el instante t_m=1.134v₀/g y vale d_m=0.539·v₀²/g.

Actividades

Se introduce

El ángulo de tiro, actuando en la barra de desplazamiento titulada Ángulo
La velocidad de disparo se ha fijado en v₀=60 m/s

Se pulsa el botón titulado Empieza

Cuando el ángulo de tiro θ>θ₁=73.3º. El programa interactivo calcula el instante t_m para el cual la distancia entre el proyectil y el origen es máxima. Se dibuja el segmento que une ambas posiciones, y se muestra la máxima distancia en la parte superior del applet.

CinemaApplet2 aparecerá en un explorador compatible con JDK 1.1.

Referencias

Sarafian H. On projectile motion. The Physics Teacher. Vol 37, February 1999, pp. 86-88

Hu H, Yu J. Another look at projectile motion. The Physics Teacher Vol 38, October 2000, pp. 423

Mirabelli A. A new projectile problem and the attribution of continuity. Am. J. Phys. 54 (3) March 1986, pp. 278-27