El péndulo esférico visto desde el Sistema de Referencia NO Inercial
Un péndulo esférico es la composición de dos MAS de la misma frecuencia angular ωp pero de direcciones perpendiculares desfasados 90º.
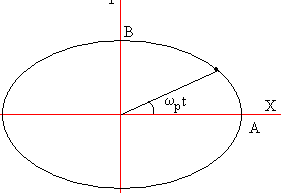 Eliminando el tiempo t en las dos ecuaciones paramétricas, obtenemos la ecuación de la
trayectoria de la partícula en el Sistema de Referencia Inercial, una
elipse de semiejes A y B, tal como se ve en la figura.
Eliminando el tiempo t en las dos ecuaciones paramétricas, obtenemos la ecuación de la
trayectoria de la partícula en el Sistema de Referencia Inercial, una
elipse de semiejes A y B, tal como se ve en la figura.
En un instante t la partícula dista r del origen y hace un ángulo θ con el eje X. La posición de la partícula en el Sistema de Referencia Inercial es
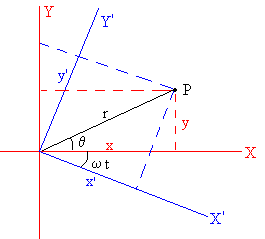
La posición de la partícula el Sistema de Referencia No Inercial es
Las ecuaciones paramétricas del movimiento del péndulo esférico visto desde el Sistema de Referencia No Inercial son:
-
Cuando B=0, el péndulo describe un MAS a lo largo del eje X
Eliminamos el tiempo t de las ecuaciones paramétricas de la trayectoria y obtenemos la ecuación de una circunferencia centrada en el punto (A/2, 0) y de radio A/2.
-
Cuando A=B, el péndulo describe una trayectoria circular
El péndulo describe una trayectoria circular centrada en el origen de frecuencia 2ω
-
Cuando A=B y ωp=-ω, el péndulo describe una trayectoria circular
La trayectoria es el punto fijo (A, 0)
-
Cuando A≠B, el péndulo describe una trayectoria elíptica
Eliminamos el tiempo t de las ecuaciones paramétricas de la trayectoria y obtenemos la ecuación de una circunferencia de radio (A+B)/2 centrada en el punto ((A-B)/2, 0)
Actividades
Se introduce
- La velocidad angular ω de rotación, un número entero, en el control de edición titulado Velocidad angular
- La frecuencia angular ωp del MAS, un número entero, en el control de edición titulado Frecuencia angular
- La relación de las amplitudes B/A de los dos MAS de direcciones perpendiculares, se elige en el control de selección titulado Amplitud (B/A)
Se pulsa el botón titulado Empieza.
Como ejemplo interesante, se sugiere aquel en el que a la frecuencia angular del MAS es igual a la velocidad angular de rotación de la plataforma, ωp=±ω.
Referencias
Daw H. A., Coriolis lecture demostration. Am. J. Phys. 55 (11) November 1987, pp. 1010-101
