Dispersión de partículas alfa por un núcleo

La ley de la Gravitación Universal describe la interacción entre cuerpos debido a su masa. La fuerza de atracción entre dos cuerpos es central y conservativa, su módulo es inversamente proporcional al cuadrado de la distancia que separa los centros de ambos cuerpos. Cuando se integra la ecuación diferencial que describe el movimiento de un cuerpo bajo la acción de dicha fuerza, se obtiene una trayectoria que es una cónica. El tipo de cónica depende signo de la energía total del cuerpo.

Trayectoria	Energía
Elipse	E<0
Parábola	E=0
Hipérbola	E>0

Los planetas describen elipses estando el Sol en uno de sus focos. El hecho de que la energía sea negativa se debe a que la energía potencial de una fuerza atractiva es negativa, y la energía cinética es menor que la energía potencial (el cuerpo está confinado).

La interacción eléctrica puede ser repulsiva o atractiva según que las cargas sean del mismo o distinto signo. La fuerza que describe la interacción eléctrica es central y conservativa, su módulo, de acuerdo a ley de Coulomb, es inversamente proporcional al cuadrado de la distancia que separa ambas cargas.

En este programa, estudiaremos la dispersión de partículas alfa (núcleos de helio) por el núcleo de un átomo, experiencia que condujo a la determinación de la estructura del átomo por el físico Rutherford. En general, la dispersión es de especial interés en física atómica y nuclear. Por ejemplo, cuando un protón, acelerado por un ciclotrón pasa cerca de un núcleo de un átomo del material que constituye el blanco, es desviado o dispersado debido a su repulsión con el núcleo.

En la página anterior, introdujimos el concepto de dispersión con ocasión del estudio del choque de un disco rígido contra un obstáculo puntual . En el modelo estudiado, el obstáculo ejerce una fuerza instantánea que cambia la dirección del disco de acuerdo con la ley de la reflexión. ángulo de dispersión, y la relación cualitativa entre ambas magnitudes.

El objetivo de esta página, es el de profundizar en el estudio del fenómeno de la dispersión, considerando las fuerzas repulsivas de largo alcance que ejerce el núcleo del átomo sobre las partículas alfa incidentes.

Trayectoria de la partícula

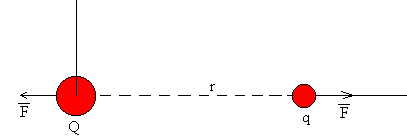
rutherford_1.gif (1741 bytes)

La fuerza de repulsión entre dos cargas Q y q del mismo signo es de acuerdo a la ley de Coulomb

$F = \frac{1}{4 π ε_{0}} \frac{q Q}{r^{2}} \hat{r}$

Esta fuerza es conservativa, y la energía potencial E_p correspondiente es

$E_{p} = \frac{1}{4 π ε_{0}} \frac{q Q}{r}$

Supongamos que Q es una carga fija y que una partícula de masa m y carga q se mueve en el campo creado por la carga Q.

Como la fuerza de repulsión es central y conservativa se cumple

La energía total de la partícula cargada es constante

$E = \frac{1}{2} m v^{2} + \frac{k}{r} k = \frac{q Q}{4 π ε_{0}}$

El momento angular es constante

L=r×mv

Que L sea constante en dirección y sentido quiere decir que la trayectoria de la partícula está contenida en un plano perpendicular a la dirección del momento angular.

Expresamos la energía y el momento angular en coordenadas polares

$\begin{array}{l} E = \frac{1}{2} m {(\frac{d r}{d t})}^{2} + \frac{1}{2} m r^{2} {(\frac{d θ}{d t})}^{2} + \frac{k}{r} \\ L = m r^{2} \frac{d θ}{d t} \end{array}$

Las ecuaciones de constancia del momento angular y de la energía constituyen un par de ecuaciones diferenciales en las que se puede eliminar el tiempo t. Para obtener la ecuación de la trayectoria r=r(θ ) se integra la ecuación diferencial

$\frac{d θ}{d r} = \frac{\frac{L}{m r^{2}}}{\sqrt{\frac{2}{m} (E - \frac{L^{2}}{2 m r^{2}} - \frac{k}{r})}}$

El resultado es una hipérbola

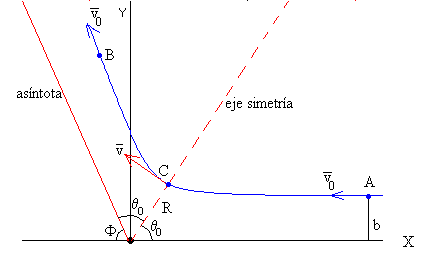
$r = \frac{d}{ε \cos θ - 1} ε = \sqrt{1 + \frac{2 E L^{2}}{m k^{2}}} d = \frac{L^{2}}{m k}$

Las condiciones iniciales son las de una partícula de masa m y carga q que se mueve a gran distancia del centro de fuerzas con velocidad v₀, tal como se muestra en la figura.

Parámetro de impacto

El parámetro de impacto b es la distancia existente entre la dirección de la partícula incidente, cuando se encuentra muy alejada del centro de fuerzas, y el centro de fuerzas. En la figura, el parámetro de impacto b es la distancia entre la dirección de la velocidad v₀, y la carga fija Q.

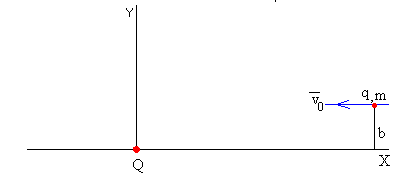
El módulo del momento angular es

L=mv₀·b

Y la energía total

$E = \frac{1}{2} m v_{0}^{2}$

Los valores de d y la excentricidad ε en la ecuación de la hipérbola expresados en términos de la energía E y del parámetro de impacto b son, respectivamente.

$d = \frac{2 E b^{2}}{k} ε = \sqrt{1 + {(\frac{2 E b}{k})}^{2}} k = \frac{q Q}{4 π ε_{0}}$

En la figura, se representa la ecuación de la trayectoria, una hipérbola, que tiene dos asíntotas, dos rectas simétricas con respecto al eje X, que forman un ángulo θ₀ con éste, cuyo valor es

ε ·cosθ₀-1=0 o bien, $\cos θ_{0} = \frac{1}{ε}$

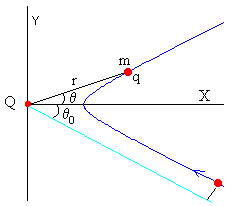
A continuación, giramos la hipérbola en sentido antihorario un ángulo θ₀. La ecuación de la trayectoria en coordenadas polares es

$r = \frac{d}{ε \cos (θ - θ_{0}) - 1}$

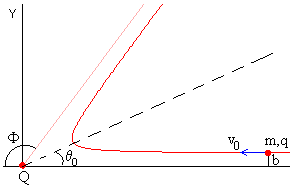
En la figura, se representa la trayectoria de la partícula cargada y en la que se ha señalado, el parámetro de impacto b y el ángulo de dispersión Φ.

Ángulo de dispersión

Cuando la partícula se aleja mucho del centro de fuerzas, sigue una trayectoria que tiende asintóticamente a una línea recta. El ángulo que forma dicha recta con el eje horizontal se denomina ángulo de dispersión.

El ángulo de dispersión vale Φ =180-2θ₀, es decir

$Φ = π - 2 \arccos \frac{1}{\sqrt{1 + {(\frac{2 E b}{k})}^{2}}}$

Ejemplo:

Hemos establecido un sistema de unidades en el que k=1.

El ángulo de dispersión para E=0.5 y b=0.75 vale Φ =106.3º, como podemos comprobar en los programas interactivos.

Actividades

Se introduce

el parámetro de impacto b
la energía de la partícula E, un número positivo, ya que la fuerza es repulsiva.

Se pulsa el botón titulado Empieza

Se representa la trayectoria de la partícula y se calcula el ángulo de dispersión Φ

DispersionApplet aparecerá en un explorador compatible con JDK 1.1.

Ejercicio

Usando el principio de conservación de la energía calcular la distancia mínima de aproximación de una partícula cargada, que choca de frente contra un núcleo atómico

Para hacer más simple el problema supondremos que la masa del núcleo es mucho mayor que la masa del proyectil.

Si la carga del núcleo es Q y la del proyectil es q. La energía total del proyectil es

$E = \frac{1}{2} m v^{2} + \frac{Q q}{4 π ε_{0} r} = \frac{1}{2} m v_{0}^{2}$

Cuando el proyectil está a mucha distancia del núcleo, su velocidad es v₀, y toda la energía es cinética. En el punto C de máximo acercamiento (véase la figura), la velocidad v es transversal (perpendicular a la dirección radial) de modo que el momento angular es L=mRv. La ecuación de la conservación de la energía en dicho punto de máximo acercamiento se escribe

$\frac{L^{2}}{2 m R^{2}} + \frac{Q q}{4 π ε_{0} R} = \frac{1}{2} m v_{0}^{2}$

Ecuación de segundo grado en 1/R que permite obtener R en función de la energía y del momento angular de la partícula.

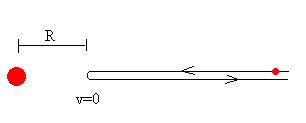
Para una colisión de frente, L=0 y se despeja R

$R = \frac{q Q}{4 π ε_{0} (\frac{1}{2} m v_{0}^{2})}$

En una colisión frontal, la velocidad de la partícula en el punto de máximo acercamiento es cero, v=0

Relación entre parámetro de impacto y ángulo de dispersión

En el apartado anterior, hemos obtenido la relación cuantitativa entre el parámetro de impacto y el ángulo de dispersión para una energía E de la partícula cargada. Mediante el programa interactivo que viene a continuación, se puede establecer una relación cualitativa, observando las trayectorias de un número de partículas de la misma energía que inciden sobre el centro fijo de fuerzas con parámetros de impacto espaciados regularmente.

Se introduce

la energía de la partícula E, un número positivo, actuando en la barra de desplazamiento titulada Energía

Se pulsa el botón titulado Empieza

Se observa las trayectorias de las partículas que inciden sobre el centro fijo de fuerzas

Cuando se han trazado todas las trayectorias, se pulsa el botón titulado Gráfica

Se representa en el eje vertical, el ángulo de dispersión Ф y en el eje horizontal, el parámetro de impacto b.

DispersionApplet aparecerá en un explorador compatible con JDK 1.1.

La envolvente

La ecuación de la trayectoria la podemos escribir de la forma

$\begin{array}{l} \frac{1}{r} = \frac{ε}{d} \cos (θ - θ_{0}) - \frac{1}{d} \\ \frac{1}{r} = \frac{ε}{d} (\cos θ \cdot \cos θ_{0} + \sin θ \cdot \sin θ_{0}) - \frac{1}{d} \\ \frac{1}{r} = \frac{ε}{d} \cos θ_{0} (\cos θ + \sin θ \cdot \tan θ_{0}) - \frac{1}{d} \end{array}$

Teniendo en cuenta las relaciones

$\begin{array}{l} \cos θ_{0} = \frac{1}{ε} ε = \sqrt{1 + {(\frac{2 E b}{k})}^{2}} d = \frac{2 E b^{2}}{k} \\ \cos θ_{0} = \frac{1}{\sqrt{1 + \tan^{2} θ_{0}}} \tan θ_{0} = \frac{2 E b}{k} \end{array}$

La ecuación de la trayectoria se escribe en términos del parámetro b

$\frac{1}{r} = \frac{k}{2 E b^{2}} (\cos θ - 1) + \frac{\sin θ}{b}$

La ecuación de la trayectoria depende del parámetro de impacto b,
f(r, θ, b)=0

La ecuación de la envolvente de las trayectorias se obtiene derivando con respecto a b e igualando a cero.

$\begin{array}{l} \frac{\partial f}{\partial b} = 0 \\ - \frac{k}{E b^{3}} (\cos θ - 1) + \frac{\sin θ}{b^{2}} = 0 \\ b = \frac{(1 - \cos θ)}{\sin θ} \frac{k}{E} \end{array}$

y combinando ésta con la ecuación de la trayectoria para eliminar el parámetro b. Es decir, se introduce la expresión de b en la ecuación de la trayectoria.

$\frac{1}{r} = \frac{E}{2 k} (1 + \cos θ)$

Esta es la ecuación de la envolvente en coordenadas polares. Para escribirla en coordenadas rectangulares, ponemos
x=r·cosθ, y=r·sinθ

$\begin{array}{l} \frac{2 k}{E} = \sqrt{x^{2} + y^{2}} + x \\ y^{2} = \frac{4 k}{E} (\frac{k}{E} - x) \end{array}$

En este último applet, podemos apreciar la envolvente (en color azul) de las trayectorias hiperbólicas que describen las partículas

Referencias

French A. P. The envelopes of some families of fixed-energy trajectories. Am. J. Phys. 61 (9) September 1993