Choque de dos esferas iguales

En esta página, se estudia el choque de dos esferas iguales que cuelgan de sendos hilos inextensibles y de masa despreciable.

Las esferas se separan de su posición de equilibrio, ángulos iguales, se sueltan y se observa cómo decae la amplitud de sus oscilaciones como consecuencia de los choques.

Descripción

Movimiento de las esferas

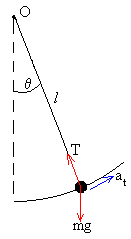La descripción del movimiento de cada una de las esferas es similar al de un péndulo formado por una masa puntual m que cuelga de un hilo inextensible de longitud l.

La ecuación del movimiento es

m·a_t=-mg·sinθ

$\frac{d^{2} θ}{d t^{2}} + \frac{g}{l} \sin θ = 0$

Para determinar la posición angular θ de cada péndulo (el ángulo que forma con la vertical) en función del tiempo, se resuelve la ecuación diferencial por procedimientos numéricos en dos etapas con las siguientes condiciones iniciales:

Movimiento hacia arriba: en la posición θ=0, la velocidad angular dθ/dt=v/l, siendo v la velocidad de la esfera después del choque.
Movimiento hacia abajo: en la posición θ=θ₀ de máximo desplazamiento, la velocidad angular es dθ/dt=0

Balance energético

Comparemos dos posiciones del péndulo:

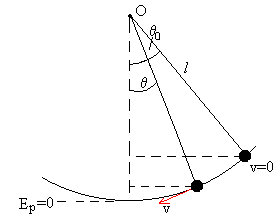En la posición extrema θ=θ₀, la energía es solamente potencial.

E=mg(l-l·cosθ₀)

En la posición θ, la energía del péndulo es parte cinética y la otra parte potencial

$E = \frac{1}{2} m v^{2} + m g (l - l \cos θ)$

La energía se conserva

v²=2gl(cosθ-cosθ₀)

La velocidad u de cada una de las esferas justamente antes del choque, cuando θ=0 es

u²=2gl(1-cosθ₀)

Choque de dos esferas

Las velocidades de las esferas v₁=-v y v₂=v después del choque están relacionadas con las velocidades u₁=u y u₂=-u antes del choque mediante

v₁-v₂=-e(u₁-u₂)
-2v=-e(2u),

La velocidad v de las esferas después del choque disminuye ya que el coeficiente de restitución e<1.

v=e·u

Sucesivos choques de las dos esferas

En la figura, se muestra:

La posición inicial de partida, cuando la velocidad angular inicial es cero.
Las dos esferas justamente antes del choque
Las dos esferas justamente después del choque
La posición final de máximo alejamiento de las esferas, cuando alcanzan la desviación máxima

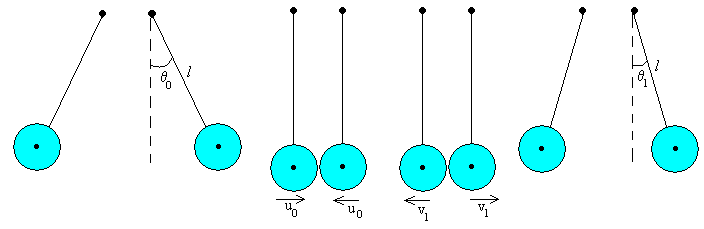
Primer choque

En el instante t=0, las esferas se encuentran desviadas de su posición de equilibrio un ángulo θ₀, y a continuación, se sueltan. Se van acercando hasta que alcanzan la posición angular θ=0, justamente antes del choque. Su velocidad u₀ es

$u_{0}^{2} = 2 g l (1 - \cos θ_{0})$

La velocidad v₁de cada una de las esferas justamente después del choque es

v₁=e·u₀

Las esferas se alejan una de la otra hasta que alcanzan su máxima desviación θ₁

$v_{1}^{2} = 2 g l (1 - \cos θ_{1})$

La relación entre las desviaciones máximas inicial θ₀ y final θ₁ es

$\cos θ_{1} = 1 - e^{2} + e^{2} \cos θ_{0}$

Segundo choque

La velocidad u₁ de cada una de las esferas justamente antes del segundo choque es la misma que la velocidad v₁ de las esferas justamente después del primer choque, por el principio de conservación de la energía.

u₁=v₁

La velocidad v₂ de cada una de las esferas justamente después del choque será

v₂=e·u₁

Las esferas se alejan una de la otra hasta que alcanzan su desviación máxima θ₂

$v_{2}^{2} = 2 g l (1 - \cos θ_{2})$

La relación entre las desviaciones máximas inicial θ₁ y final θ₂ es

$\begin{array}{l} \cos θ_{2} = 1 - e^{2} + e^{2} \cos θ_{1} \\ \cos θ_{2} = 1 - e^{4} + e^{4} \cos θ_{0} \end{array}$

n choque

La relación entre dos ángulos consecutivos θ_n y θ_n-1de desviación máxima es

$\cos θ_{n} = 1 - e^{2} + e^{2} \cos θ_{n - 1}$

La relación entre el el último θ_n y el inicial θ₀ es

$\cos θ_{n} = 1 - e^{2 n} + e^{2 n} \cos θ_{0}$

En vez de medir ángulos, es más cómodo medir la proyección x_n del centro de la esfera sobre el eje horizontal X

x_n=l·sinθ_n

Balance energético

A medida que las esferas chocan su energía va disminuyendo. La energía inicial de cada una de las esferas es

E₀=mg(l-l·cosθ₀)

Después de n choques la energía de cada una de las esferas es

$\begin{array}{l} E_{n} = m g (l - l \cos θ_{n}) = m g l e^{2 n} (1 - \cos θ_{0}) \\ E_{n} = e^{2 n} E_{0} \end{array}$

Ejemplo

Se desvía cada una de las esferas un ángulo de θ₀=90º de la posición de equilibrio

En el siguiente cuadro, se especifica la máxima desviación θ_n, la proyección en dicha posición x_n del centro de la esfera sobre el eje X, y la energía E_n.

e=0.8
θ	x/l	E/E₀
90º	1.00	1.0
69º	0.93	0.64
54º	0.81	0.41
42º	0.67	0.26
34º	0.55	0.17
27º	0.45	0.11

Actividades

Se introduce

El coeficiente de restitución e, actuando en la barra de desplazamiento titulada Coef. restitución.

Se pulsa el botón titulado Empieza

Se observa el movimiento de las dos esferas idénticas que parten de la posición θ₀=90º y a continuación se sueltan.

Las esferas se acercan, chocan, se alejan hasta que alcanzan la desviación máxima y así, sucesivamente.

Sobre el eje horizontal, se van marcando las proyecciones del centro de una de las esferas cuando alcanzan la desviación máxima.

En la parte izquierda del applet, se muestra el balance energético:

La energía cinética, la energía potencial, y la suma de ambas.
La energía total, se representa mediante un segmento horizontal de color negro.

En la parte superior del applet se proporcionan los datos de

El ángulo de desviación de uno de los péndulos en función del tiempo
La velocidad angular en función del tiempo, que nos permitirá medir la desviación máxima cuando se hace cero.
La energía total E dividida por la energía inicial E₀.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.