Movimiento vertical de un cohete (I)

Examinaremos ahora, el movimiento de un cohete que es lanzado verticalmente desde la superficie de la Tierra. Supondremos que se trata de un cohete pequeño, que alcanza una altura limitada. Podemos considerar que la intensidad de la gravedad g es aproximadamente constante e igual a 9.8 m/s².

Analizaremos las dos etapas en el movimiento del cohete:

Desde que se lanza hasta que agota el combustible
Desde el momento en el que agota el combustible, hasta que alcanza la máxima altura.

Descripción

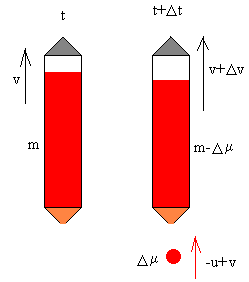Consideremos un cohete que en el instante t, tiene una masa m que lleva una velocidad v respecto a un Sistema de Referencia Inercial (por ejemplo, la Tierra).

En el instante t+Δt, una masa Δμ de combustible se expulsa con una velocidad constante –u relativa al cohete, como consecuencia la velocidad de la masa restante (m-Δμ) del cohete se incrementa en v+Δv.

En el instante t, el cohete de masa m lleva una velocidad v. El momento lineal es

p(t)=mv

En el instante t+Δt

El cohete tiene una masa m-Δμ, su velocidad es v+Δv.
La masa expulsada Δμ lleva una velocidad –u respecto del cohete o una velocidad –u+ v, respecto de Tierra

El momento lineal en este instante es

p(t+Δt)=(m-Δμ)(v+Δv)+ Δμ(–u+ v)

El cambio de momento lineal entre los instantes t y t+Δt es

Δp= p(t+Δt)- p(t)=m·Δv- u·Δμ-Δμ·Δv

En el límite cuando Δt→0

$\frac{d p}{d t} = m \frac{d v}{d t} - u \frac{d μ}{d t}$

El cambio de momento lineal se debe a la acción de las fuerzas exteriores al sistema (la fuerza de atracción gravitatoria, que apunta en sentido contrario al momento lineal).

$\frac{d p}{d t} = - m g$

Por otra parte, la masa M del sistema formado por el cohete m y el combustible expulsado μ es constante M=μ+m, por lo que dμ+dm=0. La masa del cohete disminuye en dm y aumenta la masa del combustible expulsado en la misma cantidad.

La ecuación del movimiento del cohete se escribe

$- m g = m \frac{d v}{d t} + u \frac{d m}{d t}$

Suponemos que la cantidad de combustible quemado en la unidad de tiempo, D, es constante, D=-dm/dt. La masa m del cohete en el instante t valdrá m=m₀-D·t. Donde m₀ es la suma de la carga útil más el combustible inicial, y D·t es el combustible quemado al cabo de un cierto tiempo t.

$m \frac{d v}{d t} = u D - m g$

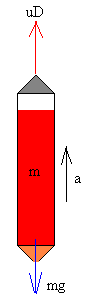
Un cohete puede considerarse una partícula de masa variable m sometida a dos fuerzas de la misma dirección pero de sentidos contrarios: el empuje de los gases uD y el peso mg.

Como caso particular, mencionaremos que en el espacio exterior el peso mg vale cero, y sobre el cohete actuaría únicamente la fuerza de empuje que le proporciona la expulsión de los gases al quemarse el combustible.

La ecuación anterior la podemos escribir

$\frac{d v}{d t} = - g + u \frac{D}{m_{0} - D t}$

Que se puede integrar de forma inmediata

$\int_{v_{0}}^{v} d v = \int_{0}^{t} (- g + u \frac{D}{m_{0} - D t}) d t$

obteniéndose la expresión de la velocidad en función del tiempo

$v = v_{0} - g t + u \cdot \ln \frac{m_{0}}{m_{0} - D t}$

Volviendo a integrar

$x - x_{0} = \int_{0}^{t} v \cdot d t$

Se obtiene la posición x del móvil en cualquier instante t.

$x = x_{0} + v_{0} t - \frac{1}{2} g t^{2} + u t \ln m_{0} + \frac{u}{D} [(m_{0} - D t) \ln (m_{0} - D t) + D t - m_{0} \ln m_{0}]$

Ejemplos

El empuje es mayor que peso

Combustible total en el cohete, 1.0 kg
Carga útil que transporta, 2.0 kg
Combustible quemado por segundo, D=0.1 kg/s
Velocidad de salida de los gases u₀=1000 m/s

Se considera despreciable la masa del recipiente que contiene el combustible

Fuerzas sobre el cohete

Masa total del cohete=carga útil+combustible

m₀=2.0+1.0=3.0 kg

El peso del cohete m₀·g (29.4 N) es menor que el empuje u·D (100 N)

Tiempo que tarda en agotarse el combustible

Como hay 1.0 kg de combustible que se queman a razón de 0.1 kg/s. Luego, el combustible se agota en el instante t₀= 10 s.

Velocidad máxima alcanzada por el cohete

$\begin{array}{l} v = - 9.8 \cdot t + u \ln \frac{m_{0}}{m_{0} - D t} \\ v = - 9.8 \cdot 10 + 1000 \ln (\frac{3}{3 - 1}) = 307 m/s \end{array}$

Altura que alcanza hasta que se agota el combustible

$\begin{array}{l} x = - \frac{1}{2} g t^{2} + u t \ln m_{0} + \frac{u}{D} [(m_{0} - D t) \ln (m_{0} - D t) + D t - m_{0} \ln m_{0}] \\ x = - 4.9 \cdot 10^{2} + 1000 \cdot 10 \cdot \ln 3 + \frac{1000}{0.1} [2 \ln 2 + 1 - 3 \ln 3] = 1400 m \end{array}$

Una vez que ha agotado el combustible, el cohete prosigue su movimiento hasta que alcanza la máxima altura. Las ecuaciones del movimiento son

$\begin{array}{l} v = v_{0} - g (t - t_{0}) \\ x = x_{0} + v_{0} (t - t_{0}) - \frac{1}{2} g {(t - t_{0})}^{2} \end{array}$

Donde x₀, v₀ es la posición, velocidad del cohete en el instante t₀ en el que se ha agotado el combustible.

La altura máxima se alcanza cuando v=0, en el instante t=41.4 s. La posición del cohete en dicho instante es x=6223 m.

El empuje es menor que peso

Combustible total en el cohete, 2.0 kg
Carga útil que transporta, 9.0 kg
Combustible quemado por segundo, D=0.1 kg/s
Velocidad de salida de los gases u₀=1000 m/s

Se considera despreciable la masa del recipiente que contiene el combustible

Fuerzas sobre el cohete

El peso del cohete (2.0+9.0)·9.8=107.8 N es mayor que el empuje u·D=1000·0.1=100 N

Se va quemando el combustible sin que se mueva el cohete hasta el momento en el que el peso se iguala al empuje.

(c+9)·9.8=100

Cuando el combustible c=1.204 kg el cohete empieza a elevarse. Se han desperdiciado 2-1.204=0.796 kg de combustible.

Masa inicial del cohete al despegue

m₀=1.204+9.0=10.204 kg

Tiempo que tarda en agotarse el combustible

Como hay 1.204 kg de combustible que se queman a razón de 0.1 kg/s. Luego, el combustible se agota en 12.04 s.

Velocidad máxima alcanzada por el cohete

$\begin{array}{l} v = - 9.8 \cdot t + u \ln \frac{m_{0}}{m_{0} - D t} \\ v = - 9.8 \cdot 12.04 + 1000 \ln (\frac{10.204}{9}) = 7.56 m/s \end{array}$

Altura que alcanza hasta que se agota el combustible

$\begin{array}{l} x = - \frac{1}{2} g t^{2} + u t \ln m_{0} + \frac{u}{D} [(m_{0} - D t) \ln (m_{0} - D t) + D t - m_{0} \ln m_{0}] \\ x = - 4.9 \cdot {12.04}^{2} + 1000 \cdot 10.204 \cdot \ln 10.204 + \frac{1000}{0.1} [9 \ln 9 + 0.1 \cdot 12.04 - 10.204 \ln 10.204] = 29.62 m \end{array}$

Tiempo que tarda en alcanzar la máxima altura

0=7.56-9.8(t-12.04)
t=12.8 s

Posición del cohete en dicho instante

x=29.62+7.56·0.77-4.9·0.77²=32.5 m

Actividades

Se introduce:

Combustible total en el cohete, en el control de edición titulado Combustible total en el cohete
Carga útil que transporta, en el control de edición titulado Carga útil que transporta
Combustible quemado por segundo, en el control de edición titulado Combustible quemado por seg.
Velocidad de salida de los gases u₀=1000 m/s

Se pulsa el botón titulado Empieza

Al lado del cohete, dos flechas, se dibujan las fuerzas sobre el cohete: en color rojo el empuje y en color azul el peso. El empuje permanece constante, el peso va disminuyendo a medida que se va quemando el combustible.

Si el peso inicial del cohete (carga útil más combustible) m₀·g es mayor que el empuje proporcionado por la expulsión de los gases u·D, el cohete quema el combustible sin despegar, hasta el momento en el que el peso se hace igual o menor que el empuje.

Una vez que despega, el cohete agota el combustible en el instante t, cociente entre la masa combustible y el combustible quemado por segundo.

La velocidad que alcanza el cohete cuando agota el combustible se obtiene mediante la fórmula

$v = - 9.8 \cdot t + u \ln \frac{m_{0}}{m_{0} - D t}$

donde m₀ es la masa del cohete al despegar, y t es el tiempo desde que despega hasta que agota el combustible. Después, el cohete continúa ascendiendo hasta que su velocidad se hace cero.

En la parte derecha del applet, se representa la velocidad del cohete en función del tiempo.
En la parte izquierda del applet, observamos la altura del cohete en función del tiempo.