Movimiento de una esfera en un fluido viscoso. Fórmula de Stokes

En esta página, se describe el movimiento vertical de una esfera de masa m y de radio R, en el seno de un fluido viscoso, en régimen laminar.

Descripción

La esfera se mueve bajo la acción de las siguientes fuerzas: el peso, el empuje (se supone que el cuerpo está completamente sumergido en el seno de un fluido), y una fuerza de rozamiento que es proporcional a la velocidad de la esfera (suponemos que el flujo se mantiene en régimen laminar).

El peso es el producto de la masa por la aceleración de la gravedad g. La masa es el producto de la densidad del material ρ_e por el volumen de la esfera de radio R.

$m g = ρ_{e} \frac{4}{3} π R^{3} g$

De acuerdo con el principio de Arquímedes, el empuje es igual al producto de la densidad del fluido ρ_f, por el volumen del cuerpo sumergido, y por la aceleración de la gravedad.

$E = ρ_{f} \frac{4}{3} π R^{3} g$

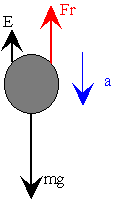Din_3.gif (1985 bytes) La fuerza de rozamiento es proporcional a la velocidad, y su expresión se denomina ley de Stokes

F_r=6πRηv

donde η es la viscosidad del fluido.

La ecuación del movimiento será, por tanto,

ma=mg-E-F_r

La velocidad límite, se alcanza cuando la aceleración sea cero, es decir, cuando la resultante de las fuerzas que actúan sobre la esfera es cero.

mg-E=F_r

Despejamos la velocidad límite v_l

$v_{l} = \frac{2 g (ρ_{e} - ρ_{f}) R^{2}}{9 η}$

La ecuación del movimiento es

$m \frac{d v}{d t} = F - k v$

donde F es la diferencia entre el peso y el empuje F=mg-E, y k=6πRη

Integramos la ecuación del movimiento para obtener la velocidad de la esfera en función del tiempo.

$\int_{0}^{v} \frac{d v}{\frac{F}{m} - \frac{k}{m} v} = \int_{0}^{t} d t$

Obtenemos

$v = v_{l} (1 - \exp (\frac{- k t}{m})) v_{l} = \frac{F}{k}$

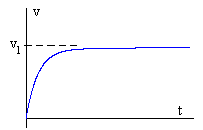Esta ecuación nos dice que se alcanza la velocidad límite v_l después de un tiempo teóricamente infinito. Si representamos v en función del tiempo t la gráfica tienen una asíntota horizontal en v=v_l.

Integramos la expresión de la velocidad en función del tiempo para obtener la posición x del móvil en función del tiempo t. Suponemos que la esfera parte del origen x=0, en el instante inicial t=0.

$x = \int_{0}^{t} v d t x = v_{l} (t - \frac{m}{k} (1 - \exp (\frac{- k t}{m})))$

Dado que la exponencial tiende a cero rápidamente a medida que transcurre el tiempo, vemos que al cabo de un cierto tiempo, el desplazamiento x del móvil será proporcional al tiempo t.

Las diferencias entre el movimiento de un cuerpo en caída libre y cuando cae en el seno de un fluido viscoso se pueden resumir en el siguiente cuadro

Caída libre	En el seno de un fluido viscoso
La velocidad es proporcional al tiempo	La velocidad tiende hacia un valor constante
El desplazamiento es proporcional al cuadrado del tiempo.	El desplazamiento es proporcional al tiempo.

Actividades

Se elige el material de la esfera, en el control de selección titulado Esfera
El radio en mm de la esfera
Se elige el fluido, en el control de selección titulado Fluido

Se pulsa el botón titulado Empieza

Se pueden introducir en los controles de edición, otros valores distintos de los que figuran en las tablas

Material de la esfera	Densidad (g/cm³)
Hierro	7.88
Aluminio	2.70
Cobre	8.93
Plomo	11.35
Volframio	19.34

Fluido	Densidad (g/cm³)	Viscosidad (kg/m·s)
Agua	1.0	0.00105
Glicerina	1.26	1.3923
Benceno	0.88	0.000673
Aceite	0.88	0.391

Fuente: Koshkin N. I., Shirkévich M. G.. Manual de Física Elemental. Editorial Mir 1975.

Para determinar la dependencia de la velocidad límite con el radio de la esfera, con la densidad del material, con la densidad y viscosidad del fluido:

Elegir esferas de distinto radio, del mismo material y que se muevan en el mismo fluido.
Elegir esferas del mismo radio pero de distinto material, y que se muevan en el mismo fluido.
Cambiar el fluido en el que se mueven las esferas, manteniendo sus dimensiones y su material constitutivo.

El círculo de color rojo representa la esfera que cae en el seno de un fluido viscoso. Al lado se representa las fuerzas sobre la esfera.

En color rojo, la fuerza F constante que es la diferencia entre el peso y el empuje del fluido.
En color azul, la fuerza de rozamiento proporcional a la velocidad kv.

Cuando ambas flechas son aproximadamente iguales, la velocidad de la esfera es constante e igual a la velocidad límite.

Ejemplo:

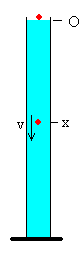En un tubo vertical lleno de aceite de automóvil dejamos caer perdigones de plomo. El diámetro del tubo es mucho mayor que el diámetro del perdigón. Los datos son

Densidad del plomo ρ_e=11.35 g/cm³
Radio de la esfera R=1.96 mm
Densidad del aceite ρ_f=0.88 g/cm³
Viscosidad del aceite η=0.391 kg/(m·s)

Se alcanza el 99.5% de la velocidad límite constante en el instante t tal que

$\frac{v}{v_{l}} = 0.995 = 1 - \exp (\frac{- k t}{m})$

Donde k=6πRη=0.014 kg/s, y la masa de la esfera es m=ρ_e4/3πR³=3.58·10^-4 kg

Despejamos el tiempo t=0.13 s

La esfera se habrá desplazado en este tiempo x=0.023 m

Si dejamos caer la bolita desde la superficie del aceite, podemos comenzar a tomar medidas con seguridad 3 centímetros por debajo de dicha superficie.

En este ejemplo, se ha supuesto que el fluido se mantiene en régimen laminar cuando se mueve la esfera en su seno. Veremos más adelante, que la fórmula de Stokes tiene un rango de validez que se expresa en términos del denominado número de Reynolds.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.