• Inicio
• Dinámica
• Movimiento en un fluido viscoso

Fuerza de rozamiento proporcional al cuadrado de la velocidad.

Si despreciamos el empuje, las fuerzas que actúan sobre el cuerpo de masa m son:

• El peso mg
• La fuerza de rozamiento F_r, que es de sentido contrario al vector velocidad (tangente a la trayectoria). F_r=-bmv·v.

Las ecuaciones del movimiento del cuerpo serán por tanto.

${\displaystyle \begin{array}{l}m\frac{d{v}_x}{dt}=-mb{v}_x\sqrt{v_x^2+v_y^2}\\ m\frac{d{v}_y}{dt}=-mg-mb{v}_y\sqrt{v_x^2+v_y^2}\end{array}}$

Este sistema de ecuaciones diferenciales acopladas se resuelven aplicando procedimientos numéricos, por ejemplo, el método de Runge-Kutta.

Las condiciones iniciales son las misma que en la sección anterior t=0, v_0x=v₀·cosθ , v_0y=v₀·sinθ , x=0, y=0

Actividades

En el applet introducimos:

• El valor del parámetro b en unidades m^-1, en el control de edición titulado b
• La velocidad inicial v₀ en el control de edición titulado Velocidad inicial.

Se pulsa el botón titulado Empieza

El programa interactivo traza y calcula el alcance de los proyectiles disparados con ángulos de 10, 15, 20, 25, 30, 35, 40 y 45º (en color rojo).

Compara estas trayectorias con la que seguiría el mismo proyectil disparado con un ángulo de 45º en el vacío (en color azul).

En la parte superior derecha del applet, se muestra el alcance (aproximado) de cada uno de los proyectiles. Podemos observar que el máximo alcance del proyectil no se obtiene para el ángulo de disparo de 45º sino para un ángulo inferior. Y como cabía esperar, el alcance del proyectil disparado con 45º es inferior en un medio como el aire que en el vacío.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Alcance, altura máxima y tiempo de vuelo

En el apartado anterior, se ha calculado la trayectoria del proyectil resolviendo un sistema de dos ecuaciones diferenciales de segundo orden. En este apartado, vamos a integrar las ecuaciones del movimiento para calcular el alcance, el tiempo de vuelo y la altura máxima.

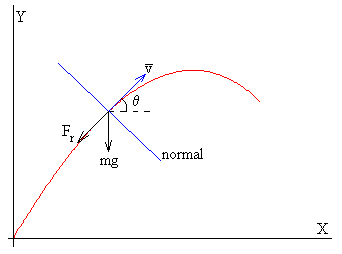Cambiamos de sistema de referencia, y escribimos las ecuaciones del movimiento en la dirección tangencial y en la dirección normal

${\displaystyle \begin{array}{l}m\frac{dv}{dt}=-mb{v}^2-mg\sin \theta \\ m\frac{v^2}{\rho }=mg\cos \theta \end{array}}$

donde ρ es el radio de curvatura de la trayectoria.

En el intervalo de tiempo comprendido entre t y t+dt, la dirección del vector velocidad cambia un ángulo dθ, que es el ángulo entre las tangentes o entre las normales. El móvil se desplaza en este intervalo de tiempo un arco ds=ρ·dθ,  tal como se aprecia en la figura.

 

 

${\displaystyle \frac{dv}{dt}=\frac{dv}{ds}\frac{ds}{dt}=v\frac{dv}{ds}=\frac{v}{\rho }\frac{dv}{d\theta }}$

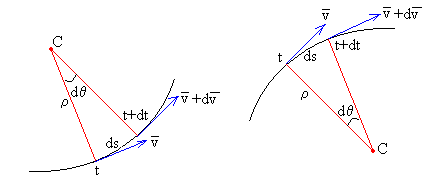
Hemos de tener en cuenta que la curvatura de la trayectoria es negativa (figura de la derecha). La curva queda a la derecha de la tangente tomada en sentido de las x crecientes. La igualdad anterior se escribe para este caso

${\displaystyle \frac{dv}{dt}=-\frac{v}{\rho }\frac{dv}{d\theta }}$

Las ecuaciones del movimiento en la dirección tangencial y en la dirección normal se convierten en una única ecuación diferencial de primer orden.

${\displaystyle \begin{array}{l}\frac{g\cos \theta }{v}\frac{dv}{d\theta }=b{v}^2+g\sin \theta \\ \frac{1}{v^3}\frac{dv}{d\theta }-\frac{1}{v^2}\tan \theta =\frac{b}{g\cos \theta }\end{array}}$

Haciendo el cambo de variable u=1/v²

${\displaystyle \frac{du}{d\theta }+2\tan \theta ·u=\frac{-2b}{g\cos \theta }}$

Esta ecuación es del tipo lineal (véase Puig Adam P., Curso teórico-práctico de Ecuaciones Diferenciales aplicado a la Física y Técnica. Biblioteca Matemática, 1970. págs. 29-30)

Buscamos una solución de la forma u=w(θ)·z(θ)

${\displaystyle \begin{array}{l}w\frac{dz}{d\theta }+z\frac{dw}{d\theta }+2\tan \theta ·(w·z)=\frac{-2b}{g\cos \theta }\\ w\left(\frac{dz}{d\theta }+2\tan \theta ·z\right)+z\frac{dw}{d\theta }=\frac{-2b}{g\cos \theta }\end{array}}$

Hacemos que

${\displaystyle \frac{dz}{d\theta }+2\tan \theta ·z=0}$

La integral se calcula fácilmente

${\displaystyle \begin{array}{l}\frac{dz}{z}=-2\tan \theta {\displaystyle \int \frac{dz}{z}}=-2{\displaystyle \int \tan \theta ·d\theta }\\ \ln z=2\ln \cos \theta +\ln C\\ z=C_1{\cos }^2\theta \end{array}}$

Nos queda ahora que

${\displaystyle \begin{array}{l}z\frac{dw}{d\theta }=\frac{-2b}{g\cos \theta }\frac{dw}{d\theta }=\frac{-2b}{C_{1}g{\cos }^3\theta }\\ w=\frac{-2b}{C_{1}g}{\displaystyle \int \frac{d\theta }{{\cos }^3\theta }}\end{array}}$

Integramos por partes

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{d\theta }{{\cos }^3\theta }=\frac{\tan \theta }{\cos \theta }}-{\displaystyle \int \frac{d\theta }{{\cos }^3\theta }+{\displaystyle \int \frac{d\theta }{\cos \theta }}}\\ {\displaystyle \int \frac{d\theta }{{\cos }^3\theta }=\frac{1}{2}\frac{\tan \theta }{\cos \theta }}+\frac{1}{2}{\displaystyle \int \frac{d\theta }{\cos \theta }}\end{array}}$  

Resolvemos esta última integral haciendo el cambio de variable t=tan(θ/2)

${\displaystyle \begin{array}{l}\cos \theta ={\cos }^2(\theta /2)-{\sin }^2(\theta /2)=\frac{1}{1+t^2}-\frac{t^2}{1+t^2}=\frac{1-t^2}{1+t^2}\\ d\theta =\frac{2}{1+t^2}dt\\ {\displaystyle \int \frac{d\theta }{\cos \theta }}={\displaystyle \int \frac{2dt}{1-t^2}=}{\displaystyle \int \frac{dt}{1-t}}+{\displaystyle \int \frac{dt}{1+t}=}\ln \frac{1+t}{1-t}=\\ \ln \frac{1+\tan (\theta /2)}{1-\tan (\theta /2)}=\ln \frac{\cos (\theta /2)+\sin (\theta /2)}{\cos (\theta /2)-\sin (\theta /2)}=\ln \frac{1+\sin \theta }{\cos \theta }\\ {\displaystyle \int \frac{d\theta }{\cos \theta }}=\ln \left|\tan \theta +\frac{1}{\cos \theta }\right|\end{array}}$

De este modo,

${\displaystyle {\displaystyle \int \frac{d\theta }{{\cos }^3\theta }}=\frac{1}{2}\frac{\tan \theta }{\cos \theta }+\frac{1}{2}\ln \left|\tan \theta +\frac{1}{\cos \theta }\right|}$

Finalmente,

${\displaystyle \begin{array}{l}w=\frac{-2b}{C_{1}g}\left(\frac{1}{2}\frac{\tan \theta }{\cos \theta }+\frac{1}{2}\ln \left|\tan \theta +\frac{1}{\cos \theta }\right|\right)+C_2\\ u=w·z={\cos }^2\theta \left\{C_2-\frac{b}{g}\left(\frac{\tan \theta }{\cos \theta }+\ln \left|\tan \theta +\frac{1}{\cos \theta }\right|\right)\right\}\\ v^2=\frac{1}{{\cos }^2\theta }{\left\{C_2-\frac{b}{g}\left(\frac{\tan \theta }{\cos \theta }+\ln \left|\tan \theta +\frac{1}{\cos \theta }\right|\right)\right\}}^{-1}\end{array}}$

La constante de integración C₂ se calcula a partir de las condiciones iniciales: en el instante t=0, la velocidad de disparo es v₀ y hace un ángulo θ₀ con la horizontal (véase la figura más abajo)

${\displaystyle \begin{array}{l}{v}^2=\frac{1}{{\cos }^2\theta }{\left\{C_2-\frac{b}{g}\left(\frac{\tan \theta }{\cos \theta }+\ln \left|\tan \theta +\frac{1}{\cos \theta }\right|\right)\right\}}^{-1}\\ v_0^2=\frac{1}{{\cos }^2{\theta }_0}{\left\{C_2-\frac{b}{g}\left(\frac{\tan {\theta }_0}{\cos {\theta }_0}+\ln \left|\tan {\theta }_0+\frac{1}{\cos {\theta }_0}\right|\right)\right\}}^{-1}\end{array}}$

La función que relaciona el módulo de la velocidad v y el ángulo θ, que forma la dirección de la velocidad (tangente a la trayectoria) con la horizontal es

${\displaystyle \begin{array}{l}{v}^2=\frac{1}{{\cos }^2\theta }{\left\{\frac{1}{v_{0x}^2}-\frac{b}{g}\left(f(\theta )-f({\theta }_0)\right)\right\}}^{-1}\\ f(\theta )=\frac{\tan \theta }{\cos \theta }+\ln \left|\tan \theta +\frac{1}{\cos \theta }\right|\end{array}}$

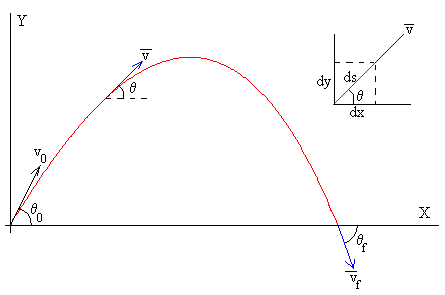
Posición del proyectil

dx=ds·cosθ=ρdθ·cosθ

Utilizando la ecuación del movimiento en la dirección normal, y teniendo en cuenta que la trayectoria tiene curvatura negativa

${\displaystyle \begin{array}{l}dx=-\frac{v^2}{g\cos \theta }\cos \theta ·d\theta =-\frac{v^2}{g}d\theta \\ x=-{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\frac{v^2}{g}d\theta }\end{array}}$

Del mismo modo

dy=ds·sinθ=ρdθ·sinθ

${\displaystyle \begin{array}{l}dy=-\frac{v^2}{g\cos \theta }\sin \theta ·d\theta =-\frac{v^2}{g}\tan \theta d\theta \\ y=-{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\frac{v^2}{g}\tan \theta ·d\theta }\end{array}}$

Tiempo de vuelo

ds=v·dt
ρdθ= v·dt

${\displaystyle \begin{array}{l}dt=-\frac{v^2}{vg\cos \theta }d\theta =-\frac{v}{g\cos \theta }d\theta \\ t=-{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\frac{v}{g\cos \theta }d\theta }\end{array}}$

El programa interactivo calcula el ángulo θ final que forma la dirección de la velocidad cuando y=0 (véase la figura más arriba).

${\displaystyle {\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\frac{v^2}{g}\tan \theta ·d\theta }=0}$

Conocido el ángulo final θ_f se calcula el alcance x y el tiempo de vuelo t, resolviendo numéricamente las integrales

${\displaystyle x=-{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\frac{v^2}{g}d\theta }t=-{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\frac{v}{g\cos \theta }d\theta }}$

Actividades

Se introduce

• El valor del parámetro b

• La velocidad inicial de disparo v₀

• El ángulo de tiro θ

Se pulsa el botón titulado Calcular

El programa interactivo, calcula

• el alcance .

• el tiempo de vuelo

• la altura máxima

Entre paréntesis se muestran los resultados para el caso del tiro parabólico ideal (sin rozamiento)

ForzadasApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Erlichson H. Maximum projectile range with drag and lift, with particular application to golf. Am. J. Phys. 51 (4) April 1983, pp. 357-362.

Warburton R. D. H. , Wang J., Analysis of asymptotic projectile motion with air resistance using Lambert W function. Am. J. Phys. 72 (11) November 2004, pp. 1404-1407

Brancazio P. J. Looking into Chapman's homer: The physics of judging a fly ball. Am. J. Phys. 53 (9) September 1985, pp. 849-855.

Curso Interactivo de Física en Internet © Ángel Franco García