Tiro parabólico con rozamiento

En la página anterior "Movimiento vertical de una esfera en el seno de un fluido" hemos estudiado el movimiento de un objeto lanzado verticalmente hacia arriba en un medio que opone resistencia a su movimiento y lo comparamos con el movimiento del mismo cuerpo en el vacío.

Aplicamos dos modelos de fuerza para describir la resistencia que opone el medio al movimiento del cuerpo.

Una fuerza de rozamiento proporcional a la velocidad, para bajos valores del número de Reynolds

Una fuerza de rozamiento proporcional al cuadrado de la velocidad para altos números de Reynolds.

En esta página, vamos a estudiar el movimiento de proyectiles disparados con la misma velocidad inicial v₀ pero con ángulos de tiro θ distintos.

Como hemos visto en la página "Movimiento bajo la aceleración constante de la gravedad" el proyectil disparado en el vacío con un ángulo de θ =45º tiene un alcance máximo. Vamos a comprobar si esta afirmación se mantiene cuando el proyectil (por ejemplo, una pelota de golf) se mueve en un medio como el aire.

Fuerza de rozamiento proporcional a la velocidad

Si despreciamos el empuje, las fuerzas que actúan sobre el cuerpo de masa m son:

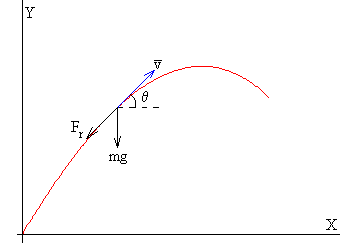
El peso mg
La fuerza de rozamiento F_r, que es sentido contrario al vector velocidad (tangente a la trayectoria). F_r=-mbv.

Las ecuaciones del movimiento del cuerpo serán por tanto.

$\begin{array}{l} m \frac{d v_{x}}{d t} = - m b v_{x} \\ m \frac{d v_{y}}{d t} = - m g - m b v_{y} \end{array}$

La solución de estas ecuaciones con las condiciones iniciales t=0, v_x=v_0x, v_y=v_0y, son

$\begin{array}{l} \frac{d x}{d t} = v_{0 x} \exp (- b t) \\ \frac{d y}{d t} = (\frac{g}{b} + v_{0 y}) \exp (- b t) - \frac{g}{b} \end{array}$

Integrando de nuevo, con las condiciones iniciales t=0, x=0, y=0, tenemos

$\begin{array}{l} x = \frac{v_{0 x}}{b} (1 - \exp (- b t)) \\ y = \frac{1}{b} (\frac{g}{b} + v_{0 y}) (1 - \exp (- b t)) - \frac{g}{b} t \end{array}$

Para un proyectil disparado con velocidad v₀ y ángulo de tiro θ . Las velocidades iniciales son

v_0x=v₀·cosθ
v_0y=v₀·sinθ

Alcance del proyectil, altura máxima y tiempo de vuelo

El proyectil llega al suelo y=0, a una distancia x=R del origen. R se denomina alcance del proyectil.

En la primera ecuación ponemos x=R y despejamos el tiempo de vuelo t,

$t = - \frac{1}{b} \ln (1 - \frac{R b}{v_{0 x}})$

sustituyéndola en la segunda ecuación con y=0.

$(\frac{g}{b} + v_{0 y}) \frac{R}{v_{0 x}} + \frac{g}{b^{2}} \ln (1 - \frac{R b}{v_{0 x}}) = 0$ (1)

Una ecuación trascendente en R, que se resolverá por procedimientos numéricos

La altura máxima, como v_y=dy/dt=0, despejamos el tiempo t y se introduce en la expresión de y

$t = \frac{1}{b} \ln (1 + \frac{b v_{0 y}}{g}) y = \frac{v_{0 y}}{b} - \frac{g}{b^{2}} \ln (1 + \frac{b v_{0 y}}{g})$

Actividades

Se introduce

El valor del parámetro b
La velocidad inicial de disparo v₀
El ángulo de tiro θ

Se pulsa el botón titulado Calcular

El programa interactivo, calcula el alcance R, resolviendo la ecuación trascendente por el método del punto medio. Cuando el parámetro b es grande el procedimiento numérico no produce buenos resultados
Calcula el tiempo de vuelo
La altura máxima

Entre paréntesis se muestran los resultados para el caso del tiro parabólico ideal (sin rozamiento)

Nota: para valores grandes de b: 0.2, 0.3, etc, el procedimiento numérico no produce buenos resultados. Compárese con las trayectorias de la partícula para distintos ángulos de tiro, en al applet más abajo

ForzadasApplet aparecerá en un explorador compatible con JDK 1.1.

Cuando hay rozamiento, el alcance máximo no se obtiene para 45º, sino para un ángulo ligeramente inferior. Calcular el alcance para 45º, 44º, 43º...

Aproximaciones

Si la resistencia del aire es pequeña b~0, el término ln(1-bR/v_0x) se puede desarrollar en serie hasta potencias de tercer orden en b en la ecuación trascendente (1)

$\begin{array}{l} \ln (1 - \frac{b R}{v_{0 x}}) \approx \ln (1) + {\frac{1}{1!} \frac{- R / v_{0 x}}{1 - b R / v_{0 x}} |}_{b = 0} b + {\frac{1}{2!} \frac{- R^{2} / v_{0 x}^{2}}{{(1 - b R / v_{0 x})}^{2}} |}_{b = 0} b^{2} + {\frac{1}{3!} \frac{- 2 R^{3} / v_{0 x}^{3}}{{(1 - b R / v_{0 x})}^{3}} |}_{b = 0} b^{3} = \\ - \frac{R}{v_{0 x}} b - \frac{1}{2} \frac{R^{2}}{v_{0 x}^{2}} b^{2} - \frac{1}{3} \frac{R^{3}}{v_{0 x}^{3}} b^{3} \end{array}$

Haciendo algunas operaciones obtenemos la ecuación de segundo grado en R

$\frac{2 b}{3 v_{0} \cos θ} R^{2} + R - R_{0} = 0 R_{0} = \frac{2 v_{0 x} v_{0 y}}{g}$

Donde R₀ es el alcance cuando no se considera el rozamiento del aire.

Ejemplo: Sea v₀=60 m/s. y θ=45º

Cuando no se considera rozamiento el alcance es

$R_{0} = \frac{v_{0}^{2} \sin (2 θ)}{g} = \frac{60^{2} \sin 90}{9.8} = 367.3 m$

Cuando hay un pequeño rozamiento con el aire b=0.01, el alcance se obtiene resolviendo la ecuación de segundo grado en R, cuya raíz positiva es R=348.3 m

Actividades

Se introduce:

El valor del parámetro b en unidades s^-1, el control de edición titulado b
La velocidad inicial v₀ en el control de edición titulado Velocidad inicial.

Se pulsa el botón titulado Empieza

El programa interactivo traza las trayectorias y calcula el alcance de los proyectiles disparados con ángulos de 10, 15, 20, 25, 30, 35, 40 y 45º (en color rojo)

Compara estas trayectorias con la que seguiría el mismo proyectil disparado con un ángulo de 45º en el vacío (en color azul).

En la parte superior derecha del applet, se muestra el alcance R de cada uno de los proyectiles que se ha calculado resolviendo la ecuación trascendente en R. Podemos observar que el máximo alcance no se obtiene para el ángulo de disparo de 45º sino para un ángulo inferior. Y como cabía esperar, el alcance del proyectil disparado con 45º es inferior en un medio como el aire que en el vacío.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.