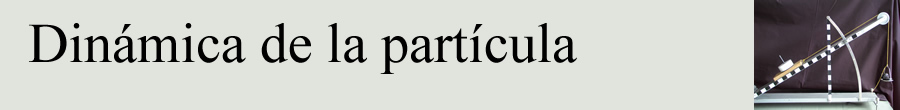El mejor ángulo para arrastrar un bloque

La fuerza de rozamiento

Las fuerzas que actúan sobre el bloque son:

El peso mg
La fuerza aplicada T que forma un ángulo θ con la horizontal.
La fuerza N que ejerce el plano sobre el bloque
La fuerza de rozamiento F_r.

Las condiciones de equilibrio se escriben

Tcosθ-F_r=0
Tsinθ+N-mg=0

Dado el valor de la fuerza aplicada T, podemos calcular la fuerza de rozamiento F_ry la fuerza N que ejerce el plano sobre el bloque:

N=mg-Tsinθ

La reacción N de la superficie horizontal se anula, es decir, el cuerpo se eleva sobre la superficie, si Tsinθ≥mg. Si N>0 la fuerza de rozamiento F_r tiene uno u otro de los siguientes valores:

Si T·cosθ <μ_s(mg-Tsinθ), el cuerpo está en reposo, y F_r=T·cosθ
Si T·cosθ ≥μ_s(mg-Tsinθ), el cuerpo desliza, y F_r=μ_k(mg-Tsinθ)

Siendo μ_s el coeficiente estático de rozamiento

Actividades:

Se introduce

El coeficiente de rozamiento estático μ_s, actuando en la barra de desplazamiento titulada Coef. estático.
El valor del cociente f=T/mg en el control de edición titulado Fuerza/peso
El coeficiente de rozamiento cinético μ_k se ha tomado arbitrariamente igual a μ_s/2.

Se pulsa el botón titulado Dibuja.

En la parte inferior del applet, hay un pequeño cuadrado de color rojo que se puede arrastrar con el puntero del ratón hacia la izquierda o hacia la derecha. Al moverlo, el programa interactivo nos proporciona el valor de la fuerza de rozamiento f_r=F_r/mg para cada valor del ángulo θ seleccionado.

Para evitar que la reacción N sea menor o igual que cero y por tanto, el cuerpo ascienda, se introduce un valor de f=T/mg menor que la unidad.

En la parte superior derecha del applet, se dibujan las fuerzas sobre el bloque y se indica si el cuerpo está en reposo o desliza.

En la figura, se representan tres curvas en función del ángulo θ¸comprendido entre 0º y 90º

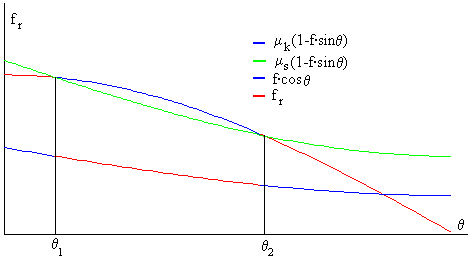
En color azul y rojo, se representa f·cosθ
En color verde, μ_s(1-f·sinθ)
En color azul y rojo, μ_k(1-f·sinθ)
En color rojo, se dibuja el valor de la fuerza de rozamiento f_r, que como vemos es una función discontinua.

Calculamos los ángulos θ para los cuales las curvas f·cosθ y μ_s(1-f·sinθ) se cortan.

f·cosθ =μ_s(1-f·sinθ)

Primero se divide por cosθ, a continuación se emplea la relación 1/cos²θ=1+tan²θ. Quedando la siguiente ecuación en x=tanθ.

$μ_{s} \sqrt{1 + x^{2}} = f + μ_{s} f x$

Elevando al cuadrado ambos miembros, nos queda una ecuación de segundo grado cuyas soluciones son

$\tan θ = x = \frac{- f^{2} \pm \sqrt{μ_{s}^{2} f^{2} + f^{2} - μ_{s}^{2}}}{μ_{s} (f^{2} - 1)}$

Pueden ocurrir los siguientes casos:

Cuando el discriminante es negativo, no hay ninguna raíz

f·cosθ <μ_s(1-f·sinθ) para todos los ángulos θ

Ejemplo 1:

Sea μ_s=0.6 y f=0.5,

Comprobamos que el discriminante vale -0.02 es negativo.

Observamos en el applet, que la curva de color verde μ_s(1-f·sinθ) se mantiene por encima de la curva de color rojo f·cosθ, el cuerpo siempre está en reposo y la fuerza de rozamiento vale f_r= f·cosθ

Cuando el discriminante es nulo

$μ_{s}^{2} f^{2} + f^{2} - μ_{s}^{2} = 0 f = \frac{μ_{s}}{\sqrt{1 + μ_{s}^{2}}}$

La raíz doble de la ecuación de segundo grado vale

tanθ=x= μ_s

Ejemplo 2:

Sea μ_s=0.6, calculamos e introducimos el valor de f=0.514

Observamos en el applet, que la curva de color verde μ_s(1-f·sinθ) se mantiene por encima de la curva de color rojo f·cosθ, tocándose para el ángulo θ=31º. El cuerpo está en reposo, la fuerza de rozamiento vale f_r= f·cosθ. Justamente para este único ángulo el cuerpo empieza a deslizar y la fuerza de rozamiento disminuye al valor μ_k(1-f·sinθ)

Cuando el discriminante es positivo

Tenemos dos raíces x₁ y x₂ que corresponden a los ángulos θ₁ y θ₂, una de ellas es siempre positiva, la otra puede ser positiva o negativa. Supongamos que ambas son positivas tal como se aprecia en la figura,.más arriba

Ejemplo 3:

Sea μ_s=0.6, e incrementamos la fuerza f=0.55

Calculamos las raíces de la ecuación de segundo grado x₁ y x₂ y los ángulos correspondientes θ₁=10.26 y θ₂=51.66,

En la región 0< θ< θ₁

f·cosθ es menor que μ_s(1-f·sinθ), el cuerpo permanece en reposo y la fuerza de rozamiento es f_r= f·cosθ

En la región θ₁≤ θ≤ θ₂

f·cosθ es mayor que μ_s(1-f·sinθ), el cuerpo desliza y la fuerza de rozamiento f_r disminuye al valor μ_k(1-f·sinθ)

En la región θ₂< θ< 90º

f·cosθ es menor que μ_s(1-f·sinθ), el cuerpo permanece en reposo, y la fuerza de rozamiento vale f_r= f·cosθ

Por tanto, en el intervalo angular (θ₁≤ θ≤ θ₂) el cuerpo desliza, para el resto de los ángulos el cuerpo permanece en reposo.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Arrastre con el puntero del ratón el pequeño cuadrado de color rojo

Referencias

Sütt D. Elementary discussion of an optimization problem concerning friction. Physics Education 29 (4) July 1994, 249-252

van den Berg W. The best angle for dragging a box. The Physics Teacher, Vol. 38 Nov. 2000, pp. 506-508