Movimiento del c.m. y de las partículas de un sistema (I)

Esta página y las dos siguientes se estudia un sistema formado por dos partículas unidas por un muelle elástico que tratarán de ayudar a reconocer:

Cuáles son las fuerzas interiores o de interacción entre las partículas del sistema.
Cuáles son las fuerzas exteriores que actúan sobre cada una de las partículas.
Qué fuerzas determinan el movimiento de cada unas de las partículas.
Qué fuerzas determinan el movimiento del c.m. del sistema de partículas.

Veremos que el movimiento de cada partícula está determinado por la acción de las fuerzas exteriores al sistema y de las fuerzas de interacción de las otras partículas del sistema sobre la partícula considerada.

Combinaremos las dos ecuaciones del movimiento para obtener:

la ecuación del movimiento del centro de masas del sistema de partículas que se mueve como si fuera una partícula de masa igual a la masa total del sistema bajo la acción de la resultante de las fuerzas exteriores aplicadas al sistema.
el movimiento relativo de las dos partículas depende solamente de las fuerzas interiores o de interacción entre las dos partículas.

Estas dos ecuaciones son fácilmente integrables, y nos permiten obtener la posición y velocidad de cada una de las partículas en función del tiempo.

Otros aspectos interesantes que se podrán estudiar son:

El principio de conservación de la energía aplicado a un sistema de partículas
La relación entre impulso de las fuerzas exteriores y variación del momento lineal del sistema.

Descripción

Consideremos un sistema simple de partículas consistente en un muelle en posición vertical que tiene una masa M en el extremo superior y una masa m en su extremo inferior. Se supone que la masa del muelle es despreciable. Inicialmente, el muelle de constante k, está en equilibrio sujeto por la masa M tal como se muestra en la figura.

Situación inicial:

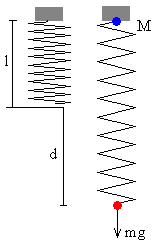Si l es la longitud del muelle sin deformar, cuando se cuelga de su extremo inferior una masa m, la longitud del muelle se incrementa en d

mg=kd

Para analizar el problema, estableceremos el origen, en la posición inicial de la partícula de masa M, y consideraremos positivas las distancias medidas en sentido descendente.

Ecuación del movimiento de cada una de las partículas:

Cuando se libera el muelle, al cabo de un cierto tiempo t, la posición de la masa inferior m es x y el de la masa superior M es y. Aplicando las leyes de la dinámica a cada una de las partículas vamos a calcular sus posiciones x e y en función del tiempo t.

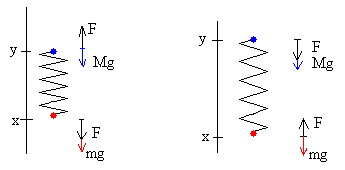
La deformación del muelle en el instante t es l-(x-y) y la fuerza que ejerce el muelle sobre cada una de las partículas es F=k·(l-x+y).

Cuando el muelle está comprimido l>(x-y), la fuerza F=k(l-x+y) es positiva (figura de la izquierda).
Cuando el muelle está estirado l<(x-y), la fuerza F=k(l-x+y) es negativa (figura de la derecha).

Movimiento de la partícula de masa m

$m \frac{d^{2} x}{d t^{2}} = m g + k (l - x + y)$

Condiciones iniciales: para t=0 su velocidad inicial es cero dx/dt=0 y se encuentra en x=l+d

Movimiento de la partícula de masa M

$M \frac{d^{2} y}{d t^{2}} = M g - k (l - x + y)$

Condiciones iniciales: para t=0, su velocidad inicial es cero dy/dt=0 y se encuentra en el origen y=0.

Movimiento del centro de masa del sistema de dos partículas

La posición del centro de masas del sistema de dos partículas es

$z = \frac{m x + M y}{m + M}$

Sumando miembro a miembro las dos ecuaciones diferenciales, llegamos a la ecuación del movimiento del c.m. del sistema

$(m + M) \frac{d^{2} z}{d t^{2}} = m g + M g$

El centro de masas de un sistema de partículas se mueve como si fuera una partícula de masa igual a la masa total del sistema bajo la acción de la resultante de las fuerzas exteriores aplicadas al sistema.

Las condiciones iniciales son: en el instante t=0, la velocidad inicial del c.m. es cero y se encuentra en z₀, cuando el muelle estaba sujeto por la parte superior, x=l+d, y=0.

$z_{0} = \frac{m (l + d)}{m + M} = \frac{m (k l + m g)}{k (m + M)}$

La aceleración del centro de masas es constante e igual a g. La posición del centro de masas en función del tiempo, será.

$z = z_{0} + \frac{1}{2} g t^{2}$

Movimiento relativo de las dos partículas

Multiplicando la primera ecuación del movimiento por M, la segunda por m y restando obtenemos

$\begin{array}{l} M (\frac{d^{2} x}{d t^{2}} - \frac{d^{2} y}{d t^{2}}) = (m + M) k (l - x + y) \\ \frac{m M}{m + M} \frac{d^{2} (x - y)}{d t^{2}} = k (l - (x - y)) \end{array}$

Esta última ecuación, nos dice que el movimiento relativo de las dos partículas es equivalente al movimiento de una partícula de masa reducida μ bajo la acción de la fuerza que describe la interacción mutua F=k(l-x+y).

Haciendo el cambio de variable ξ=x-y, tenemos la ecuación diferencial

$μ \frac{d^{2} ξ}{d t^{2}} = k (l - ξ) \frac{d^{2} ξ}{d t^{2}} + \frac{k}{μ} ξ = \frac{k}{μ} l$

La solución de esta ecuación diferencial es

$ξ = l + A \sin (ω t) + B \cos (ω t) ω = \sqrt{\frac{k}{μ}} = \sqrt{\frac{k (m + M)}{m M}}$

Las constantes A y B se determinan a partir de las condiciones iniciales

En el instante t=0, la posición relativa ξ=x-y=l+d, y la velocidad relativa es cero dξ/dt=0. Donde d=mg/k es la deformación inicial del muelle

ξ=l+d·cos(ωt).

Movimiento de cada una de las partículas

Conocida la ecuación del movimiento del centro de masas, y la ecuación del movimiento relativo de las dos partículas, determinamos el movimiento de cada una de las partículas.

$\begin{array}{l} z = \frac{m x + M y}{m + M} = \frac{m (k l + m g)}{k (m + M)} + \frac{1}{2} g t^{2} \\ x - y = l + \frac{m g}{k} \cos (ω t) \end{array}$

Despejamos x e y del sistema de dos ecuaciones,

$\begin{array}{l} z = \frac{m x + M y}{m + M} = \frac{m (k l + m g)}{k (m + M)} + \frac{1}{2} g t^{2} \\ x - y = l + \frac{m g}{k} \cos (ω t) \end{array}$

Como podemos comprobar, en el instante t=0, las posiciones iniciales de las partículas son x=l+mg/k, y=0.

Las velocidades de las partículas se obtienen derivando x e y respecto del tiempo

$\begin{array}{l} \frac{d x}{d t} = g t - ω \frac{M m g}{k (m + M)} \sin (ω t) \\ \frac{d y}{d t} = g t - ω \frac{m^{2} g}{k (m + M)} \sin (ω t) \end{array}$

En el instante t=0, las partículas están en reposo

Energías

Vamos a comprobar que el trabajo de las fuerzas exteriores (el peso) se invierte en modificar la energía del sistema de partículas, W_ext=U_f-U_i, o bien

W_ext=ΔE_k+ ΔE_p

Variación de energía cinética ΔE_k

Como las partículas están inicialmente en reposo, la variación de energía cinética del sistema formado por las dos partículas es igual a la energía cinética final.

$Δ E_{k} = \frac{1}{2} m {(\frac{d x}{d t})}^{2} + \frac{1}{2} M {(\frac{d y}{d t})}^{2} = \frac{1}{2} (m + M) g^{2} t^{2} + \frac{1}{2} \frac{m^{2} g^{2}}{k} \sin^{2} (ω t)$

Variación de energía potencial ΔE_p

En la situación inicial, el muelle está deformado una longitud d.

En la situación final, la deformación del muelle es l-x+y.

La variación de energía potencial es

$Δ E_{p} = \frac{1}{2} k {(l - x + y)}^{2} - \frac{1}{2} k d^{2} = \frac{1}{2} \frac{m^{2} g^{2}}{k} \cos^{2} (ω t) - \frac{1}{2} \frac{m^{2} g^{2}}{k}$

El trabajo de la fuerza exterior W_ext

El trabajo es el producto de la fuerza (m+M)g por el desplazamiento del c.m. (z-z₀).

$W_{e x t} = (m + M) g (z - z_{0}) = \frac{1}{2} (m + M) g^{2} t^{2}$

Teniendo en cuanta que sin²(ωt)+ cos²(ωt)=1, vemos que se cumple la ecuación que describe el balance energético para el sistema formado por dos partículas unidas por un muelle elástico.

Levitación de la partícula inferior

Podemos observar que en los primeros instantes del movimiento, la partícula superior (de color azul) y el centro de masa (de color negro) se desplazan, pero la partícula inferior (de color rojo) apenas cambia su posición, parece estar suspendida durante unos instantes en el aire, tal como se puede observar en la figura y el el applet.

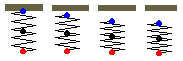
En la ecuación que nos da la posición x de la partícula inferior, supongamos que ω t es pequeño, cos(ω t)≈1

x≈l+mg/k=l+d

La posición de la partícula inferior cambia muy poco en los primeros instantes del movimiento. En la gráfica de la posición x en función del tiempo t, a la derecha en el applet, observamos un pequeño segmento horizontal de color rojo.

Actividades

Se introduce:

La masa M de la partícula superior, en el control de edición titulado Masa superior.
La masa m de la partícula inferior, en el control de edición titulado Masa inferior.
La constante k del muelle elástico, en el control de edición titulado Constante muelle.
La longitud del muelle sin deformar se ha fijado en el programa en l=1 m.

Se pulsa el botón titulado Empieza.

Observamos el movimiento de cada una de las dos partículas y la del centro de masa del sistema (en color negro). A la derecha, se representa su posición (altura) en función del tiempo t.

El programa verifica los datos que introduce el usuario de modo que la deformación máxima del muelle no pueda ser mayor que su longitud inicial l.

Ejemplo:

Se introduce

m=4 kg
M=1 kg
k=50 N/m
La longitud inicial del muelle sin deformar es l=1.0 m

Calcular las posiciones de las partículas y la del centro de masa en el instante t=1 s.

$ω = \sqrt{\frac{50 (1 + 4)}{1 \cdot 4}} = 7.9 rad/s$

Las posiciones de las partículas son

$\begin{array}{l} x = 1.0 + \frac{1}{2} 9.8 \cdot 1^{2} + 4 \cdot 9.8 \frac{4 + 1 \cdot \cos (7.9 \cdot 1)}{50 (4 + 1)} = 6.52 m \\ y = \frac{1}{2} 9.8 \cdot 1^{2} + \frac{4^{2} \cdot 9.8}{50 (4 + 1)} (1 - \cos (7.9 \cdot 1)) = 5.56 m \end{array}$

Conocida la posición de las partículas de masas m=4 y M=1 kg calculamos la posición del c.m.

$z = \frac{4 \cdot 6.52 + 1 \cdot 5.56}{4 + 1} = 6.33 m$

La posición inicial del centro de masa es

$z_{0} = \frac{4 (50 \cdot 1 + 4 \cdot 9.8)}{50 (4 + 1)} = 1.43 m$

La posición del c.m. en el instante t=1 es

$z = 1.43 + \frac{1}{2} 9.8 \cdot 1^{2} = 6.33 m$

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Glaister. Oscillations of a falling spring. Phys. Educ. V-28 (5) 1993, pp. 329-33