• Inicio
• Dinámica
• Trabajo y energía

Radio de curvatura

En el lenguaje ordinario, decimos que un trozo de carretera Δs tiene más curvatura que otro cuando el cambio de dirección Δθ es mayor a igualdad de camino recorrido en ambos. Compárese la figura de la izquierda con la de la derecha

El radio ρ de curvatura medio e instantáneo se definen, respectivamente,

${\displaystyle <\rho >=\frac{\Delta s}{\Delta \theta }\rho =\underset{\Delta s\to 0}{\lim }\frac{\Delta s}{\Delta \theta }=\frac{ds}{d\theta }}$

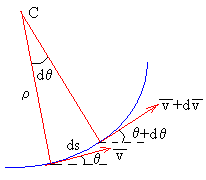El radio de curvatura ρ  y el centro C de curvatura se determinan del siguiente modo: Se traza la tangente a un punto de la trayectoria y a continuación, se traza la normal. Se toma un punto muy próximo al anterior, se traza la tangente y la normal en dicho punto.

Las normales se cortan en un punto denominado centro de curvatura C, y la distancia de C a uno u otro punto de la trayectoria, infinitamente próximos entre sí, se denomina radio de curvatura ρ.

Si el ángulo comprendido entre las dos tangentes es dθ, este es el ángulo que forman las dos normales. La longitud del arco entre los dos puntos considerados es ds=ρ·dθ .

Dada la función y=f(x), vamos a determinar la fórmula que nos permite calcular el radio de curvatura ρ de la curva en la posición de abscisa x.

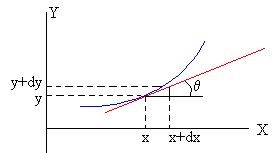Como vemos en la figura, en el triángulo rectángulo de base dx, altura dy e hipotenusa ds, establecemos las siguientes relaciones

${\displaystyle \tan \theta =\frac{dy}{dx}ds=\sqrt{d{x}^2+d{y}^2}=\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}$

 

 

 

La fórmula del radio de curvatura es

${\displaystyle \rho =\frac{ds}{d\theta }=\frac{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}{d\arctan \frac{dy}{dx}}=\frac{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}{\frac{\frac{d^{2}y}{d{x}^2}dx}{1+{\left(\frac{dy}{dx}\right)}^2}}=\frac{{\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}^{3/2}}{\frac{d^{2}y}{d{x}^2}}}$

El radio de curvatura es una cantidad positiva

Referencia

Puig Adam P. Cálculo Integral Aplicado a la Física y Técnica. Biblioteca Matemática, 1972, pág. 286-287

Curso Interactivo de Física en Internet © Ángel Franco García