• Inicio
• Dinámica
• Trabajo y energía

Un bloque desliza a lo largo de un plano inclinado y deforma un muelle

Se suele proponer el siguiente problema a los estudiantes como ejemplo ilustrativo de fuerzas conservativas y no conservativas que actúan sobre un cuerpo.

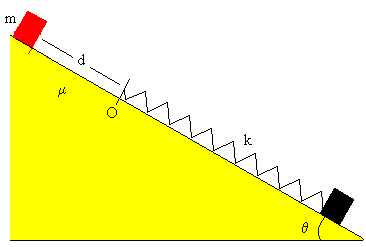
Un bloque de masa m desliza a lo largo de un plano inclinado de ángulo θ. Parte del reposo a una distancia d del muelle elástico sin deformar de constante k. Calcular la máxima deformación del muelle. Se supone que el plano no es liso, sino que ejerce una fuerza de rozamiento de coeficiente μ_k sobre el bloque que desliza a lo largo del mismo.

Comparamos la situación inicial y la situación final

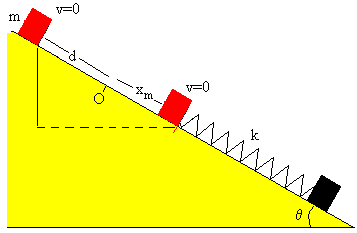
Situamos el nivel cero de energía potencial en el origen O. El trabajo de la fuerza de rozamiento es igual a la diferencia entre la energía inicial y la energía final

${\displaystyle \begin{array}{l}-f_r(x_m+d)=\left(\frac{1}{2}k{x}_m^2-mg{x}_m\sin \theta \right)-mgd\sin \theta \\ f_r=-{\mu }_{k}mg\cos \theta \end{array}}$

Por ejemplo, si d=1.0 m, θ=30º, μ=0.3, k=50 N/m, m=1.0 kg

Resolvemos la ecuación de segundo grado en x_m y tomamos la raíz positiva x_m=0.357 m=35.7 cm

El problema, como vamos a ver a lo largo de esta página, es susceptible de un estudio más detallado

Ecuaciones del movimiento

Para analizar el movimiento, situamos el eje X a lo largo  del plano inclinado, con el origen en la posición del extremos libre del muelle sin deformar, la parte positiva apuntando hacia abajo. Las etapas del movimiento son las siguientes:

1.-El bloque baja deslizando por el plano inclinado

El bloque parte de la posición x₀<0 y desliza hacia abajo si la componente del peso mg·sinθ es mayor que la fuerza de rozamiento máxima, μ_s·mg·cosθ, en caso contrario, permanecerá en reposo en la posición inicial.

mgsinθ≥μ_s·mg·cosθ

El ángulo θ del plano inclinado para que el bloque deslice tiene valer tanθ≥μ_s

Supongamos que se cumple esta condición y el bloque desliza hacia abajo. Las fueras sobre el bloque son:

• El peso mg

• La reacción del plano N=mg·cosθ

• La fuerza de rozamiento, de sentido contrario a la velocidad del bloque f_r=μ_k·N

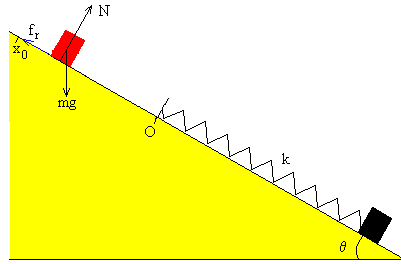
La aceleración constante es

a₊₌g(sinθ-μcosθ)

La posición x y velocidad v en función del tiempo es

${\displaystyle x=x_0+\frac{1}{2}{a}_{+}{t}^{2}v=a_{+}t}$

Llega al origen en el instante t con velocidad v₀.

${\displaystyle t=\sqrt{\frac{-2x_0}{a_{+}}}{v}_0=\sqrt{-2a_{+}{x}_0}}$

2.-El bloque en contacto con el muelle, desliza hacia abajo

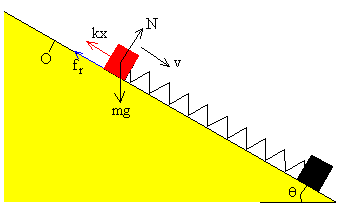Las fuerzas sobre el bloque son:

• El peso mg

• La reacción del plano N=mg·cosθ

• La fuerza que ejerce el muelle deformado x,  k·x

• La fuerza de rozamiento, de sentido contrario a la velocidad del bloque, f_r=μ_k·N

Cuando el bloque se mueve hacia abajo (v>0), la ecuación del movimiento es

ma=-kx+mgsinθ-μ_kmgcosθ
ma=-kx+ma₊

Escribimos la ecuación del movimiento en forma de ecuación diferencial

${\displaystyle \frac{d^{2}x}{d{t}^2}+{\omega }^{2}x=a_{+}\frac{dx}{dt}>0}$

con ω²=k/m

Esta ecuación del movimiento nos recuerda la ecuación diferencial de un MAS, pero además tiene un término adicional a₊

La solución de la ecuación diferencial es la suma de la homogénea (la ecuación de un MAS) más una constante C. Introduciendo la solución particular (la constante C)  en la ecuación diferencial

ω²C= a₊                  C=a₊ /ω²

La solución completa de la ecuación diferencial es

${\displaystyle x=A\sin (\omega t)+B\cos (\omega t)+\frac{a_{+}}{{\omega }^2}v>0}$

La velocidad del bloque es

${\displaystyle v=\frac{dx}{dt}=A\omega \cos (\omega t)-B\omega \sin (\omega t)}$

Los coeficientes A y B se determinan a partir de las condiciones iniciales

Ponemos el contador de tiempo parcial a cero t=0, el bloque llega al origen x=0, con velocidad v₀.

${\displaystyle 0=B+\frac{a_{+}}{{\omega }^2}{v}_0=A\omega }$

La posición x y la velocidad v del bloque en su movimiento a lo largo del plano inclinado, hacia abajo, es

${\displaystyle \begin{array}{l}x=\frac{v_0}{\omega }\sin (\omega t)+\frac{a_{+}}{{\omega }^2}\left(\text{1-cos}(\omega t)\right)\\ v=v_0\cos (\omega t)+\frac{a_{+}}{\omega }\sin (\omega t)\end{array}}$

El máximo desplazamiento x_m se produce cuando la velocidad es nula v=0, en el instante t tal que

${\displaystyle \tan (\omega t)=-\frac{v_0\omega }{a_{+}}\omega t=\pi -\arctan \left(\frac{v_0\omega }{a_{+}}\right)}$

Teniendo en cuanta las relaciones

${\displaystyle \sin \theta =\frac{\tan \theta }{\sqrt{1+{\tan }^2\theta }}\text{cos}\theta =\frac{1}{\sqrt{1+{\tan }^2\theta }}}$

y que en el segundo cuadrante, el seno es positivo y el coseno es negativo. Llegamos después de algunas operaciones a la expresión para el máximo desplazamiento x_m

${\displaystyle x_m=\frac{\sqrt{v_0^2{\omega }^2+a_{+}^2}+a_{+}}{{\omega }^2}}$

3.-El bloque en contacto con el muelle, desliza hacia arriba

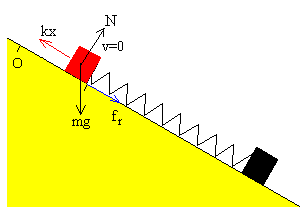El móvil parte de x_m con velocidad inicial nula siempre que se cumpla que

kx_m-mgsinθ ≥ μ_smgcosθ,
ω²x_m≥a_-

en caso contrario la posición x_m será la posición final del bloque.

 

 

 

Supongamos que se cumple la primera condición.

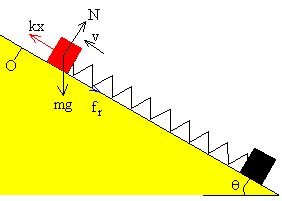Cuando el bloque se desliza a lo largo del plano inclinado, hacia arriba (v<0), la fuerza de rozamiento cambia de sentido y la ecuación del movimiento es

ma=-kx +mgsinθ+μ_kmgcosθ
ma=-kx+ma_-

Escribimos la ecuación del movimiento en forma de ecuación diferencial

${\displaystyle \frac{d^{2}x}{d{t}^2}+{\omega }^{2}x=a_{-}\frac{dx}{dt}<0}$

La solución completa de la ecuación diferencial es

${\displaystyle x=A\sin (\omega t)+B\cos (\omega t)+\frac{a_{-}}{{\omega }^2}v<0}$

Ponemos el contador de tiempo parcial t a cero, el bloque parte de la posición x_m con velocidad nula, las constantes A y B de la ecuación de la posición valen

${\displaystyle x_m=B+\frac{a_{-}}{{\omega }^2}0=A\omega }$

La posición x y la velocidad v de dicho cuerpo en su movimiento a lo largo del plano inclinado, hacia arriba, son

${\displaystyle \begin{array}{l}x=\left(x_m-\frac{a_{-}}{{\omega }^2}\right)\text{cos}(\omega t)+\frac{a_{-}}{{\omega }^2}\\ v=-\left(x_m\omega -\frac{a_{-}}{\omega }\right)\sin (\omega t)\end{array}}$

Cuando el móvil pasa por el origen x=0,

${\displaystyle 0=\left(x_m-\frac{a_{-}}{{\omega }^2}\right)\text{cos}(\omega t)+\frac{a_{-}}{{\omega }^2}\text{cos}(\omega t)=\frac{-a_{-}}{{\omega }^2{x}_m-a_{-}}}$

• Pasa por el origen

Como |cos(ωt)|≤1 se tiene que cumplir que ω²x_m≥2a_-.para pasar por el origen, en el instante t tal que

${\displaystyle \omega t=\pi -\arccos \left(\frac{a_{-}}{{\omega }^2{x}_m-a_{-}}\right)}$

La velocidad v_f que lleva al pasar por el origen x=0 es

${\displaystyle v_f=-\left(x_m\omega -\frac{a_{-}}{\omega }\right)\sin (\omega t)=-\left(x_m\omega -\frac{a_{-}}{\omega }\right)\sqrt{1-{\cos }^2(\omega t)}=-\sqrt{{\omega }^2{x}_m^2-2a_{-}{x}_m}}$

Como el radicando no puede ser negativo se tiene que cumplir que ω²x_m≥2a_-

A continuación, el bloque continúa ascendiendo por el plano inclinado, x<0 sin estar en contacto con el muelle

• No pasa por el origen

En el caso que ω²x_m<2a_- el móvil se para antes de llegar al origen, en el instante t en el que v=0 ó sin(ωt)=0, ωt=π. El móvil se para en la posición

${\displaystyle x_1=\left(x_m-\frac{a_{-}}{{\omega }^2}\right)\text{cos}\pi +\frac{a_{-}}{{\omega }^2}=-x_m+\frac{2a_{-}}{{\omega }^2}}$

En este instante, se completa un ciclo del movimiento del bloque. Puede ocurrir que se pare definitivamente, o descienda por el plano inclinado x>0, tal como analizaremos más adelante

4.-El bloque desliza hacia arriba, x<0

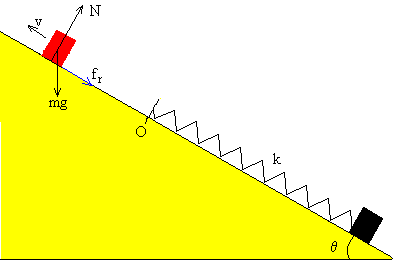Las fuerzas sobre el bloque son:

• El peso mg

• La reacción del plano N=mg·cosθ

• La fuerza de rozamiento, f_r=μ_k·N

La aceleración constante es

a_-=g(sinθ+μcosθ)

El movimiento es rectilíneo, uniformemente acelerado. De nuevo ponemos el contador de tiempo parcial a cero.

v=v_f+a_-t
x=v_f·t+a_-t²/2

Como v_f<0, y a_->0 el bloque se para cuando v=0, en la posición

${\displaystyle x_0=-\frac{v_f^2}{2a_{-}}}$

se completa un ciclo, se vuelve a repetir el movimiento tomando esta posición inicial de partida.

4.-El bloque en contacto con el muelle, desliza hacia abajo

Volverá a deslizar a lo largo del plano inclinado, hacia abajo, si

mgsinθ-kx₁≥μ_k·mgcosθ,
ω²x₁≤a₊.

La solución de la ecuación del movimiento para v>0 es

${\displaystyle \begin{array}{l}x=A\sin (\omega t)+B\cos (\omega t)+\frac{a_{+}}{{\omega }^2}v>0\\ v=\frac{dx}{dt}=A\omega \text{cos}(\omega t)-B\omega \sin (\omega t)\end{array}}$

Ponemos el contador de tiempo parcial a cero. Las condiciones iniciales son t=0, x=x₁y v=0,

${\displaystyle x_1=B+\frac{a_{+}}{{\omega }^2}0=A\omega }$

${\displaystyle x=\left(x_1-\frac{a_{+}}{{\omega }^2}\right)\text{cos}(\omega t)+\frac{a_{+}}{{\omega }^2}v=-\left(x_1\omega -\frac{a_{+}}{\omega }\right)\sin (\omega t)}$

La máxima deformación del muelle, se alcanzará cuando v=0, es decir, en el instante t tal que  sin(ωt)=0, ωt=π. El móvil se detiene en la posición

${\displaystyle x_2=\left(x_1-\frac{a_{+}}{{\omega }^2}\right)\text{cos}\pi +\frac{a_{+}}{{\omega }^2}=-x_1+\frac{2a_{+}}{{\omega }^2}}$

El móvil parte de x₂ con velocidad inicial nula siempre que se cumpla que

kx₂-mgsinθ ≥ μ_smgcosθ,
ω²x₂≤a_-.

en caso contrario la posición x₂ será la posición final del bloque en reposo.

Supongamos que se cumple la primera condición. Ponemos el contador de tiempo parcial a cero. Las condiciones iniciales son t=0, x=x₂, v=0, Tomamos las ecuaciones del movimiento del bloque en contacto con el muelle, hacia arriba. Después de un tiempo t tal que ωt=π. El móvil se para en la posición

${\displaystyle x_3=\left(x_2-\frac{a_{-}}{{\omega }^2}\right)\text{cos}\pi +\frac{a_{-}}{{\omega }^2}=-x_2+\frac{2a_{-}}{{\omega }^2}}$

y así, sucesivamente, hasta que se detiene en una posición x_i>0

Curso Interactivo de Física en Internet © Ángel Franco García