Viaje por el interior de la Tierra

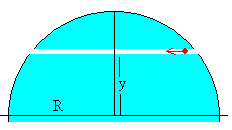Supongamos que excavamos un túnel en la Tierra lo largo de una dirección paralela a uno de sus diámetros tal como se muestra en la figura. En esta página, estudiaremos el movimiento de una partícula que se introduce por uno de los extremos del túnel y demostraremos que tarda un tiempo de 42 minutos en salir por el otro extremo. Este tiempo es independiente de la longitud del túnel.

Se desprecia el rozamiento, y se supone que la Tierra no gira sobre su eje y que es perfectamente esférica, de densidad uniforme, y que el túnel tiene un diámetro suficientemente pequeño para que no afecte a la fuerza de atracción que ejerce la Tierra sobre la partícula considerada.

Podríamos imaginar que se hace un túnel que atraviese la Tierra desde España a sus antípodas situadas en Nueva Zelanda. Una persona que se introdujese en el túnel en Madrid saldría por el extremo opuesto después de 42 minutos de viaje, suponiendo que resista las altas temperaturas existentes en el centro de la Tierra.

Supongamos que se hace un túnel que conecte las ciudades de Bilbao y Madrid, una persona que se introduce en el túnel en ciudad origen llegaría al destino al cabo de 42 minutos, más o menos el tiempo de viaje en avión, sin tener en cuenta la larga espera en el aeropuerto antes del embarque.

Intensidad del campo gravitatorio g producido por la Tierra

En la sección campo eléctrico del capítulo Electromagnetismo, se estudia un caso similar, el modelo de Kelvin-Thomson de un átomo de hidrógeno o ión hidrogenoide con un solo electrón. El átomo tiene forma esférica de radio R, y la carga positiva Q está uniformemente distribuida en dicha esfera.

El campo gravitatorio y el campo eléctrico tienen similitudes y diferencias.

El campo eléctrico está asociado a una propiedad de la materia que es la carga eléctrica. Hay dos tipos de carga positiva y negativa. Las fuerzas que describen las interacciones entre partículas cargadas pueden ser atractivas o repulsivas.
El campo gravitatorio está asociado a una propiedad de la materia que es la masa. La fuerza que describe la interacción entre dos partículas es siempre atractiva.

El campo gravitatorio producido por una distribución esférica de masa de radio R y masa M , tiene una expresión similar al campo eléctrico producido por una distribución esférica de carga de radio R y carga total Q. Para calcular el campo gravitatorio utilizaremos en las siguientes equivalencias fundamentadas en la ley de Gauss.

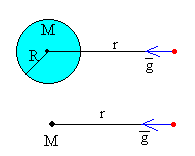
El campo gravitatorio producido por una distribución esférica uniforme de masa M y radio R en un punto distante r>R del centro es equivalente al campo gravitatorio producido por una partícula de masa M situada en el centro de la esfera en un punto distante r de la misma

El campo gravitatorio producido por una distribución esférica uniforme de masa M y de radio R en un punto situado a una distancia r<R del centro, es equivalente al campo gravitatorio producido por la porción de masa contenida en la esfera de radio r en un punto de su superficie.

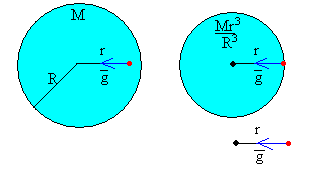
$\frac{M \frac{4}{3} π r^{3}}{\frac{4}{3} π R^{3}} = M \frac{r^{3}}{R^{3}}$

y por tanto, es equivalente al campo gravitatorio producido por una partícula de masa M r³/R³ situada en el centro de la esfera en un punto distante r de la misma.

El campo gravitatorio g producido por una distribución esférica y uniforme de masa de radio R y masa M tiene dirección radial y sentido hacia el centro de la Tierra. Su módulo vale.

$g = G \frac{M}{r^{2}} r > R g = G \frac{M r}{R^{3}} r < R$

Túnel por el interior de la Tierra

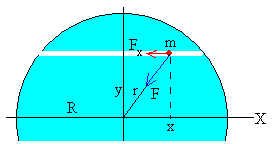La fuerza F sobre la partícula de masa m situada a una distancia r<R del centro de la Tierra vale

$F = m g = G \frac{M m}{R^{3}} r$

La componente de dicha fuerza F_x a lo largo del eje del túnel es

$F_{x} = - F \frac{x}{r} = - G \frac{M m}{R^{3}} x$

La fuerza F_x es proporcional al desplazamiento x de la partícula respecto de la posición de equilibrio estable (F_x=0) y de sentido contrario al mismo, un signo inequívoco de que la partícula describe un Movimiento Armónico Simple (M.A.S.).

La ecuación del movimiento es

$\begin{array}{l} m \frac{d^{2} x}{d t^{2}} = - G \frac{M m}{R^{3}} x \\ \frac{d^{2} x}{d t^{2}} + G \frac{M}{R^{3}} x = 0 \end{array}$

Llegamos a la ecuación diferencial de un MAS de periodo P=2π/ω

$P = 2 π \sqrt{\frac{R^{3}}{G M}} = 2 π \sqrt{\frac{{(6.37 \cdot 10^{6})}^{3}}{6.67 \cdot 10^{- 11} \cdot 5.98 \cdot 10^{24}}} = 5057.96 s = 84.3 min$

La partícula describe un MAS cuyo periodo es de 84.3 minutos y es independiente de la amplitud.

Movimiento sobre una superficie horizontal

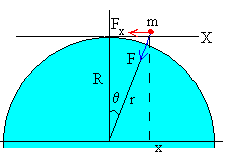Supongamos una partícula de masa m que desliza sin rozamiento a lo largo de una superficie horizontal (tangente a la superficie de la Tierra), tal como se muestra en la figura.

La fuerza sobre la partícula vale

$F = G \frac{M m}{r^{2}}$

La componente de dicha fuerza F_x=-F·sinθ=-F·x/r es de sentido contrario al desplazamiento pero ya no es proporcional al desplazamiento x sino a x/r³

La ecuación del movimiento de la partícula será ahora

$\frac{d^{2} x}{d t^{2}} + G \frac{M}{r^{3}} x = 0$

Si el desplazamiento x es pequeño, o el ángulo θ es pequeño, podemos hacer la aproximación r≈R. La partícula describe un MAS cuyo periodo es de nuevo 84.3 minutos siempre que la amplitud sea pequeña.

Como en el péndulo simple, el periodo de las oscilaciones es dependiente de la amplitud, y se puede considerar constante en la aproximación de pequeñas desviaciones de la posición de equilibrio estable.

Orbita circular alrededor de la Tierra

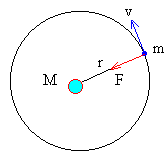Aplicando la ecuación de la dinámica del movimiento circular, obtenemos la velocidad v de un cuerpo de masa m que describe una órbita circular de radio r alrededor de la Tierra es

$G \frac{M m}{r^{2}} = m \frac{v^{2}}{r}$

El tiempo que tarda en dar una vuelta completa o periodo es

$P = \frac{2 π r}{v} = 2 π \sqrt{\frac{r^{3}}{G M}}$

Los cuadrados de los periodos son proporcionales a los cubos de el radio de la trayectoria circular (tercera ley de Kepler).

Supongamos que la Tierra es perfectamente esférica, sin accidentes geográficos, y sin atmósfera que frene el movimiento de los cuerpos. El periodo de un satélite artificial que pasase justamente encima de nuestras cabezas sería el mismo que el periodo de las oscilaciones de un cuerpo que viajase por un túnel excavado en la Tierra

$P = 2 π \sqrt{\frac{R^{3}}{G M}} = 5057.96 s = 84.3 min$

Este es el tiempo mínimo que tarda un satélite en completar una vuelta alrededor de la Tierra.

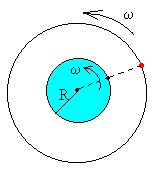Sin embargo, los satélites geoestacionarios dedicados a los comunicaciones tienen un periodo de 24 horas, su velocidad angular es la misma que la de la Tierra y por tanto, permanecen fijos vistos por un observador terrestre.

El radio de un satélite geoestacionario se obtiene poniendo el dato P=24·60·60=86400 s en la fórmula del periodo y despejando r.

$r = \sqrt[3]{\frac{G M P^{2}}{4 π^{2}}} = 42251 \cdot 10^{3} m$

o bien, 35880 km por encima de la superficie de la Tierra.

Actividades

Se introduce

La distancia entre el centro de la Tierra y el túnel horizontal excavado en el interior de la Tierra, actuando en la barra de desplazamiento titulada Posición

Se pulsa el botón titulado Empieza

Se observa el movimiento oscilatorio de una partícula que se introduce por el extremo del túnel, y se comprueba que el periodo de oscilación es de aproximadamente 84 minutos, y es independiente de la posición del túnel.

La amplitud de la oscilación es la mitad de la longitud del túnel.

Ejemplo:

Tomando como unidad de longitud el radio de la Tierra R=6.37·10⁶ m, si el túnel dista del centro de la Tierra y=0.6, la amplitud es

$x = \sqrt{1.0 - {0.6}^{2}} = 0.8$

LineasApplet aparecerá en un explorador compatible JDK 1.1

Referencias

Romer R. The answer is forty-two. Many mechanics problems, only one answer. The Physics Teacher, 41, May 2003, pp. 286-290