• Inicio
• Electromagnetismo
• Campo magnético

Campo magnético producido en un punto fuera del eje de la corriente circular

Vamos a calcular el campo magnético producido por una espira circular en un punto fuera del eje de la espira. La ley de Biot afirma que el campo B producido por una corriente i se obtiene

${\displaystyle B=\frac{{\mu }_{0}i}{4\pi }{\displaystyle \oint \frac{u_t\times u_r}{r^2}}dl}$

Donde dl es un elemento de corriente, u_t es un vector unitario que señala la dirección y sentido de la corriente, y u_r es un vector unitario que señala el punto P donde se calcula el campo magnético.

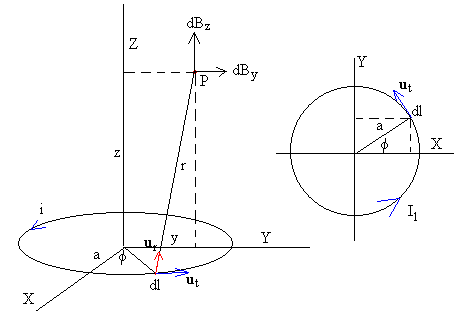
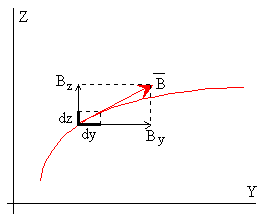
El campo producido por una espira de radio a tiene simetría axial, bastará calcular las componentes B_y y B_z del campo magnético en un punto P (0, y, z) del plano YZ.

Como vemos en la figura la distancia r entre el elemento de corriente dl=a·dø que está situado en el punto (a·cosø , a·senø , 0) y el punto P (0, y, z) considerado es

${\displaystyle \begin{array}{l}r=\sqrt{a^2+y^2+z^2-2ay\sin \phi }\\ u_r=\frac{-a·\cos \phi ·i+(y-a·\sin \phi )·j+z·k}{r}\\ u_t=-\sin \phi ·i+\cos \phi ·j\end{array}}$

Efectuando el producto vectorial u_t × u_r, nos queda las componentes del campo

${\displaystyle \begin{array}{l}{B}_x=\frac{{\mu }_0}{4\pi }i·a·z{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{\cos \phi }{r^3}d\phi }\\ B_y=\frac{{\mu }_0}{4\pi }i·a·z{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{\sin \phi }{r^3}d\phi }\\ B_z=\frac{{\mu }_0}{4\pi }i·a{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{a-y·\sin \phi }{r^3}d\phi }\end{array}}$

La primera integral es inmediata y vale cero B_x=0, ya que para cada elemento de corriente dl existe otro simétrico al plano OYZ cuyo efecto es el de anular la componente X del campo magnético

Las componentes del campo B son

${\displaystyle \begin{array}{l}{B}_y=\frac{{\mu }_0}{2\pi }i·a·z{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}\frac{\sin \phi }{{\left(a^2+z^2+y^2-2ay\sin \phi \right)}^{3/2}}}d\phi \\ B_z=\frac{{\mu }_0}{2\pi }i·a{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}\frac{a-y·\sin \phi }{{\left(a^2+z^2+y^2-2ay\sin \phi \right)}^{3/2}}}d\phi \end{array}}$

Debido a la simetría cilíndrica del problema, solamente tenemos dos componentes del campo  una a lo largo del eje de simetría Z, B_z y la otra en la dirección radial B_y.

Cuando y=0, un punto del eje de la espira, podemos comprobar fácilmente que B_y=0, y que

${\displaystyle B_z=\frac{{\mu }_{0}i}{2}\frac{a^2}{{\left(z^2+a^2\right)}^{3/2}}}$

Para expresar estas integrales en términos de las integrales elípticas completas de primera y segunda especie hacemos el cambio de variable

θ=π/2-ø

${\displaystyle \begin{array}{l}{B}_y=\frac{{\mu }_0}{2\pi }i·a·z{\displaystyle \underset{\pi }{\overset{0}{\int }}\frac{\cos \theta }{{\left(a^2+z^2+y^2-2ay\cos \theta \right)}^{3/2}}}(-d\theta )=-\frac{{\mu }_{0}i}{2\pi }\frac{a}{{(2ay)}^{3/2}}z{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{-\cos \theta ·d\theta }{{(b-\cos \theta )}^{3/2}}}\\ B_z=\frac{{\mu }_0}{2\pi }i·a{\displaystyle \underset{\pi }{\overset{0}{\int }}\frac{a-y·\cos \theta }{{\left(\sqrt{a^2+z^2+y^2-2ay\cos \theta }\right)}^3}}(-d\theta )=\\ \frac{{\mu }_{0}i}{2\pi }\frac{a}{{(2ay)}^{3/2}}\left(a{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\theta }{{(b-\cos \theta )}^{3/2}}}+y{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{-\cos \theta ·d\theta }{{(b-\cos \theta )}^{3/2}}}\right)\\ b=\frac{a^2+z^2+y^2}{2ay}\end{array}}$

Las tablas de integrales elípticas (Good) nos dan las siguientes equivalencias

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\theta }{{(b-\cos \theta )}^{3/2}}}=\frac{m}{2-2m}\sqrt{2m}E(m)E(m)={\displaystyle \underset{0}{\overset{\pi /2}{\int }}\sqrt{1-m{\sin }^2\phi }d\phi }m=\frac{2}{1+b}\\ {\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{-\cos \theta ·d\theta }{{(b-\cos \theta )}^{3/2}}}=\sqrt{2m}K(m)-\frac{2-m}{2-2m}\sqrt{2m}E(m)K(m)={\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\phi }{\sqrt{1-m{\sin }^2\phi }}}\end{array}}$

Las componentes del campo magnético se expresan en términos de las integrales elípticas completas de primera  K(m) y segunda especie E(m) de la siguiente forma.

${\displaystyle \begin{array}{l}{B}_y=\frac{{\mu }_{0}i}{2\pi }\frac{a}{{(2ay)}^{3/2}}z\left(-\sqrt{2m}K(m)+\frac{2-m}{2-2m}\sqrt{2m}E(m)\right)\\ B_z=\frac{{\mu }_{0}i}{2\pi }\frac{a}{{(2ay)}^{3/2}}\left(a\frac{m}{2-2m}\sqrt{2m}E(m)+y\sqrt{2m}K(m)-y\frac{2-m}{2-2m}\sqrt{2m}E(m)\right)\\ m=\frac{2}{1+b}=\frac{4ay}{a^2+z^2+y^2+2ay}\end{array}}$

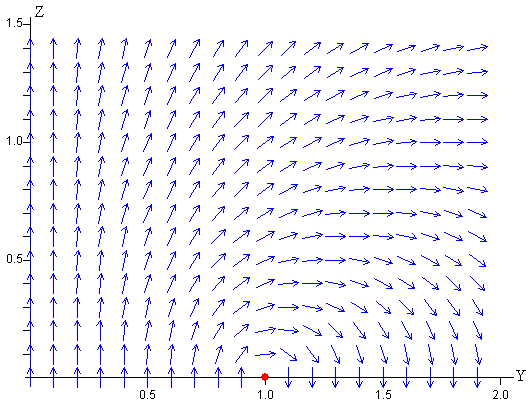
En la figura, se muestra la dirección del campo magnético mediante flechas, en el plano YZ, con y>0  y z>0. El módulo del campo no se puede mostrar ya que cambia significativamente de un punto cercano al anillo a otro algo más alejado. El radio de la espira es a=1.0

Caso particular

Estudiamos el campo a lo largo del eje del anillo, y →0,

${\displaystyle m\to \frac{4ay}{z^2+a^2}}$

las integrales elípticas tienden ambas a K(0)=E(0)=π/2

Como podemos comprobar fácilmente B_y→0, fijarse que los dos términos entre paréntesis se cancelan. En cuanto a la componente Z. Los dos últimos términos ente paréntesis proporcionales a y se cancelan

${\displaystyle B_z\to \frac{{\mu }_{0}i}{2\pi }\frac{a}{{(2ay)}^{3/2}}\left(a\frac{\frac{4ay}{z^2+a^2}}{2}\sqrt{2\frac{4ay}{z^2+a^2}}\frac{\pi }{2}\right)=\frac{{\mu }_{0}i}{2}\frac{a^2}{{(z^2+a^2)}^{3/2}}}$

Resultado que hemos obtenido previamente.

Actividades

Se introduce

• La abscisa (y/a) del punto P, actuando en la barra de desplazamiento titulada Abscisa

• La ordenada (z/a) del punto P, actuando en la barra de desplazamiento titulada Ordenada

Se pulsa en el botón titulado Calcular

El programa interactivo calcula las componentes B_y y B_z del campo, su módulo y el ángulo que forma con el eje Y.

Las componentes del campo B_y y B_z se expresan en términos de (y/a) y (z/a)

${\displaystyle \begin{array}{l}{B}_y=\frac{{\mu }_{0}i}{2a}\frac{1}{\pi {(2(y/a))}^{3/2}}\left(\frac{z}{a}\right)\left(-\sqrt{2m}K(m)+\frac{2-m}{2-2m}\sqrt{2m}E(m)\right)\\ B_z=\frac{{\mu }_{0}i}{2a}\frac{1}{\pi {(2(y/a))}^{3/2}}\left(\frac{m}{2-2m}\sqrt{2m}E(m)+\left(\frac{y}{a}\right)\sqrt{2m}K(m)-\left(\frac{y}{a}\right)\frac{2-m}{2-2m}\sqrt{2m}E(m)\right)\\ m=\frac{2}{1+b}=\frac{4(y/a)}{1+{(z/a)}^2+{(y/a)}^2+2(y/a)}\end{array}}$

El campo en el centro de la espira, z=0, es

${\displaystyle B_z=\frac{{\mu }_{0}i}{2a}}$

El programa interactivo calcula el valor de B_y y de B_z en unidades del campo en el centro de la espira

ForzadasApplet aparecerá en un explorador compatible con JDK 1.1.

Aproximación: Puntos alejados de la espira. Dipolo magnético

Partimos de nuevo de las ecuaciones

${\displaystyle \begin{array}{l}{B}_y=\frac{{\mu }_0}{2\pi }i·a·z{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}\frac{\sin \phi }{{\left(a^2+z^2+y^2-2ay\text{sen}\phi \right)}^{3/2}}}d\phi \\ B_z=\frac{{\mu }_0}{2\pi }i·a{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}\frac{a-y·\sin \phi }{{\left(a^2+z^2+y^2-2ay\sin \phi \right)}^{3/2}}}d\phi \end{array}}$

Si el punto P está lejos de la espira, es decir, si se cumple que

${\displaystyle \sqrt{z^2+y^2}>>a}$

Podemos aproximar el denominador de las dos integrales que nos calculan el campo B_y y B_z.

${\displaystyle {\left(r^2+a^2-2ay\sin \phi \right)}^{-3/2}\approx r^{-3}{\left(1-\frac{2ay·\sin \phi }{r^2}\right)}^{-3/2}\approx r^{-3}\left(1+\frac{3ay·\sin \phi }{r^2}\right)}$

Donde hemos llamado ahora r a

${\displaystyle \begin{array}{l}r=\sqrt{x^2+y^2}\\ B_y\approx \frac{{\mu }_0}{2\pi }i·a·z{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}\frac{1}{r^3}\left(1+\frac{3ay·\sin \phi }{r^2}\right)}\sin \phi ·d\phi =\frac{{\mu }_{0}iaz}{2\pi r^3}{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}\left(\sin \phi +\frac{3ay·{\sin }^{\text{2}}\phi }{r^2}\right)}·d\phi =\\ =\frac{{\mu }_{0}iaz}{2\pi r^3}{\left(-\cos \phi +\frac{3ay}{2r^2}\left(\phi -\frac{1}{2}\sin (2\phi )\right)\right)}_{-\pi /2}^{\pi /2}=\frac{{\mu }_{0}i{a}^2}{4r^3}\left(\frac{3yz}{r^2}\right)\\ B_z\approx \frac{{\mu }_0}{2\pi }i·a{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}(a-y·\sin \phi )\frac{1}{r^3}\left(1+\frac{3ay·\sin \phi }{r^2}\right)}d\phi \\ =\frac{{\mu }_{0}ia}{2\pi r^3}{\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}\left(a-y·\sin \phi -\frac{3a{y}^2·{\sin }^{\text{2}}\phi }{r^2}+\frac{3a^{2}y·\sin \phi }{r^2}\right)}d\phi =\\ \frac{{\mu }_{0}ia}{2\pi r^3}{\left(a\phi -\frac{3a^{2}y·\text{cos}\phi }{r^2}+y·\text{cos}\phi -\frac{3a{y}^2}{2r^2}\left(\phi -\frac{1}{2}\sin (2\phi )\right)\right)}_{-\pi /2}^{\pi /2}=\frac{{\mu }_{0}i{a}^2}{2r^3}\left(1-\frac{3y^2}{2r^2}\right)=\frac{{\mu }_{0}i{a}^2}{4r^3}\left(\frac{3z^2}{r^2}-1\right)\end{array}}$

Las componentes del campo para r>>a, son aproximadamente

${\displaystyle \begin{array}{l}r=\sqrt{x^2+y^2}>>a\\ B_y=\frac{{\mu }_{0}i{a}^2}{4r^3}\left(\frac{3yz}{r^2}\right)\\ B_z=\frac{{\mu }_{0}i{a}^2}{4r^3}\left(\frac{3z^2}{r^2}-1\right)\end{array}}$

El campo creado por una bobina de N espiras apretadas es N veces el campo producido por una de las espiras.

Las dos componentes del campo, B_y y B_z en el punto P (y, z) las podemos expresar en una única fórmula.

${\displaystyle B=\frac{{\mu }_0}{4\pi }\frac{3(m·r)r-r^{2}m}{r^5}}$

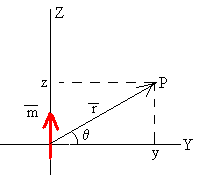
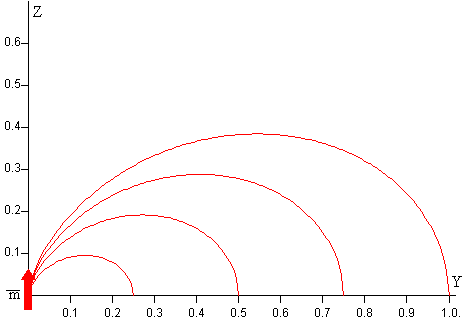
Donde m=i·πa² k es el momento dipolar magnético, señalado mediante una flecha de color rojo.

En el applet se representa las líneas del campo magnético producido por una bobina de pequeño radio a cuyo momento dipolar magnético m se señala mediante una flecha de color rojo.

Líneas de campo magnético

Como el campo es tangente a las líneas de fuerza, la ecuación de las líneas de fuerza es

${\displaystyle \frac{dz}{dy}=\frac{B_z}{B_y}}$

tal como se muestra en la figura.

La ecuación diferencial de las líneas de fuerza para el dipolo magnético es

${\displaystyle \frac{dz}{dy}=\frac{3z^2-r^2}{3yz}=\frac{2z^2-y^2}{3yz}}$

Haciendo el cambio de variable

Z=z², Y=lny

${\displaystyle \frac{dZ}{dY}=\frac{4}{3}Z-\frac{2}{3}\exp (2Y)}$

Para integrar esta ecuación diferencial de primer orden escribimos Z=u·v

${\displaystyle \begin{array}{l}\frac{du}{dY}v+\frac{dv}{dY}u=\frac{4}{3}uv-\frac{2}{3}\exp (2Y)\\ v\left(\frac{du}{dY}-\frac{4}{3}u\right)+\frac{dv}{dY}u=-\frac{2}{3}\exp (2Y)\end{array}}$

Igualamos a cero el paréntesis

${\displaystyle \frac{du}{dY}=\frac{4}{3}u\ln u=\frac{4}{3}Yu=\exp \left(\frac{4}{3}Y\right)}$

La ecuación queda

${\displaystyle \begin{array}{l}\frac{dv}{dY}\exp \left(\frac{4}{3}Y\right)=-\frac{2}{3}\exp (2Y)\\ \frac{dv}{dY}=-\frac{2}{3}\exp \left(\frac{2}{3}Y\right)v=-\exp \left(\frac{2}{3}Y\right)+C\end{array}}$

La solución de la ecuación diferencial es,

${\displaystyle Z=\exp \left(\frac{4}{3}Y\right)\left(-\exp \left(\frac{2}{3}Y\right)+C\right)=C\exp \left(\frac{4}{3}Y\right)-\exp \left(2Y\right)}$

donde C es una constante de integración

Deshaciendo el cambio de variable

${\displaystyle z^2+y^2=C{y}^{4/3}}$

Escribiendo la constante C=D^2/3, D tiene dimensiones de longitud

${\displaystyle {\left(\frac{z}{D}\right)}^2+{\left(\frac{y}{D}\right)}^2={\left(\frac{y}{D}\right)}^{4/3}}$

En la figura, se muestra las líneas del campo magnético para D=0.25, 0.5, 0.75 y 1.0

Referencias

Good R. H. Elliptic integrals, the forgotten functions.Eur. J. Phys. 22 (2001) pp. 119-126.

Mc Tavish J. P., Field pattern of a magnetic dipole. Am. J. Phys. 68 (6) June 2000, pp. 577-57

Fotografía tomada en la VIII Edición del Concurso Ciencia en Acción Zaragoza (2007): Albert Agraz Sánchez, Santiago Clúa. Detector de movimiento por inducción magnética. Universitat de Lleida.

Curso Interactivo de Física en Internet © Ángel Franco García