Agrupación de condensadores. Condensadores ideales en serie

Sean dos condensadores de capacidades C₁ y C₂ dispuestos en serie.

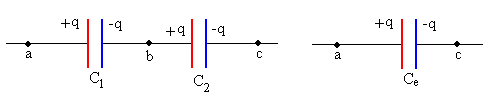
Los dos condensadores tienen la misma carga q. La diferencia de potencial entre a y c es

$V_{a c} = V_{a b} + V_{b c} = \frac{q}{C_{1}} + \frac{q}{C_{1}} = q (\frac{1}{C_{1}} + \frac{1}{C_{2}})$

La agrupación de dos condensadores en serie es equivalente al de un condensador de capacidad C_e

$\frac{1}{C_{e}} = \frac{1}{C_{1}} + \frac{1}{C_{2}}$

Esta es la situación ideal, en la que se supone que los condensadores no pierden carga, las dos placas del condensador están perfectamente aisladas una de la otra. Esto no es lo que ocurre en la situación real.

Condensadores con pérdidas en serie

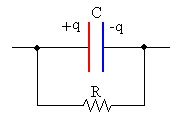Un condensador con pérdida de carga es equivalente a un condensador ideal de capacidad C que se descarga a través de una resistencia R. Como ya hemos estudiado en la página anterior, la carga del condensador disminuye exponencialmente con el tiempo

$q = Q \exp (\frac{- t}{R C})$

La resistencia R no suele ser constante sino que depende de la diferencia de potencial V=q/C entre las placas del condensador. Sin embargo, en nuestro estudio supondremos que la resistencia R es constante. Hay condensadores que tiene constantes de tiempo RC del orden de minutos. Sin embargo, hay otros como aceites o plásticos especiales cuyas constantes de tiempo se miden en horas o en días

Consideremos ahora la situación que se muestra en la figura, en la cual los condensadores tienen pérdidas. Se establece una diferencia de potencial V entre a y c.

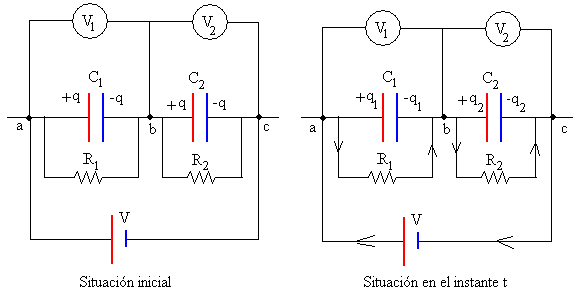
Estado inicial

Inicialmente las cargas de los condensadores son iguales y las diferencias de potencial entre sus placas son respectivamente V₁=q/C₁ y V₂=q/C₂. Por lo que cumple que

$\frac{V_{1}}{V_{2}} = \frac{C_{2}}{C_{1}}$

Como V₁+V₂=V tendremos que

$V_{2} = \frac{V C_{1}}{C_{2} + C_{1}}$

La corriente comienza a fluir a través de las resistencias R₁y R₂ y en general, las cargas en los condensadores serán distintas.

Estado final

Si la diferencia de potencial entre los extremos a y c se mantiene constante, se alcanza un estado estacionario en el que la misma corriente i pasa por las resistencias R₁ y R₂. Se cumplirá entonces que V₁=iR₁ y V₂=iR₂. Por lo que tendremos la relación

$\frac{V_{1}}{V_{2}} = \frac{R_{1}}{R_{2}}$

Como V₁+V₂=V tendremos que

$V_{2} = \frac{V R_{2}}{R_{1} + R_{2}}$

La carga final de cada condensador será q₁=V₁·C₁ y q₂=C₂·V₂, de modo que se cumple la relación

$\frac{q_{1}}{q_{2}} = \frac{C_{1} R_{1}}{C_{2} R_{2}}$

Evolución del estado inicial al final

Supongamos que a los extremos a y c se aplica una diferencia de potencial constante V.

La corriente total i que pasa por a o que sale en b en el instante t, es la suma de dos términos:

la corriente i₁ que pasa por la resistencia R₁ y
la razón del cambio de la carga del condensador con el tiempo dq₁/dt

tal como hemos visto al estudiar el circuito formado por dos condensadores y una resistencia

Del mismo modo, la corriente i que entra en b o que sale en c en el instante t, es la suma de dos términos:

la corriente i₂ que pasa por la resistencia R₂ y
la razón del cambio de la carga del condensador C₂ con el tiempo dq₂/dt

$\frac{d q_{1}}{d t} + i_{1} = \frac{d q_{2}}{d t} + i_{2} C_{1} \frac{d V_{1}}{d t} + \frac{V_{1}}{R_{1}} = C_{2} \frac{d V_{2}}{d t} + \frac{V_{2}}{R_{2}}$

Sustituyendo V₂=V-V₁ tenemos una ecuación en V₂.

$(C_{1} + C_{2}) \frac{d V_{2}}{d t} + (\frac{1}{R_{1}} + \frac{1}{R_{2}}) V_{2} = \frac{V}{R_{1}}$

o bien

$\frac{d V_{2}}{d t} + \frac{1}{T} V_{2} = \frac{V}{R_{1} (C_{1} + C_{2})} T = \frac{R_{2} R_{1} (C_{1} + C_{2})}{R_{1} + R_{2}}$

Integramos esta ecuación diferencial con las siguientes condiciones iniciales: en el instante t=0, la diferencia de potencial entre las placas del condensador C₂ es V₀₂ tal como vimos al principio de este apartado.

$V_{02} = \frac{V C_{1}}{C_{2} + C_{1}}$

Integrando

$\int_{V_{02}}^{V_{2}} \frac{d V_{2}}{\frac{V}{R_{1} (C_{1} + C_{2})} - \frac{1}{T} V_{2}} = \int_{0}^{t} d t$

El resultado final es

$V_{2} (t) = \frac{V}{R_{1} + R_{2}} (R_{2} + \frac{C_{1} R_{1} - C_{2} R_{2}}{C_{1} + C_{2}} \exp (\frac{- t}{T}))$

Comprobación

En el estado inicial t=0 tenemos que

$V_{2} = \frac{V C_{1}}{C_{1} + C_{2}}$

En el estado final t →∞ tenemos

$V_{2} = \frac{V R_{2}}{R_{1} + R_{2}}$

Intensidad de la corriente

La intensidad de la corriente i es igual a

$\begin{array}{l} i = C_{2} \frac{d V_{2}}{d t} + \frac{V_{2}}{R_{2}} \\ i = \frac{V_{0}}{R_{1} + R_{2}} (1 + \frac{{(C_{1} R_{1} - C_{2} R_{2})}^{2}}{R_{1} R_{2} {(C_{1} + C_{2})}^{2}} \exp (\frac{- t}{T})) \end{array}$

La intensidad es máxima en el instante t=0, y tiende hacia un valor constante $\frac{V_{0}}{R_{1} + R_{2}}$ para t→∞

Caso especial

En el caso especial de que C₁R₁=C₂R₂ las diferencias de potencial V₁ y V₂ son independientes del tiempo, aunque la corriente sigue fluyendo a través de cada uno de los condensadores

$\begin{array}{l} V_{2} = \frac{V R_{2}}{R_{1} + R_{2}} V_{1} = \frac{V R_{1}}{R_{1} + R_{2}} \\ q_{2} = \frac{C_{2} R_{2}}{R_{1} + R_{2}} V q_{1} = \frac{C_{1} R_{1}}{R_{1} + R_{2}} V \end{array}$

Como C₁R₁=C₂R₂ las cargas en los condensadores q₁ y q₂ son iguales.

Esta condición se puede cumplir eligiendo adecuadamente la constante dieléctrica k y la resistividad ρ del dieléctrico que se coloca entre las placas de un condensador plano paralelo, cuyas placas tiene un área A y están separadas una distancia d.

La capacidad del condensador es C=kε₀A/d
La resistencia al paso de la corriente es R=ρd/A

El producto de ambas magnitudes solamente depende de la constante dieléctrica k y de la resistividad ρ del dieléctrico, RC=ρ kε₀.

Siempre que de los dieléctricos que separan las placas de los dos condensadores sean tales que cumplan la relación ρ₁ k₁=ρ₂ k₂ se cumplirá también que C₁R₁=C₂R₂

Ejemplo 1:

Los datos del primer condensador son C₁=0.2μF y R₁=5000 MΩ.
Los datos del segundo condensador son C₂=0.5μF y R₂=1000 MΩ.

En el instante inicial t=0 la relación V₁/V₂=2.50. Después de un tiempo suficientemente grande t →∞ V₁/V₂=5.0

Ejemplo 2:

Los datos del primer condensador son C₁=0.1μF y R₁=5000 MΩ.
Los datos del segundo condensador son C₂=0.5μF y R₂=1000 MΩ.

Se cumple el caso especial de que C₁R₁=C₂R₂. La relación V₁/V₂=5 en la situación inicial (t=0) y en la final (t →∞). Aunque la carga de cada condensador no cambia, la intensidad no es nula.

Nota: En el artículo citado en las referencias se obtiene la misma expresión de V₂(t) suponiendo una situación más relista que V pasa de 0 al valor constante V₀ en un tiempo muy corto.

$V (t) = V_{0} (1 - \exp (- t / τ))$

Donde la constante de tiempo τ es muy pequeña comparada con las constantes de tiempo en el proceso de autodescarga de los dos condensadores C₁R₁ ó C₂R₂.

Actividades

Se introduce

la capacidad del primer condensador C₁, en micro Faradios
la resistencia del primer condensador R₁ en mega Ohm
la capacidad del segundo condensador C₂, en micro Faradios
la resistencia del segundo condensador R₂ en mega Ohm
La diferencia de potencial a través de los dos condensadores se mantiene constante e igual a 100 V

Se pulsa el botón titulado Empieza

Se representa en la parte izquierda del applet, V₁/V₂ en función de t/T. Donde T es la constante de tiempo $T = \frac{R_{2} R_{1} (C_{1} + C_{2})}{R_{1} + R_{2}}$

Dos líneas horizontales de color azul, indican el valor inicial del cociente $\frac{V_{1}}{V_{2}} = \frac{C_{2}}{C_{1}}$ en el instante t=0, y el valor final de dicho cociente cuando t →∞ $\frac{V_{1}}{V_{2}} \to \frac{R_{1}}{R_{2}}$

La fuente de alimentación la representamos mediante un depósito muy grande, cuya altura de líquido permanece constante durante toda la "experiencia". Los condensadores con pérdidas los representamos como depósitos de fluido que descargan a través de un capilar:

la anchura del depósito es proporcional a la capacidad C
la altura es proporcional a la diferencia de potencial entre sus placas V
la carga (q=CV) es proporcional al área sombreada de color azul claro.

Observamos como va cambiando la altura de fluido en cada uno de los tubos capilares a medida que transcurre el tiempo. Los puntos de color rojo, representan la intensidad i de la corriente ( movimiento de los portadores de carga positivos) que va disminuyendo con el tiempo, hasta que alcanza el valor constante $\frac{V}{R_{1} + R_{2}}$ cuando t →∞

Nota: En esta página no se demuestra que el circuito eléctrico y el hidráulico representado en el applet tengan un comportamiento análogo. El circuito hidráulico se emplea exclusivamente como imagen para representar los cambios que tienen lugar en el circuito eléctrico a medida que transcurre el tiempo..

LineasApplet aparecerá en un explorador compatible JDK 1.1

Referencias

French A, P. Are the Textbook Writers Wrong about Capacitors?. The Physics Teacher, Vol 31, March 1993, pp156-159