• Inicio
• Electromagnetismo
• Campo eléctrico
• Condensadores

Descarga de un condensador

Consideremos ahora el circuito que consta de un condensador, inicialmente cargado con carga Q, y una resistencia R, y se cierra el interruptor I.

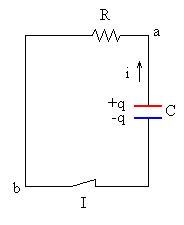La ecuación del circuito será la siguiente.

V_ab+V_ba=0

• Como la corriente va de a hacia b, el potencial de a es más alto que el potencial de b. Por la ley de Ohm V_ab=iR.
• En el condensador la placa positiva a tiene más potencial que la negativa b, de modo que V_ba=-q/C.

La ecuación del circuito es

${\displaystyle iR-\frac{q}{C}=0}$

Como la carga disminuye con el tiempo i=-dq/dt. La ecuación a integrar es

${\displaystyle \begin{array}{l}-R\frac{dq}{dt}=\frac{q}{C}\\ {\displaystyle \underset{Q}{\overset{q}{\int }}\frac{dq}{q}}=-\frac{1}{RC}{\displaystyle \underset{0}{\overset{t}{\int }}dt}q=Q\exp \left(\frac{-t}{RC}\right)\end{array}}$

La carga del condensador disminuye exponencialmente con el tiempo. Derivando con respecto del tiempo, obtenemos la intensidad, en el sentido indicado en la figura.

${\displaystyle i=-\frac{dq}{dt}=\frac{Q}{RC}\exp \left(\frac{-t}{RC}\right)}$

que disminuye exponencialmente con el tiempo.

La descarga tubo-capilar es la analogía hidráulica de la descarga del condensador.

Balance energético

• La energía inicial del condensador es

${\displaystyle E_0=\frac{1}{2}\frac{Q^2}{C}}$

• La energía disipada en la resistencia hasta el instante t es

${\displaystyle E_R={\displaystyle \underset{0}{\overset{t}{\int }}{i}^{2}R·dt}=\frac{Q^2}{2C}\left(1-\exp \left(\frac{-2t}{RC}\right)\right)}$

• La energía almacenada en el condensador en forma de campo eléctrico en el instante t es

${\displaystyle E_c=\frac{1}{2}\frac{q^2}{C}=\frac{Q^2}{2C}\exp \left(\frac{-2t}{RC}\right)}$

Comprobamos que E_c=E₀-E_R. La energía en el condensador se disipa en la resistencia. Cuando se completa el proceso de descarga t→∞, toda la energía almacenada en el condensador se ha disipado en la resistencia

Ejemplo: 

Sea un condensador de capacidad C=1.5 μF en serie con una resistencia de R=58 kΩ cargado inicialmente con Q=45μC. Empecemos a contar el tiempo cuando se cierra el interruptor. En el instante t=60 ms

• La carga del condensador es

${\displaystyle q=45·{10}^{-6}\exp \left(\frac{-60·{10}^{-3}}{58000·1.5·{10}^{-6}}\right)=22.6·{10}^{-6}\text{C}}$

• La intensidad es

${\displaystyle i=\frac{{4510}^{-6}}{58000·1.5·{10}^{-6}}\exp \left(\frac{-60·{10}^{-3}}{58000·1.5·{10}^{-6}}\right)=2.60·{10}^{-4}\text{A}}$

• La energía almacenada inicialmente en el condensador es

${\displaystyle E_0=\frac{1}{2}\frac{{(45·{10}^{-6})}^2}{1.5·{10}^{-6}}=6.75·{10}^{-4}\text{J}}$

• La energía disipada en la resistencia es

${\displaystyle E_R=\frac{{(45·{10}^{-6})}^2}{2·1.5·{10}^{-6}}\left(1-\exp \left(\frac{-2·60·{10}^{-3}}{58000·1.5·{10}^{-6}}\right)\right)=5.05·{10}^{-4}\text{J}}$

• La energía acumulada en el condensador es

${\displaystyle E_C=\frac{1}{2}\frac{{(22.6·{10}^{-6})}^2}{1.5·{10}^{-6}}=1.70·{10}^{-4}\text{J}}$

Actividades

Se introduce

• La capacidad C del condensador, actuando sobre la barra de desplazamiento titulada Condensador
• La resistencia R, actuando sobre la barra de desplazamiento titulada Resistencia
• La carga inicial Q del condensador se ha fijado en el programa

Se pulsa el botón titulado Empieza

Se observa la descarga del condensador, su color pasa gradualmente de rojo (carga positiva) y azul (carga negativa) a blanco (descargado) . A la derecha del applet, se traza la gráfica de la carga q y de la intensidad i en función del tiempo.

Elegir dos valores de la resistencia R₁ y R₂ y dos valores de la capacidad C₁ y C₂ de modo que R₁·C₁=R₂·C₂. Observar como decrece la carga y la intensidad.

LineasApplet aparecerá en un explorador compatible JDK 1.1

Curso Interactivo de Física en Internet © Ángel Franco García