El anillo de Thomson (I)

Corriente inducida en el anillo. Ecuación del circuito

En este apartado, vamos a obtener la intensidad I_a de la corriente inducida en el anillo de forma alternativa.

Considerando de nuevo el anillo como un circuito formado por una resistencia y una autoinducción conectado a una fem alterna. La ecuación del circuito se escribirá: suma de fems igual a intensidad por resistencia

$\begin{array}{l} V_{a} + (- L \frac{d I_{a}}{d t}) = I_{a} \cdot R \\ - M \cdot ω \cdot I_{s 0} \cos (ω t) = L \frac{d I_{a}}{d t} + I_{a} R \end{array}$

La solución de esta ecuación diferencial tiene la siguiente forma

$I_{a} = A \cos (ω t) + B \sin (ω t) + C \exp (- R t / L)$

Los dos primeros términos, corresponden a la solución particular, y el tercer término a la solución homogénea de la ecuación diferencial. El término C se halla a partir de las condiciones iniciales, pero no es necesario calcularlo ya que al cabo de muy poco tiempo la exponencial tiende a cero al ser R>>L. En el estado estacionario, solamente nos queda la solución particular I_a=Acos(ω t)+ Bsen(ω t). Introduciendo la expresión de I_a en la ecuación diferencial obtenemos los valores de A y B.

$I_{a} = - \frac{M \cdot I_{s 0} ω}{R^{2} + ω^{2} L^{2}} (R \cos (ω t) + ω L \sin (ω t))$

Fuerza media sobre el anillo en el estado estacionario.

Como ya se ha explicado, la fuerza sobre el anillo viene dada por la fórmula F_z=-2π a·I_a·B_r.

El campo magnético producido por el solenoide en la posición z que ocupa el anillo de radio a, es proporcional a la corriente I_s que circula por él mismo.

B_r=k(z)·I_s.

Fijado el solenoide, el coeficiente de inducción mutua M del anillo de radio a es función de la posición z del anillo sobre el solenoide.

$\begin{array}{l} F_{z} = - 2 π \cdot a \cdot I_{a} \cdot B_{r} = \frac{2 π a k (z) M (z) \cdot I_{s 0}^{2} ω}{R^{2} + ω^{2} L^{2}} (R \cos (ω t) + ω L \sin (ω t)) \sin (ω t) \\ < F_{z} > = π a k (z) \frac{M (z)}{L} I_{0 s}^{2} (\frac{ω^{2} L^{2}}{R^{2} + ω^{2} L^{2}}) \end{array}$

Vamos a analizar la dependencia de la fuerza media con la intensidad que circula por el solenoide, la frecuencia y la distancia entre el anillo y el solenoide.

Fuerza media <F_z>en función de la intensidad que circula por el solenoide I_s

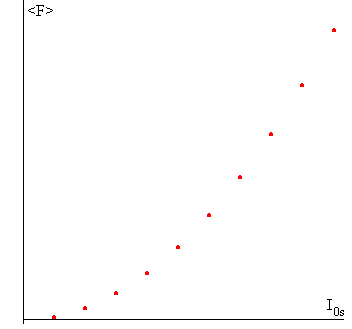El valor medio de la fuerza es proporcional al cuadrado de la amplitud de la intensidad que circula por el solenoide I_0s,

Fuerza media <F_z>en función de la frecuencia ω de la corriente que circula por el solenoide I_s

Para analizar su comportamiento frente a la frecuencia ω,. nos fijaremos en el término entre paréntesis.

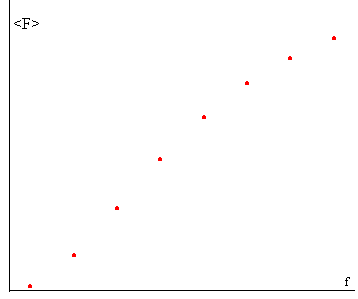$\begin{array}{l} ω < < \frac{R}{L} < F_{z} > \approx π a k \frac{M}{L} I_{0 s}^{2} (ω^{2} \frac{L^{2}}{R^{2}}) \\ ω = \frac{R}{L} < F_{z} > \approx π a k \frac{M}{L} I_{0 s}^{2} (\frac{1}{2}) \\ ω > > \frac{R}{L} < F_{z} > \approx π a k \frac{M}{L} I_{0 s}^{2} (1) \end{array}$

Cuando la frecuencia de la corriente en el solenoide es pequeña frente a R/L la fuerza <F_z> sobre el anillo es proporcional al cuadrado de la frecuencia ω , e inversamente proporcional al cuadrado de la resistencia R.

Cuando la frecuencia ω es mucho más grande que R/L, la fuerza <F_z> sobre el anillo tiende hacia un valor constante, e independiente de la resistencia del anillo.

Fuerza media <F_z>en función de la frecuencia de la distancia z entre el solenoide y el anillo

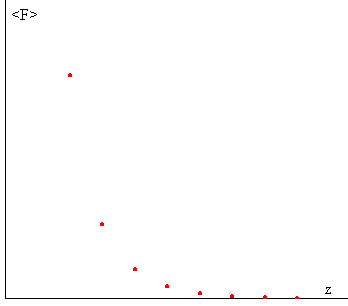La fuerza media <F_z> disminuye rápidamente con la distancia z entre el solenoide y el anillo.

Actividades

En el programa interactivo de esta página, se ha sustituido el solenoide por una bobina, ya que es más sencillo de calcular el campo magnético creado por una bobina, que por un solenoide. El resultado final del "experimento" no cambia desde el punto de vista cualitativo.

Se calcula la fuerza que ejerce una bobina de 100 vueltas sobre un anillo situado a una altura regulable z. Para modificar la distancia z, basta arrastrar con el ratón la flecha horizontal de color azul situada en el borde izquierdo del applet.

Se introduce

La frecuencia f de la corriente que circula por la bobina, en el control de edición titulado Frecuencia.
La amplitud de la intensidad I_s0 que circula por la bobina, en el control de edición titulado Intensidad
La resistencia R del anillo (en unidades 10^-4 Ω), en el control de edición titulado Resistencia
La autoinducción L del anillo (en unidades 10^-7 H), en el control de edición titulado Autoinducción

Se pulsa el botón titulado Inicio para establecer el estado inicial y a continuación, el botón titulado Empieza para dar comienzo a la animación.

A partir de las dimensiones del anillo y del material del que está hecho, podríamos calcular su resistencia y autoinducción. Sin embargo, en el programa interactivo introducimos directamente estas dos magnitudes, para poder ensayar todas las posibilidades, un anillo con o sin resistencia, con o sin autoinducción.

El programa calcula y representa la intensidad de la corriente inducida en el anillo y la fuerza sobre el mismo. Permite por tanto, examinar la fuerza magnética sobre el anillo cambiando los distintos parámetros.

El programa permite visualizar, el movimiento de las cargas (en color rojo) en el solenoide y en el anillo, dándonos una idea del sentido de la corriente inducida. .

En la parte derecha, se representa la corriente en el solenoide (en color azul), en el anillo (en color rojo), y la fuerza sobre el anillo (en color negro) en función del tiempo. Desactivando la casilla titulada intensidades solamente se representa la fuerza sobre el anillo.

Dado que la intensidad de la corriente inducida en el anillo, y la fuerza cambian notablemente a medida que se modifica alguno de los parámetros, se proporciona un control de selección titulado Escalas para modificar la escala vertical de la representación gráfica.

SolenoideApplet aparecerá en un explorador compatible JDK 1.1

Arrastre con el puntero del ratón la flecha de color azul

Experimentos. Representación gráfica

Fuerza sobre el anillo en función de la amplitud de la intensidad I_0s de la corriente en el solenoide

Podemos comprobar, que la fuerza sobre el anillo es proporcional al cuadrado de la intensidad de la corriente que circula en el solenoide.

Frecuencia f=
Distancia z=
Intensidad I_0s	Fuerza media <F> mN
1
2
3
4
5
6
7
8
9
10

Fuerza en función de la frecuencia f de la corriente que circula en el solenoide

La frecuencia con la que se realiza el experimento de laboratorio es de 50 Hz, el programa permite variar la frecuencia en un amplio rango de 10 a 150 Hz. Podremos observar que la fuerza crece rápidamente con la frecuencia, y tiende hacia un valor constante cuando la frecuencia se hace grande.

Intensidad I_0s=
Distancia z=
Frecuencia f	Fuerza media <F> mN
10
30
50
70
90
110
130
150

La fuerza en función de la distancia z entre el anillo y el extremo superior del solenoide.

La inducción mutua M disminuye rápidamente cuando se incrementa z, la distancia entre el solenoide y el anillo. La componente radial del campo magnético producido por el solenoide B_r también disminuye con z. Dado que no podemos proporcionar expresiones simples para la dependencia de estas dos magnitudes con z. El resultado final como podrá comprobar el lector es que la fuerza <F_z> disminuye rápidamente a medida que se incrementa z.

Intensidad I_0s=
Frecuencia f=
Distancia z	Fuerza media <F> mN
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
9.0
10.0

El applet que viene a continuación, nos permite representar los resultados de cada una de las experiencias, y observar la dependencia funcional de la fuerza media sobre el anillo con los tres parámetros que hemos mencionado

Intensidad de la corriente en el solenoide I_s0.
Frecuencia f de la corriente alterna ω =2π f .
Con la distancia z entre el anillo y el solenoide

Por ejemplo, si queremos examinar la dependencia de la fuerza <F_z> con la distancia z entre la bobina y el anillo. Se activa el botón de radio titulado Distancia. Se introduce en los controles de edición del lado izquierdo, bajo la etiqueta X, las distancias z, y en los controles de edición situados en el lado derecho, el valor de <F_z> proporcionado por el programa interactivo previo.

Finalmente, se pulsa en el botón titulado Gráfica.

Se obtendrán representaciones gráficas similares a las de las figuras del apartado titulado Corriente inducida en el anillo.

SolenoideApplet aparecerá en un explorador compatible JDK 1.1

Referencias

Hall J. Forces on the jumping ring. The Physcis Teacher, Vol. 35 February 1997 pp, 80-83.

Tjossem P., Cornejo V. Measurements and mechanisms of Thomson’s jumping ring. Am. J. Phys. 68 (3) March 2000, pp 238-244