Oscilaciones de un émbolo.

Oscilaciones amortiguadas

En la situación estudiada en la página anterior se desprecia el rozamiento en el movimiento del émbolo y se ha supuesto que el gas está en equilibrio en cada instante. Suponiendo que las paredes son perfectamente aislantes, la relación entre la presión y el volumen del gas es de la forma pV^γ=cte. El conjunto formado por el émbolo y el bloque describen una oscilación, que es aproximadamente armónica cuando su la amplitud es pequeña, es decir, cuando el conjunto émbolo-bloque se mueve alrededor de la posición de equilibrio y_e.

Cuando el gas se comprime y se expande rápidamente, con gran turbulencia en el movimiento de sus moléculas, estas no siguen la ley de distribución de Maxwell-Boltzmann. El gas no estará en equilibrio en cada instante, por lo que no existirá una relación definida entre la presión p y el volumen V del gas.

El comportamiento complejo del émbolo que comprime el gas cuando se sitúa un bloque en la posición inicial, se simula mediante el modelo de una oscilación amortiguada.

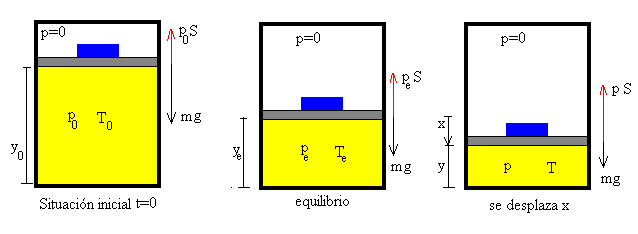
En la figura, se representa la situación inicial, la situación de equilibrio, y cuando el conjunto émbolo-bloque se ha desplazado x=y_e-y de la posición de equilibrio

La ecuación que describe una oscilación amortiguada es

$x = A \cdot \exp (- γ t) \sin (ω t + ϕ) ω = \sqrt{ω_{0}^{2} - γ^{2}}$

Donde ω₀ es la frecuencia de las oscilaciones libres, γ es la constante de amortiguamiento y A y φ son dos constantes que se determinan a partir de las condiciones iniciales.

La velocidad del oscilador en función del tiempo es

$v = \frac{d x}{d t} = A \cdot \exp (- γ t) (ω \cdot cos (ω t + ϕ) - γ \cdot \sin (ω t + ϕ))$

En el instante t=0, la posición del conjunto émbolo-bloque es x₀=y_e-y₀, y su velocidad es v=0. Los valores de la amplitud A y la fase inicial φ son

$A = \frac{x_{0}}{\sin ϕ} \tan ϕ = \frac{ω}{γ}$

La posición y del émbolo en cada instante es y=y_e-x

$y = y_{e} - \frac{y_{e} - y_{0}}{\sin ϕ} \exp (- γ t) \sin (ω t + ϕ)$

Al cabo de un cierto tiempo, teóricamente infinito, la posición final del conjunto bloque-émbolo es y_e, su velocidad final es v=0.

Actividades

Se introduce

El tipo de gas, monoatómico o diatómico, activando el botón de radio correspondiente.
La temperatura inicial T₀ del gas en ºC encerrado en el recipiente, actuando en la barra de desplazamiento titulada Temperatura
La masa del émbolo m₀ se ha fijado en un kg.
El número de moles se ha fijado en n=0.002 mol

Se pulsa el botón titulado Inicio.

Se observa la situación inicial de equilibrio, cuando el émbolo está a una altura y₀.

Se introduce la masa del bloque m_p (en kg), en el control de edición titulado Pesa

Se pulsa el botón titulado Empieza

Se pone el bloque sobre el émbolo y observamos su movimiento

Se representan las fuerzas sobre el conjunto émbolo-bloque,

El peso mg
La fuerza f que ejerce el gas sobre el émbolo debida a la presión

y se proporciona el dato de la resultante f-mg.

Se proporcionan los datos del tiempo y velocidad de émbolo en la parte superior derecha del applet, la temperatura (en kelvin) en la parte inferior del recipiente.

En la parte derecha del applet, se representa la fuerza f que ejerce el gas sobre el émbolo en función de la altura y del émbolo, y se compara con la que corresponde al proceso reversible adiabático. La curva (de color azul) tiene la forma f·y^γ=cte, que es la ecuación de una transformación adiabática. La constante se determina conociendo la fuerza f₀ (presión) y el desplazamiento y₀ (volumen) en el instante t=0.

Finalmente, se representa la energía interna, la energía cinética del conjunto bloque-émbolo y su energía potencial mediante un diagrama en forma de tarta, en el que observamos la transformación de unos tipos de energía en otros.

Ejemplo:

Se introduce

La temperatura 20ºC=293 K
Se selecciona gas monoatómico

Se pulsa el botón titulado Inicio

En el estado inicial de equilibrio, la fuerza que ejerce el gas sobre el émbolo debida a la presión es

f₀=p₀·S= m₀g=1·9.8 N

Conociendo su número n=0.002 de moles y la temperatura T₀=293 K calculamos el volumen o la posición inicial y₀ del émbolo, aplicando la ecuación de los gases perfectos, p₀·V₀=nRT₀

$m_{0} g \cdot y_{0} = n R T_{0} y_{0} = \frac{0.002 \cdot 8.3143 \cdot 293}{1 \cdot 9.8} = 0.497 m = 49 .7 cm$

Se introduce la masa del bloque m_p=3 kg

Se pulsa el botón titulado Empieza.

El émbolo desciende y comprime el gas hasta que se detiene en la posición de equilibrio. El peso del conjunto bloque-émbolo (m₀+m_p)g=mg se iguala a la fuerza f_e que ejerce el gas sobre el émbolo debido a la presión.

f_e=(1+3)·9.8 =39.2 N

Como toda la energía potencial del conjunto bloque-émbolo se convierte en energía interna del gas, la posición final de equilibrio se obtiene

$y_{e} = (\frac{m_{0}}{m} + γ - 1) \frac{y_{0}}{γ} y_{e} = (\frac{1}{4} + \frac{5}{3} - 1) \frac{0.497}{\frac{5}{3}} = 0.273 m$

Calculamos ahora, la temperatura en la nueva situación de equilibrio

$\frac{m \cdot y_{e}}{T_{e}} = \frac{m_{0} y_{0}}{T_{0}} \frac{4 \cdot 0.273}{T_{e}} = \frac{1 \cdot 0.497}{293}$

T_e=644.6 K

Una transformación adiabática entre el estado inicial f₀=m₀g, y₀, y el estado final caracterizado por una fuerza debida a la presión f_e=mg, es

$f_{0} y_{0}^{γ} = f_{e} y_{e}^{γ} y_{e} = {(\frac{1 \cdot 9.8}{4 \cdot 9.8})}^{3 / 5} 0.497 = 0.216 m$

Como vemos en la parte derecha del applet, hay diferencia entre

el proceso descrito en este apartado (en color rojo)
La transformación adiabática (en color azul);