Oscilaciones amortiguadas

En esta página, estudiamos las oscilaciones amortiguadas tomando como modelo una partícula de masa m unida a un muelle elástico de constante k que experimenta una fuerza de rozamiento proporcional a la velocidad. Como aplicación práctica describimos un modelo simplificado que explica la deformación de un balón cuando choca contra una pared rígida.

Oscilaciones amortiguadas

La experiencia nos muestra que la amplitud de un cuerpo vibrante tal como un resorte o un péndulo, decrece gradualmente hasta que se detiene.

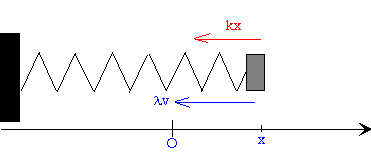
Para explicar el amortiguamiento, podemos suponer que además de la fuerza elástica F=-kx, actúa otra fuerza opuesta a la velocidad F_r=-λv, donde λ es una constante que depende del sistema físico particular. Todo cuerpo que se mueve en el seno de un fluido viscoso en régimen laminar experimenta una fuerza de rozamiento proporcional a la velocidad y de sentido contrario a ésta.

La ecuación del movimiento se escribe

ma=-kx-λv

Expresamos la ecuación del movimiento en forma de ecuación diferencial, teniendo en cuenta que la aceleración es la derivada segunda de la posición x, y la velocidad es la derivada primera de x.

$\frac{d^{2} x}{d t^{2}} + 2 γ \frac{d x}{d t} + ω_{0}^{2} x = 0 ω_{0}^{2} = \frac{k}{m} 2 γ = \frac{λ}{m}$

La solución de la ecuación diferencial tiene la siguiente expresión

$\begin{array}{l} x = A \exp (- γ t) \sin (ω t + ϕ) ω^{2} = ω_{0}^{2} - γ^{2} \\ v = \frac{d x}{d t} = - γ A \exp (- γ t) \sin (ω t + ϕ) + A \exp (- γ t) ω \cos (ω t + ϕ) \end{array}$

La características esenciales de las oscilaciones amortiguadas:

La amplitud de la oscilación disminuye con el tiempo.
La energía del oscilador también disminuye, debido al trabajo de la fuerza F_r de rozamiento viscoso opuesta a la velocidad.
En el espacio de las fases (v-x) el móvil describe una espiral que converge hacia el origen.

Si el amortiguamiento es grande, γ puede ser mayor que ω₀, y ω puede llegar a ser cero (oscilaciones críticas) o imaginario (oscilaciones sobreamortiguadas). En ambos casos, no hay oscilaciones y la partícula se aproxima gradualmente a la posición de equilibrio. La energía que pierde la partícula que experimenta una oscilación amortiguada es absorbida por el medio que la rodea.

Condiciones iniciales

La posición inicial x₀ y la velocidad inicial v₀ determinan la amplitud A y la fase inicial φ . Para t=0,

x₀=A·sinφ
v₀=-Aγ·sinφ+Aω·cosφ

En este sistema de dos ecuaciones se despeja A y φ a partir de los datos de x₀y v₀

$A = \sqrt{x_{0}^{2} + {(\frac{v_{0} + γ x_{0}}{ω})}^{2}} tan ϕ = \frac{x_{0} ω}{v_{0} + γ x_{0}}$

Ejemplo:

Sea una oscilación amortiguada de frecuencia angular propia ω₀=100 rad/s, y cuya constante de amortiguamiento γ=7.0 s^-1. Sabiendo que la partícula parte de la posición x₀=5 con velocidad inicial nula, v₀=0, escribir la ecuación de la oscilación amortiguada.

La frecuencia angular de la oscilación amortiguada ω es

$ω = \sqrt{100^{2} - 7^{2}} = 99.75 rad/s$

5=A·sinφ
0=-7A·sinφ +99.75·A·cosφ

La ecuación de la oscilación amortiguada es

x=5.01·exp(-7t)·sin(99.75t+1.5)

Como vemos la amplitud A no es 5 ni la fase inicial φ es π/2, como en las oscilaciones libres

Posiciones de retorno

Las posiciones de máximo desplazamiento, son aquellas en las que la velocidad del móvil es cero. En la expresión de la velocidad ponemos v=0 y despejamos el argumento ωt+φ

tan(ωt+φ)=ω/γ

$t_{n} = \frac{(\arctan (\frac{ω}{γ}) - ϕ + n π)}{ω} n = 0, 1, 2, ...$

Las posiciones de los puntos de retorno son

$x_{n} = {(- 1)}^{n} A \exp (- γ t_{n}) \sin (\arctan (ω / γ))$

Si el móvil parte de la posición x₀ con velocidad v₀=0, la fase vale tanφ=ω/γ, y A=x₀/sinφ

$t_{n} = \frac{n π}{ω} x_{n} = {(- 1)}^{n} x_{0} \exp (- γ t_{n})$

Ejemplo:

Las sucesivas posiciones de los puntos de retorno para ω₀=100 rad/s, γ=7.0 s^-1 del ejemplo del apartado anterior son:

t₀=0, x₀=5
t₁=0.031, x₁=-4.01
t₂=0.063, x₂=3.22
t₃=0.094, x₃=-2.58

y así, sucesivamente.

La energía del oscilador amortiguado

La energía de la partícula que describe una oscilación amortiguada es la suma de la energía cinética de la partícula y de la energía potencial del muelle elástico deformado.

$E = \frac{1}{2} m v^{2} + \frac{1}{2} k x^{2} = \frac{1}{2} m v^{2} + \frac{1}{2} m ω_{0}^{2} x^{2}$

Introducimos las expresiones de la posición x y de la velocidad v de la partícula en función del tiempo t.

$E = \frac{1}{2} m ω_{0}^{2} A^{2} e^{- 2 γ t} - \frac{1}{2} m γ ω A^{2} e^{- 2 γ t} sin (2 (ω t + ϕ))$

Si la constante de amortiguamiento γ es pequeña, como hemos visto en el ejemplo del apartado anterior ω₀≈ω

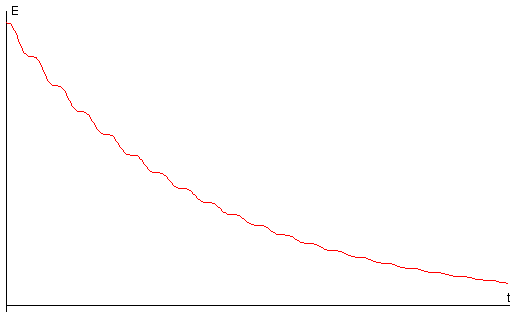
$E = \frac{1}{2} m ω_{0}^{2} A^{2} e^{- 2 γ t} (1 - \frac{γ}{ω_{0}} \sin (2 (ω_{0} t + ϕ)))$

La energía decrece exponencialmente con el tiempo, pero con una pequeña ondulación debida al segundo término entre paréntesis, tal como apreciamos en la figura

Actividades

Se introduce

la posición inicial x₀, en el control de edición titulado Posición
la velocidad inicial del móvil v₀, en el control de edición titulado Velocidad.
la constante de amortiguamiento γ, en el control de edición titulado Cte. amortiguamiento
la frecuencia angular natural del oscilador ω₀ =100 rad/s no se puede modificar

Se pulsa el botón titulado Empieza.

Probar con los siguientes valores de la constante de amortiguamiento γ : 5 (amortiguadas), 100 (críticas), 110 (sobreamortiguadas).

Se observa la posición del móvil en función del tiempo en la parte izquierda de la ventana, gráfico x-t. El valor de la posición x del móvil se muestra en la esquina superior izquierda.
La trayectoria del móvil en el espacio de las fases, gráfico v-x, en la parte superior derecha.
La energía total del móvil en función del tiempo, gráfica E-t, en la parte inferior derecha.

AmortiguadasApplet aparecerá en un explorador compatible con JDK 1.1.