Aproximación al equilibrio de dos gases contenidos en un recinto adiabático y separados por un émbolo.

Modelo cinético de gas ideal

Una vez que se suelta el émbolo situado en la posición x₀, describe varias oscilaciones hasta que alcanza una posición de equilibrio final en el que las presiones a ambos lados del émbolo se igualan. Para determinar los volúmenes finales o las temperaturas finales necesitamos formular un modelo de gas ideal que nos describa la evolución desde el estado inicial al estado final de equilibrio.

El número de moléculas cuya velocidad está comprendida entre v y v+dv, es decir, entre v_x y v_x+dv_x, v_y y v_y+dv_y, v_z y v_z+dv_z, de acuerdo a la ley de Boltzmann es

$d n = N {(\frac{m}{2 π k T})}^{3 / 2} \exp (- \frac{m v^{2}}{2 k T}) d v$

donde dv es un elemento de volumen en el espacio de las velocidades.

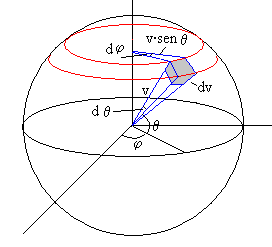Expresamos el elemento de volumen dv en el espacio de velocidades en coordenadas polares. Para ello,

Trazamos dos esferas concéntricas de radio v y v+dv.
Cortamos las esferas por dos planos meridianos que pasan por los ángulos φ y φ+dφ.
Cortamos las esferas por dos planos paralelos de ángulos θ, y θ+dθ

El volumen comprendido es paralepípedo elemental de color gris de la figura tiene por lados

dv
v·sinθ·dφ
v·dθ

Su volumen es

dv=v²·sinθ·dv·dθ·dφ

Número de moléculas del gas que chocan con el émbolo

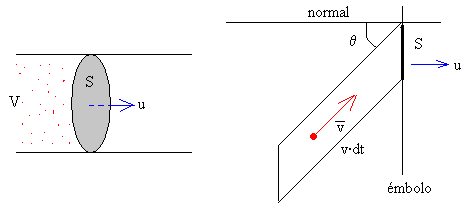
El número de moléculas con velocidad v que chocan contra una porción de émbolo de área S en el tiempo dt, que se mueven en una dirección que hace un ángulo θ con la normal a la pared, son las contenidas en el volumen cilíndrico de base S y altura v·cosθ·dt. Se multiplica el número de moléculas por unidad de volumen (dn/V) por el volumen del cilindro de la figura de la derecha.

(dn/V)·S·v·cosθ·dt.

Ahora bien, el émbolo no está en reposo, sino que se mueve con velocidad u a lo largo de la dirección normal a S. La componente de la velocidad de las moléculas con relación al émbolo es v·cosθ-u. Donde u es positiva cuando el gas incrementa su volumen y negativa cuando lo disminuye. Se supone que u es pequeña comparada con las velocidades moleculares v.

El número de moléculas del gas que chocan con el émbolo en el intervalo de tiempo comprendido entre t y t+dt es

$\frac{1}{V} \int (v \cdot \cos θ - u) \cdot S \cdot d t \cdot d n = \frac{d V}{V} \frac{1}{u} \int (v \cdot \cos θ - u) \cdot d n$

donde dV=S·u·dt es el incremento del volumen del gas

Choque elástico de una molécula con el émbolo

Una partícula de masa m y velocidad v_x choca elásticamente con un émbolo de masa M que se mueve con velocidad u.

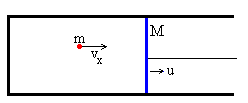
Aplicamos la conservación del momento lineal y la igualdad de la energía cinética antes y después del choque

$\begin{array}{l} m v_{x} + M u = m v_{x}^{'} + M u' \\ \frac{1}{2} m {(v_{x})}^{2} + \frac{1}{2} M u^{2} = \frac{1}{2} m {(v_{x}^{'})}^{2} + \frac{1}{2} M {(u')}^{2} \end{array}$

Escribimos las dos ecuaciones en la forma equivalente

$\begin{array}{l} m (v_{x} - v_{x}^{'}) = M (u' - u) \\ m (v_{x} - v_{x}^{'}) (v_{x} + v_{x}^{'}) = M (u' - u) (u' + u) \end{array}$

Despejando las incógnitas

$\begin{array}{l} v_{x}^{'} = \frac{2 M u + (m - M) v_{x}}{m + M} u' = \frac{2 m v_{x} + (M - m) u}{m + M} \\ v_{x}^{'} = \frac{2 u + (m / M - 1) v_{x}}{m / M + 1} u' = \frac{2 (m / M) v_{x} + (1 - m / M) u}{m / M + 1} \end{array}$

Como la masa M del émbolo es muy grande comparado con masa m de la partícula

$v_{x}^{'} = 2 u - v_{x} u' = u$

Una deducción alternativa es la siguiente:

La partícula choca con el émbolo y cambia el sentido de su velocidad en el Sistema de Referencia del émbolo, la velocidad de la partícula

Antes del choque es (vcosθ-u)
Después del choque es -(vcosθ-u)

En el Sistema de Referencia del Laboratorio, las velocidades de la partícula

Antes del choque es (vcosθ-u)+u= vcosθ
Después del choque es -(vcosθ-u)+u=2u-vcosθ

Variación de la energía interna del gas ideal

El cambio de energía cinética de la partícula es

$Δ E_{k} = \frac{1}{2} m ({(2 u - v \cos θ)}^{2} + v_{y}^{2} + v_{z}^{2}) - \frac{1}{2} m ({(v \cos θ)}^{2} + v_{y}^{2} + v_{z}^{2}) = 2 m u (u - v \cos θ)$

Las moléculas cuando chocan con el émbolo ganan o pierden energía cinética. Si ganan energía cinética, la energía interna del gas aumenta y también lo hace la temperatura y si pierden, la energía interna del gas disminuye.

Vamos a calcular el cambio de energía interna debido a todos los choques de las moléculas del gas con el émbolo móvil en el intervalo de tiempo comprendido entre t y t+dt o bien, cuando el volumen del gas cambia de V a V+dV.

$\begin{array}{l} d U = \frac{d V}{V} \frac{1}{u} \int 2 m u (u - v \cos θ) (v \cdot \cos θ - u) \cdot d n = \\ - 2 m \frac{d V}{V} N {(\frac{m}{2 π k T})}^{3 / 2} \int_{0}^{\infty} \int_{0}^{π / 2} \int_{0}^{2 π} \exp (- \frac{m v^{2}}{2 k T}) {(u - v \cdot \cos θ)}^{2} \cdot v^{2} \sin θ \cdot d v \cdot d θ \cdot d ϕ \end{array}$

Para calcular la integral triple, establecemos los límites de integración para la variable v, φ y θ.

Los límites de la primera integral respecto de φ, son 0 y 2π, se integra para todos los ángulos, pero solamente se integra para ángulos θ comprendidos entre 0 y π/2, ya que cuando θ>π/2, v·cosθ se hace negativa y la partícula se aleja de la pared. Por último, se integra para todas las velocidades, desde 0 a ∞.

$\begin{array}{l} d U = - 4 π m \frac{d V}{V} N {(\frac{m}{2 π k T})}^{3 / 2} \int_{0}^{\infty} \int_{0}^{π / 2} \exp (- \frac{m v^{2}}{2 k T}) (u^{2} v^{2} - 2 u v^{3} \cdot \cos θ + v^{4} \cos^{2} θ) \sin θ \cdot d v \cdot d θ \\ = - 4 π m \frac{d V}{V} N {(\frac{m}{2 π k T})}^{3 / 2} \int_{0}^{\infty} \exp (- \frac{m v^{2}}{2 k T}) (u^{2} v^{2} - u v^{3} + \frac{1}{3} v^{4}) d v \end{array}$

Empleando los resultados de las integrales

$\begin{array}{l} \int_{0}^{\infty} x^{2} \exp (- α x^{2}) = \frac{1}{4} \sqrt{\frac{π}{α^{3}}} \\ \int_{0}^{\infty} x^{3} \exp (- α x^{2}) = \frac{1}{2 α^{2}} \\ \int_{0}^{\infty} x^{4} \exp (- α x^{2}) = \frac{3}{8} \sqrt{\frac{π}{α^{5}}} \end{array}$

Llegamos a la siguiente expresión

$\begin{array}{l} d U = - 4 π m \frac{d V}{V} N {(\frac{m}{2 π k T})}^{3 / 2} {u^{2} \frac{\sqrt{π}}{4} {(\frac{2 k T}{m})}^{3 / 2} - u \frac{1}{2} {(\frac{2 k T}{m})}^{2} + \frac{\sqrt{π}}{8} {(\frac{2 k T}{m})}^{5 / 2}} = \\ - m N \frac{d V}{V} {u^{2} - \frac{2}{\sqrt{π}} u {(\frac{2 k T}{m})}^{1 / 2} + \frac{1}{2} (\frac{2 k T}{m})} \end{array}$

Definimos nuevas variables:

M_g=mN es la masa del gas (m es la masa de una molécula y N es el número de moléculas contenidas en el volumen V del gas). Para un mol de gas, N es el número de Avogadro, N·k=R=8.3143 J/(K·mol)
u=dx/dt es la velocidad del émbolo (x es la posición del émbolo)
V=S·x es el volumen del gas
El cambio infinitesimal de volumen del gas es dV=S·dx=S·(dx/dt)dt
dU=c_v·dT, es la variación de energía interna de un mol de gas ideal. c_v es el calor específico molar a volumen constante.

$c_{v} \frac{d T}{d t} = - \frac{R T}{x} (\frac{d x}{d t}) + \sqrt{\frac{8 R M_{g}}{π}} \frac{\sqrt{T}}{x} {(\frac{d x}{d t})}^{2} - \frac{M_{g}}{x} {(\frac{d x}{d t})}^{3}$

Aproximación al equilibrio

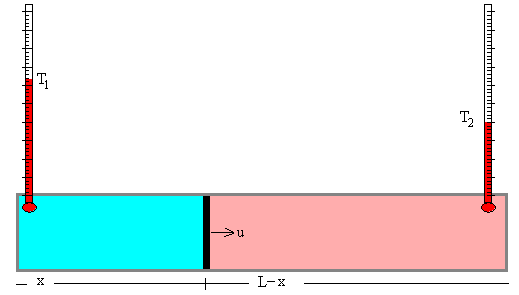
Ahora volvemos al estudio del sistema formado por los dos gases separados por un émbolo móvil

T₁ es la temperatura del gas situado a la izquierda del émbolo
T₂ es la temperatura del gas situado a la derecha del émbolo,
x la posición del émbolo,
S·x es el volumen del gas contenido en la parte izquierda
S·(L-x) el volumen del gas de la parte derecha del émbolo.
Suponemos que el gas de la parte izquierda incrementa su volumen (dx/dt)>0, el gas de la parte derecha disminuye el volumen (dx/dt)<0

Variación de la temperatura

La ecuación para la variación de la temperatura T₁ del gas situado en la parte izquierda es

$c_{v} \frac{d T_{1}}{d t} = - \frac{R T_{1}}{x} (\frac{d x}{d t}) + \sqrt{\frac{8 R M_{g}}{π}} \frac{\sqrt{T_{1}}}{x} {(\frac{d x}{d t})}^{2} - \frac{M_{g}}{x} {(\frac{d x}{d t})}^{3}$

La ecuación para la variación de la temperatura T₂ del gas situado en la parte derecha es

$c_{v} \frac{d T_{2}}{d t} = \frac{R T_{2}}{L - x} (\frac{d x}{d t}) + \sqrt{\frac{8 R M_{g}}{π}} \frac{\sqrt{T_{2}}}{L - x} {(\frac{d x}{d t})}^{2} + \frac{M_{g}}{L - x} {(\frac{d x}{d t})}^{3}$

Aproximación:

Si despreciamos los términos en (dx/dt)² y (dx/dt)³ llegamos a la ecuación

$c_{v} \frac{d T_{1}}{T_{1}} = - R \frac{d x}{x}$

que integrada nos da T₁·x^γ^-1=cte

De modo similar, obtenemos T₂(L-x)^γ^-1=cte

Recuérdese que c_p=c_v+R y γ=c_p/c_v

Ecuación del movimiento del émbolo

Como el sistema es aislado, la energía total permanece constante

$\frac{1}{2} M {(\frac{d x}{d t})}^{2} + c_{v} T_{1} + c_{v} T_{2} = cte$

El primer término es la energía cinética del émbolo de masa M. El segundo, la energía interna de un mol de gas contenido en la parte izquierda y el tercero, la energía interna de un mol de gas contenido en la parte derecha.

Derivamos con respecto del tiempo

$M (\frac{d x}{d t}) (\frac{d^{2} x}{d t^{2}}) + c_{v} \frac{d T_{1}}{d t} + c_{v} \frac{d T_{2}}{d t} = 0$

Despejamos la aceleración d²x/dt²

$\frac{d^{2} x}{d t^{2}} = \frac{R}{M} (\frac{T_{1}}{x} - \frac{T_{2}}{L - x}) - \frac{1}{M} \sqrt{\frac{8 R M_{g}}{π}} (\frac{\sqrt{T_{1}}}{x} + \frac{\sqrt{T_{2}}}{L - x}) (\frac{d x}{d t}) + \frac{M_{g}}{M} (\frac{1}{x} - \frac{1}{L - x}) {(\frac{d x}{d t})}^{2}$

Aproximación

Si despreciamos los términos en (dx/dt)² y (dx/dt)³ el émbolo describe un movimiento periódico.

$\begin{array}{l} M \frac{d^{2} x}{d t^{2}} = R (\frac{T_{1}}{x} - \frac{T_{2}}{L - x}) \\ M \frac{d^{2} x}{d t^{2}} = R (\frac{T_{10} x_{0}^{γ - 1}}{x^{γ}} - \frac{T_{20} {(L - x_{0})}^{γ - 1}}{{(L - x)}^{γ}}) \end{array}$

que estudiamos en el primer apartado, oscilaciones del émbolo

En el caso general, se resuelve el sistema de dos ecuaciones diferenciales de primer orden y una ecuación de segundo orden con las condiciones iniciales siguientes: en el instante t=0,

La posición del émbolo es x₀, su velocidad inicial es cero dx/dt=0
La temperatura inicial del gas situado en la parte izquierda es T₁₀
La temperatura inicial del gas situado en la parte derecha es T₂₀

En el estado final de equilibrio dx/dt=0, y d²x/dt²=0

$\frac{T_{1 f}}{x_{f}} - \frac{T_{2 f}}{L - x_{f}} = 0$

que corresponde a la igualdad de presiones p_1f=p_2f=p_f a un lado y otro del émbolo, tal como hemos visto en la introducción

Escalas

Antes de resolver numéricamente el sistema de tres ecuaciones diferenciales, es conveniente escribirlas en términos de las siguientes variables adimensionales

$\begin{array}{l} θ_{1} = \frac{T_{1}}{T_{10} + T_{20}} θ_{2} = \frac{T_{2}}{T_{10} + T_{20}} γ = \frac{c_{p}}{c_{v}} c_{p} = c_{v} + R \\ ξ = \frac{x}{L} τ = \frac{t}{\sqrt{\frac{M L^{2}}{R (T_{10} + T_{20})}}} δ = \sqrt{\frac{8 M_{g}}{π M}} \end{array}$

Las ecuaciones diferenciales se convierten en

$\begin{array}{l} \frac{d θ_{1}}{d τ} = - (γ - 1) \frac{θ_{1}}{ξ} \frac{d ξ}{d τ} + δ (γ - 1) \frac{\sqrt{θ_{1}}}{ξ} {(\frac{d ξ}{d τ})}^{2} - \frac{π}{8} (γ - 1) δ^{2} \frac{1}{ξ} {(\frac{d ξ}{d τ})}^{3} \\ \frac{d θ_{2}}{d τ} = (γ - 1) \frac{θ_{2}}{1 - ξ} \frac{d ξ}{d τ} + δ (γ - 1) \frac{\sqrt{θ_{2}}}{1 - ξ} {(\frac{d ξ}{d τ})}^{2} + \frac{π}{8} (γ - 1) δ^{2} \frac{1}{1 - ξ} {(\frac{d ξ}{d τ})}^{3} \\ \frac{d^{2} ξ}{d τ^{2}} = \frac{θ_{1}}{ξ} - \frac{θ_{2}}{1 - ξ} - δ (\frac{\sqrt{θ_{1}}}{ξ} + \frac{\sqrt{θ_{2}}}{1 - ξ}) \frac{d ξ}{d τ} + \frac{π}{8} δ^{2} (\frac{1}{ξ} - \frac{1}{1 - ξ}) {(\frac{d ξ}{d τ})}^{2} \end{array}$

Se resuelve el sistema de ecuaciones diferencias por procedimientos numéricos, con las siguientes condiciones iniciales, en el instante τ=0, ξ=ξ₀, (dξ/dτ)₀=0,θ₁=θ₁₀, θ₂=1-θ₁₀

Se comprueba que se cumple la conservación de la energía expresada en términos de las variables adimensionales de la forma

$\frac{1}{2} (γ - 1) {(\frac{d ξ}{d τ})}^{2} + θ_{1} + θ_{2} = 1$

En el estado final, (dξ/dτ)=0 y (d²ξ/dτ²)=0 la relación entrelas variables adimensionales serán:

Conservación de la energía

θ_1f+θ_2f=1

En la ecuación del movimiento del émbolo

$\frac{θ_{1 f}}{ξ_{f}} = \frac{θ_{2 f}}{1 - ξ_{f}}$

Equivalente a la igualdad de presiones a uno y otro lado del émbolo

Concluyendo: el modelo cinético de gas ideal nos predice los valores finales de equilibrio de las temperaturas T_1f, T_2f y de los volúmenes V_1f=S·x_f_,V_2f=S·(L-x_f), mientras que la Termodinámica solamente nos dice que las presiones de los gases se deberán de igualar.

Actividades

Se pulsa el botón titulado Inicio

Se introduce

La temperatura adimensional inicial θ₁₀ del gas situado en la parte izquierda del cilindro, actuando en la barra de desplazamiento titulada Temperatura 1
La temperatura inicial del gas situado en la parte derecha del cilindro vale θ₂₀=1-θ₁₀
El valor del parámetro δ, en el control de edición titulado Parámetro

Se pulsa el botón titulado Empieza

Observamos las oscilaciones del émbolo, hasta que al cabo de cierto tiempo alcanza la posición de equilibrio. Cuanto mayor sea el valor del parámetro δ, antes se alcanzará dicha posición.

Los termómetros marcan en cada instante las temperaturas adimensionales θ₁ y θ₂

En la parte superior del applet, se representa la posición ξ del émbolo en función del tiempo adimensional τ.

En la parte superior derecha del applet, se representa un diagrama en forma de tarta:

en color azul, la energía interna del gas situado en la parte izquierda del cilindro, θ₁
en color rojo, la energía interna del gas situado en la parte derecha, θ₂
en color negro, la energía cinética del émbolo en términos de variables adimensionales

Probar los siguientes ejemplos:

θ₁₀=0.9, ξ₀=0.1,δ=0.1
θ₁₀=0.7, ξ₀=0.4,δ=0.0
θ₁₀=0.9, ξ₀=0.1,δ=0.05

Mueva el émbolo con el puntero del ratón

Referencias

Crosignani B., Di Porto P., Approach to thermal equilibrium in a system with adiabatic constraints. Am. J. Phys. 64 (5) May 1996, pp. 610-613

Bauman R. O., Cockerham III H. L. Pressure of an ideal gas on a moving piston. Am. J. Phys. 37 (7) July 1969, pp. 675-679