Deducción de la ecuación de la transformación adiabática a partir de un modelo simple de gas ideal

En esta página, vamos a deducir la ecuación de una transformación adiabática mediante dos modelos consistentes en un gas ideal contenido en un cilindro cerrado con un émbolo móvil.

El primer modelo, es similar al estudiado en la la página anterior,
El segundo, es es un gas ideal que consta de una sola partícula

Un gas ideal contenido en un cilindro con un émbolo móvil

En la deducción de la ley de los gases ideales a partir de los choques de las moléculas con las paredes del recipiente, hemos supuesto que el émbolo está fijo. De modo, que la molécula rebota cuando choca con el émbolo cambiando el signo de la componente X su velocidad.

Mediante un modelo simple, se han interpretado microscópicamente las magnitudes macroscópicas presión y temperatura. Los pasos han sido los siguientes:

Se determina el cambio de momento lineal que experimenta una molécula cuando choca con el émbolo.
Se determina el número de choques que experimentan las moléculas con el émbolo en la unidad de tiempo.
Se calcula la fuerza que ejerce el émbolo sobre las moléculas del gas para producirles dicho cambio de momento lineal.
Se relaciona la temperatura con la energía cinética media de las moléculas.

En la derivación de la ecuación de la transformación adiabática, no se emplea ni el primer principio ni la ecuación de estado de un gas ideal, solamente la relación entre energía cinética media de las moléculas del gas y su temperatura, es decir, la definición cinética de temperatura.

Choque de una molécula contra un émbolo móvil

Cuando un émbolo se mueve hacia la izquierda comprimiendo el gas encerrado en el recipiente, las moléculas que chocan contra el émbolo, como podemos ver en las sucesivas figuras, incrementan su velocidad a causa de su choque con una pared móvil.

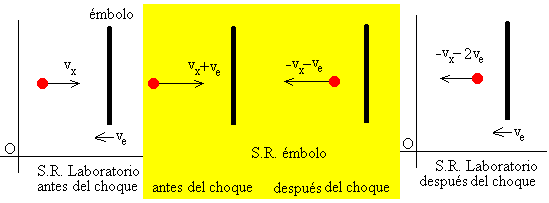
cinetica1.gif (4993 bytes)

Cada molécula del gas cambia su velocidad en el choque contra el émbolo móvil desde v_x a –v_x-2v_e.

Se supone que el émbolo no cambia de velocidad como resultado del choque con las moléculas ya que su masa M es muy grande comparada con la masa m de una molécula.

Deducción alternativa

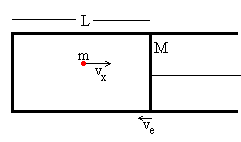
cinetica.gif (1613 bytes)

Una partícula de masa m y velocidad v_x choca elásticamente con un émbolo de masa M que se mueve con velocidad (–v_e).

Conservación del momento lineal y la igualdad de la energía cinética antes y después del choque

$\begin{array}{l} m v_{x} + M (- v_{e}) = m v_{x}^{'} + M v_{e}^{'} \\ \frac{1}{2} m {(v_{x})}^{2} + \frac{1}{2} M {(v_{e})}^{2} = \frac{1}{2} m {(v_{x}^{'})}^{2} + \frac{1}{2} M {(v_{e}^{'})}^{2} \end{array}$

Escribimos las dos ecuaciones en la forma equivalente

$\begin{array}{l} m (v_{x} - v_{x}^{'}) = M (v_{e}^{'} + v_{e}) \\ m (v_{x} - v_{x}^{'}) (v_{x} + v_{x}^{'}) = M (v_{e}^{'} + v_{e}) (v_{e}^{'} - v_{e}) \end{array}$

Despejando las incógnitas

$\begin{array}{l} v_{x}^{'} = \frac{- 2 M v_{e} + (m - M) v_{x}}{m + M} v_{e}^{'} = \frac{2 m v_{x} - (M - m) v_{e}}{m + M} \\ v_{x}^{'} = \frac{- 2 v_{e} + (m / M - 1) v_{x}}{m / M + 1} v_{e}^{'} = \frac{2 (m / M) v_{x} - (1 - m / M) v_{e}}{m / M + 1} \end{array}$

Como la masa M del émbolo es muy grande comparado con masa m de la partícula

$v_{x}^{'} = - 2 v_{e} - v_{x} v_{e}^{'} = v_{e}$

El émbolo no cambia de velocidad como resultado del choque con las moléculas ya que su masa M es muy grande comparada con la masa m de una molécula. Sin embargo, como el número de choques es muy grande, para que el émbolo se mantenga con velocidad constante es necesario ejercer una fuerza.

Mediante este mecanismo, el émbolo incrementa la energía de las partículas encerradas en el recipiente. La velocidad de desplazamiento del émbolo es muy pequeña comparada con la velocidad de las moléculas, la energía ganada por una molécula en su choque con el émbolo es rápidamente redistribuida entre las otras moléculas del gas, de modo que el gas está siempre en equilibrio.

Supongamos que el gas consiste en N partículas contenidas en el volumen cilíndrico de longitud L, tal como se muestra en la figura.

Si el gas tiene N partículas, el tiempo medio entre dos colisiones es

$Δ t = \frac{2 L}{N v_{x}}$

La ganancia de energía cinética que experimenta el gas en cada choque con el émbolo es

$\frac{1}{2} m {(- v_{x} - 2 v_{e})}^{2} - \frac{1}{2} m v_{x}^{2} = 2 m v_{x} v_{e} (1 + \frac{v_{e}}{2 v_{x}}) \approx 2 m v_{x} v_{e}$

Hemos supuesto que la velocidad con la que se mueve el émbolo v_e es mucho más pequeña que la velocidad promedio v_x de las moléculas del gas.

Incremento de la temperatura del gas durante la compresión

El incremento de energía cinética en cada choque se redistribuye entre todas las moléculas del gas. La energía media ganada por partícula es $2 m v_{x} v_{e} / N$ y este incremento de energía se refleja en un incremento de temperatura

$\frac{3}{2} k Δ T = \frac{2 m v_{x} v_{e}}{N}$

donde la velocidad de desplazamiento del émbolo es v_e=-ΔL/Δt, el desplazamiento ΔL del émbolo que ocurre entre dos choques sucesivos Δt.

Introducimos el valor de Δt (tiempo medio entre dos colisiones) calculado en el apartado anterior.

$\frac{3}{2} k Δ T = - m v_{x}^{2} \frac{Δ L}{L}$

Como hemos visto en la página anterior, las velocidades a lo largo del eje X no estarán relacionadas con las velocidades a lo largo del eje Y o Z, por tanto, < v²>=3< v²_x>.

$\frac{3}{2} k Δ T = - m \frac{v^{2}}{3} \frac{Δ L}{L}$

Como el término mv² es el doble de la energía cinética media, expresándolo en función de la temperatura T, queda la relación

$\frac{3}{2} k Δ T = - k T \frac{Δ L}{L}$

Finalmente, la relación entre las magnitudes macroscópicas volumen y temperatura es,

$\frac{Δ T}{T} = - \frac{2}{3} \frac{Δ V}{V}$

Integrando obtenemos la relación entre el volumen y la temperatura del gas ideal o bien, la relación entre la presión y el volumen

$T V^{2 / 3} = cte P V^{5 / 3} = cte$

Para un gas monoatómico, los calores específicos son: c_v=3R/2 y c_p=c_v+R=5R/2. De modo que γ =c_p/c_v=5/3

La ecuación para una transformación adiabática es por tanto,

$p V^{γ} = cte$