• Inicio
• Fluidos
• Estática
• Principio de Arquímedes

Oscilaciones de una esfera que flota en el agua

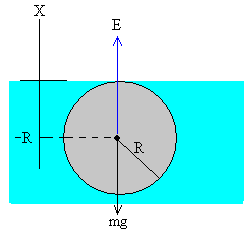Consideremos una esfera de radio R que tiene una densidad ρ<1 y que se mantiene completamente sumergida en agua. Se suelta la esfera y se observa su movimiento oscilatorio En esta página, vamos a comprobar que su comportamiento difiere del Movimiento Armónico Simple (M.A.S.).

Ecuación del movimiento

Supondremos que el agua y el aire son fluidos ideales, que no ejercen fuerzas de rozamiento sobre la esfera en movimiento.

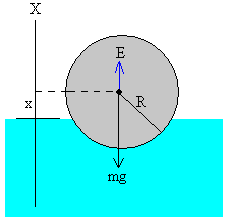
Para describir el movimiento, situamos el origen del eje X en la superficie del agua y llamamos x a la posición del centro de la esfera

• Cuando x=-R, la esfera se encuentra completamente sumergida

• Cuando x=+R la esfera se encuentra justamente fuera del agua

Cuando la esfera se encuentra parcialmente sumergida las fuerzas que actúan son:

• El peso mg

• El empuje E

 Para una esfera de densidad ρ relativa al agua (cuya densidad es la unidad) la masa es

${\displaystyle m=\rho \frac{4}{3}\pi R^3}$

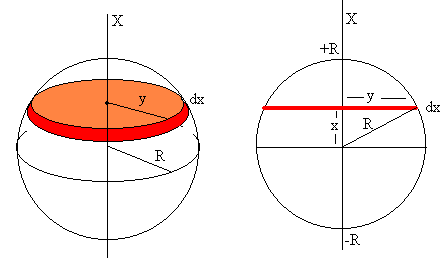
El empuje es el peso en agua del volumen de la parte sumergida. Calculamos el volumen de la parte de la esfera sumergida en agua. Este volumen V es la suma (integral) de los elementos diferenciales de volumen de radio y y de altura dx, uno de los cuales se muestra en la figura.

${\displaystyle V={\displaystyle \underset{x}{\overset{R}{\int }}\pi y^{2}dx}={\displaystyle \underset{x}{\overset{R}{\int }}\pi (R^2-x^2)dx}=\frac{\pi R^3}{3}\left(2-3\frac{x}{R}+\frac{x^3}{R^3}\right)}$

Cuando x=-R obtenemos el volumen de la esfera 4πR³/3

La ecuación del movimiento es

${\displaystyle m\frac{d^{2}x}{d{t}^2}=E-mg\frac{d^{2}x}{d{t}^2}=g\left(\frac{1}{4\rho }\left(2-3\frac{x}{R}-\frac{x^3}{R^3}\right)-1\right)}$

Para calcular la posición x del centro de la esfera en función del tiempo t, resolvemos esta ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales, en el instante t=0, x=-R, dx/dt=0. Cuando la esfera se encuentra completamente sumergida x=-R se suelta (su velocidad inicial es cero)

Transformamos la ecuación diferencial de segundo orden, en la ecuación diferencial de primer orden

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=\frac{dv}{dt}=\frac{dv}{dx}\frac{dx}{dt}=v\frac{dv}{dx}\\ v\frac{dv}{dx}=g\left(\frac{1}{4\rho }\left(2-3\frac{x}{R}-\frac{x^3}{R^3}\right)-1\right)\end{array}}$

Que podemos integrar entre x=-R donde la velocidad de la esfera es nula (posición inicial)  y la posición x≤R, donde la velocidad es v.

${\displaystyle v^2=2gR\left(-1-\frac{x}{R}+\frac{1}{16\rho }\left(13+8\frac{x}{R}-6\frac{x^2}{R^2}+\frac{x^4}{R^4}\right)\right)}$

Cuando x=R la esfera se encuentra completamente fuera del agua y su velocidad es

${\displaystyle v_1^2=2gR\left(\frac{1-2\rho }{\rho }\right)}$

a partir de este momento se eleva en el aire hasta una altura máxima y vuelve a caer en el agua, volviendo a sumergirse hasta alcanzar la posición inicial de partida, repitiéndose de nuevo la oscilación.

La esfera sale completamente fuera del agua en el caso de que su densidad sea ρ<0.5. Si la densidad es mayor que esta cantidad, la esfera permanece parcialmente sumergida durante su movimiento oscilatorio.

• Cuando la densidad relativa de la esfera es ρ<0.5.

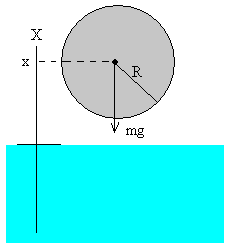A partir de la posición x=R, la esfera sale completamente fuera del agua y sobre la esfera solamente actúa la fuerza constante peso. Las ecuaciones del movimiento son

${\displaystyle \begin{array}{l}v=v_1+(-g)(t-t_1)\\ x=R+v_1·(t-t_1)+\frac{1}{2}(-g){\left(t-t_1\right)}^2\end{array}}$

Siendo t₁ el instante en el que el centro de la esfera pasa por la posición x=R.

Alternativamente, aplicando el principio de conservación de la energía

${\displaystyle \begin{array}{l}\frac{1}{2}m{v}^2+mgx=\frac{1}{2}m{v}_1^2+mgR\\ v^2=v_1^2-2g(x-R)\end{array}}$

El centro de la esfera se eleva hasta la altura máxima cuando v=0.

${\displaystyle x_{máx}=R\left(\frac{1-\rho }{\rho }\right)}$

Por ejemplo:

• Densidad ρ=0.4

• El radio de la esfera R=1

 La esfera parte de la posición x=-1 con velocidad v=0, y llega a la posición x=+1 con una velocidad v₁.

${\displaystyle v_1^2=2·9.8\left(\frac{1-2·0.4}{0.4}\right)v_1=\sqrt{9.8}\text{m/s}}$

Asciende en el aire hasta que el centro de la esfera alcanza la altura máxima

${\displaystyle x=1+\frac{v_1^2}{2·9.8}=1.5\text{m}}$

• Cuando la esfera tiene una densidad relativa ρ>0.5.

La velocidad de de su centro es cero cuando

${\displaystyle \frac{x^4}{R^4}-6\frac{x^2}{R^2}+(8-16\rho )\frac{x}{R}+(13-16\rho )=0}$

Una de las raíces de esta ecuación es x/R=-1, ya que la esfera parte del reposo cuando x=-R.

${\displaystyle \left(\frac{x}{R}+1\right)\left(\frac{x^3}{R^3}-\frac{x^2}{R^2}-5\frac{x}{R}+13-16\rho \right)=0}$

Tenemos que resolver la ecuación cúbica

x³+ax²+bx+c=0

a=-R, b=-5R², c=(13-16ρ)R³

 Se calcula los parámetros

${\displaystyle \begin{array}{l}Q=\frac{a^2-3b}{9}=\frac{16}{9}{R}^2\\ S=\frac{2a^3-9ab+27c}{54}=\frac{152-216\rho }{27}{R}^3\end{array}}$

Si S²<Q³ entonces la ecuación tiene tres raíces reales. Esta desigualdad equivale a

729ρ²-1026ρ+297<0        que se cumple para ρ<1

Las tres raíces reales se calculan según las fórmulas

${\displaystyle \begin{array}{l}\theta =\arccos \left(\frac{S}{\sqrt{Q^3}}\right)\\ x_1=-2\sqrt{Q}\cos \left(\frac{\theta }{3}\right)-\frac{a}{3}\\ x_2=-2\sqrt{Q}\cos \left(\frac{\theta +2\pi }{3}\right)-\frac{a}{3}\\ x_3=-2\sqrt{Q}\cos \left(\frac{\theta -2\pi }{3}\right)-\frac{a}{3}\end{array}}$

Por ejemplo, para ρ=0.7, las raíces son x₁=-1.98·R, x₂=2.64·R, x₃=0.34·R.  La última es la que corresponde a v=0.

Cuando ρ=13/16=0.8125, la velocidad de la esfera v=0 se hace cero cuando x=0.

• Cuando la esfera tiene una densidad relativa ρ=0.5.

La velocidad del centro de la esfera tiene es

${\displaystyle v^2=\frac{gR}{4}\left(5-6u^2+u^4\right)u=\frac{x}{R}}$

que se hace cero cuando x=R

El periodo o tiempo que tarda en efectuar una oscilación completa es

${\displaystyle P=2{\displaystyle \underset{-R}{\overset{+R}{\int }}\frac{dx}{v}=}4\sqrt{\frac{R}{g}}{\displaystyle \underset{-1}{\overset{+1}{\int }}\frac{du}{\sqrt{5-6u^2+u^4}}=}8\sqrt{\frac{R}{g}}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{du}{\sqrt{5-6u^2+u^4}}}}$

Haciendo el cambio de variable u=senφ, el periodo P se expresa mediante una integral elíptica completa de primera especie

${\displaystyle P=\frac{8}{\sqrt{5}}\sqrt{\frac{R}{g}}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{\text{d}\varphi }{\sqrt{1-\frac{1}{5}{\sin }^2\varphi }}}=\frac{8}{\sqrt{5}}·1.6596\sqrt{\frac{R}{g}}=5.9376\sqrt{\frac{R}{g}}}$

En la página titulada Movimiento sobre una superficie semicircular cóncava hay un programa interactivo que calcula la integral elíptica completa. En este caso, hemos de introducir el control de edición el ángulo θ₀ en grados, tal que

${\displaystyle \text{sin}\frac{{\theta }_0}{2}=\frac{1}{\sqrt{5}}{\theta }_0=53.13º}$   

Ejemplo

• Densidad ρ=0.5

• El radio de la esfera R=1

El periodo de una oscilación completa es

${\displaystyle P=5.9376\sqrt{\frac{1.0}{9.8}}=1.90\text{s}}$

Actividades

Se introduce

• La densidad relativa ρ de la esfera, actuando en la barra de desplazamiento titulada Densidad relativa

• El radio de la esfera se ha fijado en R=1

Se pulsa el botón titulado Empieza

En la parte izquierda del applet, observamos el movimiento de la esfera

En la parte derecha del applet, se representa su comportamiento en el espacio de las fases

• En el eje vertical se representa la velocidad en unidades $w=\frac{v}{\sqrt{2gR}}$  

• En el eje horizontal, los desplazamientos en unidades del radio de la esfera u=x/R

FluidoApplet1 aparecerá en un explorador compatible con JDK 1.1.

Referencias

Lapidus I. R. Problem: oscillating buoyant sphere.  Am. J. Phys. 54 (9) September 1986. Enunciado en pág 831, Solución en pág. 849

Curso Interactivo de Física en Internet © Ángel Franco García