Movimiento sobre una superficie semicircular cóncava

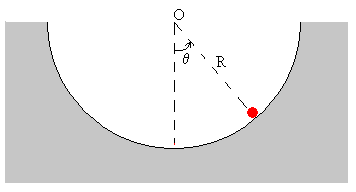
En esta página, se estudia el movimiento de una partícula que desliza sobre una superficie semicircular cóncava de radio R.

Este ejemplo, nos sugiere una posible práctica de laboratorio para la medida del coeficiente de rozamiento cinético.

Movimiento sin rozamiento

Las fuerzas sobre la partícula:

El peso, mg
La reacción de la superficie circular sobre la que desliza, N

La ecuación del movimiento a lo largo de la dirección radial es

$N - m g \cos θ = m a_{n} a_{n} = \frac{v^{2}}{R}$

La ecuación del movimiento a lo largo de la dirección tangencial es

$m a_{t} = - m g \sin θ R \frac{d^{2} θ}{d t^{2}} = - g \sin θ$

que se resuelve por procedimientos numéricos con las condiciones iniciales t=0, θ= -θ₀, dθ/dt=0.

Principio de conservación de la energía

A medida que la partícula desliza por la superficie semicircular, va aumentando su velocidad. La energía potencial se va transformando en energía cinética.

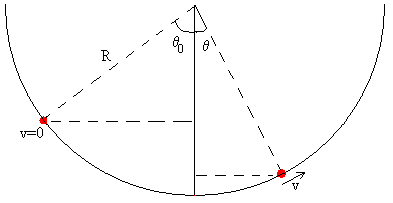
Si la partícula parte de la posición angular –θ₀ con velocidad inicial cero. Aplicamos el principio de conservación de la energía para calcular la velocidad v de la partícula cuando se encuentra en la posición θ

$- m g R \cos θ_{0} = \frac{1}{2} m v^{2} - m g R \cos θ$

Como v=Rdθ/dt, obtenemos la ecuación diferencial de primer orden.

$\frac{d θ}{d t} = \sqrt{2 \frac{g}{R} (\cos θ - \cos θ_{0})}$

Obtenemos una expresión similar cuando determinamos el tiempo que tarda en caer la varilla inclinada, y el periodo del péndulo compuesto para cualquier amplitud.

Empleando la fórmula del coseno del ángulo doble cos2A=cos²A-sin²A, y la relación sin²A+cos²A=1.

$d t = \sqrt{\frac{R}{g}} \frac{d \frac{θ}{2}}{\sqrt{\sin^{2} \frac{θ_{0}}{2} - \sin^{2} \frac{θ}{2}}}$

Haciendo la sustitución

$\begin{array}{l} \sin ϕ = \frac{\sin \frac{θ}{2}}{\sin \frac{θ_{0}}{2}} k = \sin \frac{θ_{0}}{2} \\ \frac{θ}{2} = \arcsin (k \cdot sin ϕ) \frac{d θ}{2} = \frac{k \cos ϕ \cdot d ϕ}{\sqrt{1 - k^{2} \sin^{2} ϕ}} \end{array}$

obtenemos

$d t = \sqrt{\frac{R}{g}} \frac{d ϕ}{\sqrt{1 - k^{2} \sin^{2} ϕ}}$

El tiempo que emplea la partícula en desplazarse desde θ=0, (φ=0) hasta θ₀ (φ=π/2) es la integral elíptica completa de primera especie.

$t = \sqrt{\frac{R}{g}} \int_{0}^{π / 2} \frac{d ϕ}{\sqrt{1 - k^{2} \sin^{2} ϕ}} k = \sin \frac{θ_{0}}{2}$

El tiempo que tarda la partícula desde que sale en la posición –θ₀, con velocidad inicial cero, hasta que llega a la posición final θ₀ es el doble del tiempo 2·t. El periodo de una oscilación completa de la partícula es P=4·t.

El programa interactivo que viene a continuación calcula la integral elíptica completa cuando se proporciona la posición de partida θ₀ de la partícula.

Programa para calcular la integral elíptica completa de primera especie

ForzadasApplet aparecerá en un explorador compatible con JDK 1.1.

Ejemplo:

Para θ₀=60º la integral elíptica vale 1.6858. El tiempo que tarda la partícula en deslizar sin rozamiento sobre la superficie semicircular de radio R=1 m desde la posición -60º hasta 60º es

$t = 2 \sqrt{\frac{1}{9.8}} 1.6858 = 1.08 s$

Para θ₀=15º la integral elíptica vale 1.5776. El tiempo que tarda la partícula en deslizar sin rozamiento sobre la superficie semicircular de radio R=1 m desde la posición -15º hasta 15º es

$t = 2 \sqrt{\frac{1}{9.8}} 1.5776 = 1.01 s$