Movimiento de un cuerpo en el seno de un fluido

Un cuerpo de pequeñas dimensiones se deja caer desde una altura de 5 m sobre la superficie de un estanque de 10 m de profundidad. Dependiendo de su densidad, el cuerpo puede frenarse en el líquido y regresar al punto de partida o bien, puede llegar al fondo del estanque y rebotar elásticamente.

Se ha diseñado un programa interactivo para describir el movimiento de un cuerpo en el seno de un fluido no viscoso, tiene un interés didáctico más allá del principio de Arquímedes, pues nos permite explorar el significado de movimiento acelerado y movimiento decelerado, comparando los signos de la velocidad y de la aceleración.

Ecuaciones del movimiento

Consideremos un cuerpo de pequeñas dimensiones moviéndose verticalmente en un fluido cuya viscosidad es despreciable por tanto, no actúa ninguna fuerzas de rozamiento

Las fuerzas que actúan sobre el cuerpo en el seno del fluido son dos: el peso y el empuje. El empuje se calcula aplicando el principio de Arquímedes. La segunda ley de Newton se escribe

ma=empuje-peso

$ρ_{s} V a = ρ_{f} V g - ρ_{s} V g a = \frac{ρ_{f} - ρ_{s}}{ρ_{s}} g$

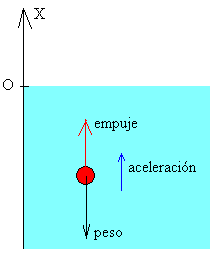Se toma la dirección vertical hacia arriba como eje positivo de las X. Cuando el cuerpo desciende v<0 y cuando asciende v>0.

Se pueden dar los siguientes casos:

Si ρ_s<ρ_f entonces a>0 y con v<0 el cuerpo desciende hasta cierta profundidad máxima y luego, asciende retornando al origen.
Si ρ_s>ρ_f entonces a<0 y con v<0 el cuerpo desciende en el fluido
Si ρ_s=ρ_f el cuerpo a=0 se mueve con movimiento uniforme en el seno del fluido

Formularemos a continuación las ecuaciones del movimiento del cuerpo a lo largo del eje X, tomando como origen la superficie del estanque.

Movimiento de caída libre desde una altura h.

$a = - g v = - g t x = h - \frac{1}{2} g t^{2}$

Cuando llega a la superficie del fluido la velocidad del cuerpo es

$v_{0} = - \sqrt{2 g h}$

Movimiento en el seno del fluido

$v = v_{0} + a t x = v_{0} t + \frac{1}{2} a t^{2}$

Como v₀<0, si a>0 la velocidad v disminuye (en valor absoluto) y se puede hacer cero antes de que el cuerpo llegue al fondo del estanque

No llega al fondo

El tiempo t necesario para que v sea cero y el desplazamiento es,

$t = \frac{| v_{0} |}{a} x = - \frac{v_{0}^{2}}{2 a}$

Si x>-H (profundidad del estanque) el cuerpo no llega al fondo. El cuerpo, sale del fluido con la misma velocidad v₀ y regresa al origen con velocidad final cero.

Rebota en el fondo

El cuerpo llega al fondo, (posición x=-H) en el instante t tal que

-H=v₀t+at²/2

Con una velocidad

v_f=v₀+at (v_f<0)

En ese momento, el cuerpo rebota elásticamente (la velocidad cambia de signo) e inicia su ascensión,

v=-v_f+at (v>0)
x=-H-v_f t+at²/2

saliendo del fluido con la misma velocidad con la que entró v₀, y regresa al punto de partida con velocidad final cero.

Como podemos apreciar en las ecuaciones, se supone que las dimensiones del cuerpo son pequeñas para no tener que considerar el movimiento del cuerpo mientras entra o sale del agua.

Ejemplo

Sea un cuerpo de pequeñas dimensiones, de densidad ρ_s= 0.4 g/cm³=400 kg/m³.

Se deja caer desde una altura de 5 m y llega a la superficie del agua con una velocidad v₀=-9.9 m/s.

Penetra en el fluido, su aceleración es (1000-400)·9.8/400=14.7 m/s². Como la velocidad y aceleración tienen signos contrarios, la velocidad disminuye (en valor absoluto) hasta que se hace cero, 0.67 s más tarde, o en el instante t=1.7 s. Alcanzando una profundidad máxima de x=-3.33 m.

A continuación, asciende, sale del agua con la misma velocidad con la que entró y regresa al punto de partida con velocidad final cero.

Si ahora cambiamos la densidad del cuerpo a 2.0 g/cm³. La velocidad con que llega a la superficie del agua es la misma v₀=-9.9 m/s.

La aceleración en el fluido es (1000-2000)·9.8/2000=-4.9 m/s². Como la velocidad y la aceleración tienen el mismo signo, el cuerpo se acelera. Alcanza el fondo 0.83 s después de pasar por la superficie del estanque, con una velocidad de 14.0 m/s.

Después de rebotar en el fondo del estanque, cambia el signo de su velocidad, llega a la superficie del agua y retorna al punto de partida con velocidad final cero.

Estudio energético

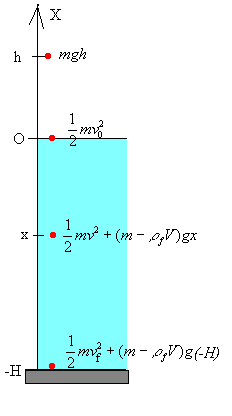Cuando el cuerpo está sometido a la acción de fuerzas conservativas, la energía total se conserva.

La energía potencial se transforma en cinética y la energía cinética en potencial. La energía total, suma de la potencial más la cinética, se mantiene constante.

El peso y el empuje son fuerzas conservativas, la energía total permanece constante

En el aire
Cuando el cuerpo está en el aire la energía potencial vale mgx, donde x es la altura sobre la superficie de fluido.

Cuando el cuerpo llega a la superficie del fluido, su energía potencial se ha convertido en cinética, su velocidad es v₀.

$m g h = \frac{1}{2} m v_{0}^{2} v_{0} = \sqrt{2 g h}$

Si se deja caer el cuerpo desde una altura h=5 m la velocidad con que llega a la superficie del agua es v₀=9.9 m/s.
En el seno de un fluido ideal

Cuando el cuerpo está en el fluido su energía potencial es (mg-ρ _fVg)x. Donde x es la profundidad (valor negativo).

La velocidad del cuerpo en cualquier punto x<0 del fluido es

$\frac{1}{2} m v_{0}^{2} = \frac{1}{2} m v^{2} + (m - ρ_{f} V) g x$

Simplificando el volumen V se obtiene la ecuación

$\frac{1}{2} ρ_{s} v^{2} = \frac{1}{2} ρ_{s} v_{0}^{2} - (ρ_{s} - ρ_{f}) g x$

No llega al fondo del estanque

Si el empuje es mayor que el peso, el cuerpo alcanza una máxima profundidad, poniendo v=0, se despeja x.

$x = \frac{ρ_{s} v_{0}^{2}}{2 (ρ_{s} - ρ_{f}) g}$

Por ejemplo, para ρ_s=0.4 g/cm³, el valor de x=-3.33 m

Llega al fondo del estanque

Por ejemplo, para ρ_s=2.0 g/cm³, el empuje es menor que el peso y alcanza el fondo del estanque x=-10 m. con una velocidad de v=14.0 m/s.

Actividades

Se introduce

la densidad del cuerpo, actuando en la barra de desplazamiento titulada titulado Densidad cuerpo.

Se pulsa el botón titulado Empieza.

Se observa el movimiento del cuerpo, las fuerzas que actúan sobre el mismo. A la derecha del applet, se representa la velocidad y la aceleración en cada instante.

Se sugiere al lector que relacione el movimiento acelerado o decelerado, con los signos de la velocidad y de la aceleración en la representación gráfica.

Se sugiere resolver numéricamente el problema y luego, contrastar los resultados obtenidos con el programa interactivo, en los tres casos siguientes:

Cuando la densidad del cuerpo es menor que la del agua (1.0 g/cm³ )
Cuando la densidad del cuerpo es mayor que la del agua
Cuando la densidad del cuerpo es igual a la del agua.

FluidoApplet1 aparecerá en un explorador compatible con JDK 1.1.