Modos de vibración de una cuerda con cuentas

En esta página, se describen las oscilaciones de una cuerda fijada por ambos extremos con un número de una o dos masas puntuales sujetas a la cuerda. Los problemas de vibraciones de una cuerda no homogénea son difíciles de resolver por lo que solamente daremos los resultados, el lector interesado en conocer la deducción de las frecuencias de los distintos modos de vibración puede consultar el artículo citado en las referencias.

Estos dos ejemplos son interesantes para el lector interesado en el cálculo numérico de las raíces de una ecuación trascendente.

La frecuencia angular de vibración ω y el número de onda k están relacionados

$k = \frac{ω}{v} v = \sqrt{\frac{T}{μ}}$

v es la velocidad de propagación de las ondas trasversales en la cuerda homogénea, T es la tensión y μ la densidad lineal

Una única masa sujeta a la cuerda

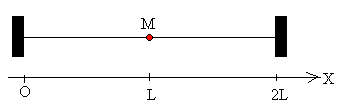
Consideremos una cuerda homogénea de longitud 2L y masa 2m con una masa puntual M situada en la posición x=L, tal como se muestra en la figura.

Las frecuencias de los distintos modos de vibración se calculan del siguiente modo

$\begin{array}{l} F_{1} (k L) = \sin (k L) = 0 \\ F_{2} (k L) = p \cdot \sin (k L) - 2 \cos (k L) = 0 p = \frac{M}{m} k L \end{array}$

Las raíces de la primera ecuación son kL=nπ con n=1, 2, 3…Sus frecuencias son

$f = \frac{ω}{2 π} = \frac{k}{2 π} v$

Para determinar las raíces de la segunda ecuación, es preciso emplear procedimientos numéricos.

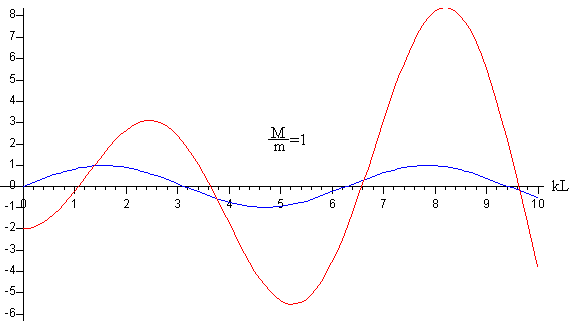
En la figura, se representa la función F₁(kL) en color azul y F₂(kL) en color rojo. Las intersecciones con el eje horizontal son las raíces de las ecuaciones en este caso, para M/m=1.

La amplitud en los distintos puntos x de la cuerda correspondiente a los modos de vibración solución de la primera ecuación es

$Φ (x) = {\begin{cases} A \sin (k x) 0 \leq x \leq L \\ A \sin (k (x - 2 L)) L \leq x \leq 2 L \end{cases}$

Las frecuencias de los distintos modos de vibración coinciden con los de una cuerda homogénea de longitud 2L teniendo índice par. Tales modos presentan un nodo en la posición x=L y por tanto, no se alteran por la presencia de la masa puntual M.

$f_{n} = \frac{n}{2 (2 L)} v n = 2,4,6...$

La amplitud en los distintos puntos x de la cuerda correspondiente a los modos de vibración solución de la segunda ecuación trascendente es

$Φ (x) = {\begin{cases} A \sin (k x) 0 \leq x \leq L \\ - A \sin (k (x - 2 L)) L \leq x \leq 2 L \end{cases}$

Actividades

Se introduce

El cociente de masas M/m (masa puntual dividido por la masa de una porción de la cuerda de longitud L) actuando en la barra de desplazamiento titulada Cociente M/m
La longitud de la porción L de cuerda se ha fijado en L=1 m
La velocidad de propagación de las ondas trasversales en la cuerda se ha fijado en v=1 m/s. El valor numérico del número de onda k coincide con el valor de la frecuencia angular ω, para calcular la frecuencia de los distintos modos de vibración f=ω/(2π)

Se pulsa el botón titulado Inicio

Se pulsa el botón titulado Siguiente, para observar el siguiente modo de vibración.

Se pulsa el botón titulado Anterior, para observar el modo de vibración anterior

En la parte superior del applet, se muestra el modo de vibración y su frecuencia f en Hz.

Dos masas sujetas a la cuerda

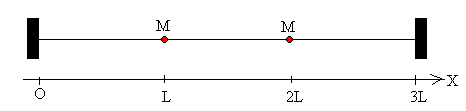
Consideremos una cuerda homogénea de longitud 3L y masa 3m con dos masas puntuales M situadas en las posiciones x=L y x=2L tal como se muestra en la figura.

Las frecuencias de los distintos modos de vibración se calculan del siguiente modo

$\begin{array}{l} F_{1} (k L) = \sin (k L) = 0 \\ F_{2} (k L) = p \cdot \sin (k L) - 2 \cos (k L) - 1 = 0 \\ F_{3} (k L) = p \cdot \sin (k L) - 2 \cos (k L) + 1 = 0 \end{array}$

Las raíces de la primera ecuación son kL=nπ con n=1, 2, 3…

Para determinar las raíces de la segunda y tercera ecuación, es preciso emplear procedimientos numéricos.

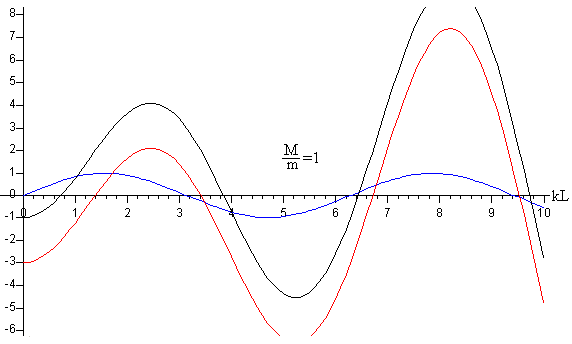
En la figura, se representa la función F₁(kL) en color azul y F₂(kL) en color rojo y F₃(kL) en color negro. Las intersecciones con el eje horizontal son las raíces de las ecuaciones en este caso, para M/m=1.

La amplitud en los distintos puntos x de la cuerda correspondiente a los modos de vibración solución de la primera ecuación es

$Φ (x) = A \sin (k x) 0 \leq x \leq 3 L$

Las frecuencias de los distintos modos de vibración coinciden con los de una cuerda homogénea de longitud 3L teniendo índice múltiplo de tres. Tales modos presentan un nodo en la posición x=L y otro en la posición x=2L, y por tanto, no se alteran por la presencia de las masas puntuales M.

$f_{n} = \frac{n}{2 (3 L)} v n = 3,6,9,...$

La amplitud en los distintos puntos x de la cuerda correspondiente a los modos de vibración solución de la segunda ecuación es

$Φ (x) = {\begin{cases} A \sin (k x) 0 \leq x \leq L \\ 2 A \cos (\frac{1}{2} k L) \sin (k (\frac{3}{2} L - x)) L \leq x \leq 2 L \\ - A \sin (k (3 L - x)) 2 L \leq x \leq 3 L \end{cases}$

La amplitud en los distintos puntos x de la cuerda correspondiente a los modos de vibración solución de la tercera ecuación es

$Φ (x) = {\begin{cases} A \sin (k x) 0 \leq x \leq L \\ 2 A \sin (\frac{1}{2} k L) \cos (k (\frac{3}{2} L - x)) L \leq x \leq 2 L \\ A \sin (k (3 L - x)) 2 L \leq x \leq 3 L \end{cases}$