• Inicio
• Movimiento ondulatorio
• Propagación

Ondas estacionarias en una cuerda no homogénea

En esta página, estudiamos las ondas estacionarias producidas en una cuerda no homogénea sujeta por ambos extremos. La cuerda de longitud 2L está formada por dos mitades de la misma longitud L pero de distinta densidad lineal m₁ y m₂ respectivamente. La tensión T de la cuerda es igual al peso que cuelga de su extremo derecho.

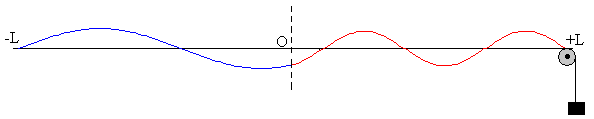
Solución de la ecuación diferencial del movimiento ondulatorio

Las ecuaciones diferenciales del movimiento ondulatorio, son respectivamente

${\displaystyle v_1^2\frac{{\partial }^2{\Psi }_1}{\partial x^2}=\frac{{\partial }^2{\Psi }_1}{\partial t^2}{v}_2^2\frac{{\partial }^2{\Psi }_2}{\partial x^2}=\frac{{\partial }^2{\Psi }_2}{\partial t^2}}$

Ψ es el desplazamiento trasversal de un punto x de la cuerda en el instante t.

v₁ y v₂ son las velocidades de propagación de las ondas trasversales en las partes izquierda y derecha de la cuerda

${\displaystyle v_1=\sqrt{\frac{T}{m_1}}{v}_2=\sqrt{\frac{T}{m_2}}}$

Siguiendo los mismos pasos que para una cuerda homogénea sujeta por ambos extremos, ensayamos la solución

Ψ(x,t)=y(x)sin(ωt)

que describe una onda estacionaria. Cada punto de la cuerda vibra con una amplitud y(x) y con frecuencia angular ω.

Introduciendo esta expresión en cada una de las dos ecuaciones diferenciales del movimiento ondulatorio obtenemos las ecuaciones diferenciales similares a las de un M.A.S.

${\displaystyle \frac{d^2{y}_1}{d{x}^2}+\frac{{\omega }^2}{v_1^2}{y}_1=0\frac{d^2{y}_2}{d{x}^2}+\frac{{\omega }^2}{v_2^2}{y}_2=0}$

Las soluciones de estas ecuaciones diferenciales son

y₁(x)=A₁sin (k₁x)+B₁cos(k₁x) 
y₂(x)=A₂sin (k₂x)+B₂cos(k₂x) 

k₁=ω/v₁  y k₂=ω/v₂  son los números de onda, respectivos

Los coeficientes A₁, B₁, A₂ y B₂, vienen determinados por la continuidad de la función de onda en x=0, y por las condiciones de contorno en los extremos fijos x=-L y x=+L.

Continuidad de la función que describe la onda estacionaria

En el punto x=0, las dos mitades de la cuerda se unen. La función que describe la onda estacionaria tiene que ser continua y también su derivada primera.

${\displaystyle \begin{array}{l}{y}_1(0)=y_2(0)B_1=B_2\\ {\frac{\partial y_1}{\partial x}|}_{x=0}={\frac{\partial y_2}{\partial x}|}_{x=0}{k}_1{A}_1=k_2{A}_2\end{array}}$

La función que describe la amplitud de la onda estacionaria y(x) en cada una de las dos partes de la cuerda es

${\displaystyle \begin{array}{l}{y}_1(x)=A_1\sin (k_{1}x)+B_1\cos (k_{1}x)\\ y_2(x)=A_1\left(\frac{k_1}{k_2}\right)\sin (k_{2}x)+B_1\cos (k_{2}x)\end{array}}$

Condiciones de contorno

El extremo izquierdo de la cuerda está sujeto en x=-L y el extremo derecho en x=+L. Se tiene que cumplir que

${\displaystyle \begin{array}{l}{y}_1(-L)=0y_2(+L)=0\\ A_1\sin (k_{1}L)=B_1\cos (k_{1}L)\\ A_1\left(\frac{k_1}{k_2}\right)\sin (k_{2}L)=-B_1\cos (k_{2}L)\end{array}}$

Dividiendo miembro a miembro eliminamos A₁ y B₁.

${\displaystyle \begin{array}{l}\frac{k_2}{k_1}\frac{\text{sin}(k_{1}L)}{\text{sin}(k_{2}L)}=-\frac{\cos (k_{1}L)}{\cos (k_{2}L)}\\ v_1\frac{\text{sin}(\omega L/v_1)}{\cos (\omega L/v_1)}=-v_2\frac{\text{sin}(\omega L/v_2)}{\cos (\omega L/v_2)}\end{array}}$

Frecuencias de los modos de vibración de la cuerda

Para calcular las frecuencias de los modos de vibración de la cuerda se resuelve la ecuación trascendente

${\displaystyle v_1\tan \left(\frac{\omega L}{v_1}\right)=-v_2\tan \left(\frac{\omega L}{v_2}\right)}$

Se dibujan las funciones

z=v₁tan(2πfL/v₁)
z=v₂tan(2πfL/v₂)

en función de la frecuencia  f .

Las abscisas de los puntos de intersección son las frecuencias f₁, f₂, f₃, …  de los distintos modos de vibración tal como se muestra en la figura.

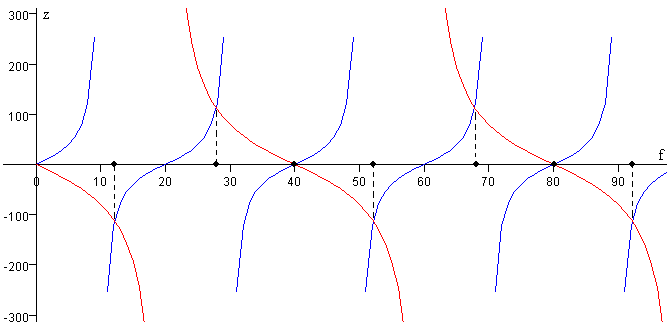
En la figura, se representa la primera función para v₁=40 m/s (en azul), y la segunda para v₂=80 m/s (en rojo), en ambos casos, la longitud de cada una de las dos mitades de la cuerda es L= 1m.

Se ha empleado el procedimiento numérico del el punto medio para calcular las frecuencias. Para ello, hay que calcular las raíces de la ecuación trascendente

${\displaystyle v_1\tan \left(\frac{\omega L}{v_1}\right)+v_2\tan \left(\frac{\omega L}{v_2}\right)=0}$

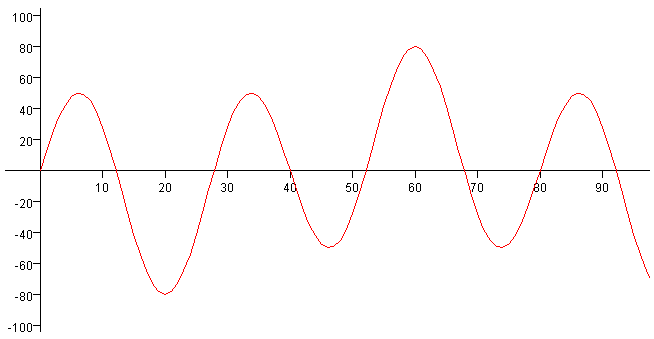
Una representación gráfica de esta función, nos sugiere que esta no es una forma conveniente, para aplicar dicho procedimiento numérico, ya que la función tangente crece rápidamente con el argumento. Expresamos la ecuación anterior de la forma equivalente

${\displaystyle v_1\sin \left(\frac{\omega L}{v_1}\right)\cos \left(\frac{\omega L}{v_2}\right)+v_2\sin \left(\frac{\omega L}{v_2}\right)\cos \left(\frac{\omega L}{v_1}\right)=0}$

En la figura, se representa esta función en función de la frecuencia f, ω=2πf cuando v₁=40 m/s v₂=80 m/s  y L=1 m. Los ceros de la función, los puntos de corte con el eje horizontal son las frecuencias f₁, f₂, f₃, …de los distintos modos de vibración: 12.2, 27.8, 40.0, 52.2, 67.8, 80.0,.. Hz

 

Amplitud de las ondas estacionarias

Despejamos A₁, en las dos ecuaciones que resultan de aplicar las condiciones de contorno, y la sustituimos en las dos funciones que describen la amplitud de la onda estacionaria y(x) en cada una de las dos partes de la cuerda

Para el modo de vibración ω=2πf_.

${\displaystyle \begin{array}{l}{y}_1(x)=B_1\left\{\cos \left(\frac{\omega x}{v_1}\right)+\frac{\text{cos}(\omega L/v_1)}{\text{sin}(\omega L/v_1)}\text{sin}\left(\frac{\omega x}{v_1}\right)\right\}\\ y_2(x)=B_1\left\{\cos \left(\frac{\omega x}{v_2}\right)-\frac{\text{cos}(\omega L/v_2)}{\text{sin}(\omega L/v_2)}\text{sin}\left(\frac{\omega x}{v_2}\right)\right\}\end{array}}$

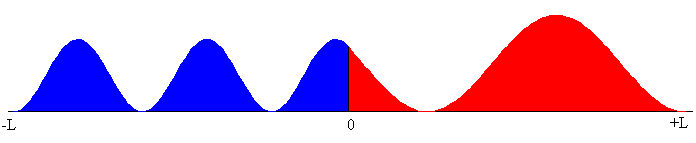
B₁ es un factor de escala. Para que todos los modos de vibración se representen a la misma escala se calcula B₁ de modo que el área bajo la curva

${\displaystyle {\displaystyle \underset{-L}{\overset{0}{\int }}{y}_1^2(x)dx+}{\displaystyle \underset{0}{\overset{L}{\int }}{y}_2^2(x)dx}=1}$

La integral definida de la izquierda es el área sombreada en color azul y la integral de la derecha es el área sombreada en color rojo.

Después de realizar algunas operaciones se llega al siguiente resultado

${\displaystyle B_1^2\left\{\begin{array}{l}\frac{1}{2}\left(L+\frac{v_1}{2\omega }\text{sin}\left(\frac{\omega L}{v_1}\right)\right)+\frac{1}{2}{\left(\frac{\text{cos}(\omega L/v_1)}{\text{sin}(\omega L/v_1)}\right)}^2\left(L-\frac{v_1}{2\omega }\text{sin}\left(\frac{\omega L}{v_1}\right)\right)\\ -\frac{v_1}{2\omega }\left(\frac{\text{cos}(\omega L/v_1)}{\text{sin}(\omega L/v_1)}\right)(1-\text{sin}\left(\frac{2\omega L}{v_1}\right)+\\ \frac{1}{2}\left(L+\frac{v_2}{2\omega }\text{sin}\left(\frac{\omega L}{v_2}\right)\right)+\frac{1}{2}{\left(\frac{\text{cos}(\omega L/v_2)}{\text{sin}(\omega L/v_2)}\right)}^2\left(L-\frac{v_2}{2\omega }\text{sin}\left(\frac{\omega L}{v_2}\right)\right)\\ -\frac{v_2}{2\omega }\left(\frac{\text{cos}(\omega L/v_2)}{\text{sin}(\omega L/v_2)}\right)(1-\text{sin}\left(\frac{2\omega L}{v_2}\right)\end{array}\right\}=1}$

Para obtener este resultado, se ha empleado las integrales siguientes:

${\displaystyle \begin{array}{l}{\displaystyle \underset{-L}{\overset{0}{\int }}{\cos }^2(k_{1}x)dx}=\frac{1}{2}\left(L+\frac{1}{2k_1}\text{sin}(2k_{1}L)\right)\\ {\displaystyle \underset{-L}{\overset{0}{\int }}{\text{sin}}^2(k_{1}x)dx}=\frac{1}{2}\left(L-\frac{1}{2k_1}\text{sin}(2k_{1}L)\right)\\ {\displaystyle \underset{-L}{\overset{0}{\int }}\text{sin}(2k_{1}x)dx}=-\frac{1}{2k_1}\left(1-\cos (2k_{1}L)\right)k_1=\frac{\omega }{v_1}\end{array}}$

y de modo similar, para la parte derecha de la cuerda

Casos especiales

Para ciertas frecuencias puede ocurrir que sen(ωL/v₁) y sen(ωL/v₂) sean ambos cero a la vez. Por ejemplo, cuando v₁=40 m/s y v₂=80 m/s con L=1 m tenemos que

sin(ωL/v₁)=0 para 2πf₁L/v₁=n₁π donde n₁ es un entero. Las frecuencias  f₁=20n₁ son

 f₁=20, 40, 60, 80, 100,…Hz

sin(ωL/v₂)=0 para 2πf₂L/v₂=n₂π donde n₂ es un entero. Las frecuencias  f₂=40n₂ son

f₂=40, 80, … Hz

Las frecuencias comunes son f₁= f₂=40, 80, 120… Hz

Las frecuencias especiales son aquellas  f₁=n₁v₁/(2L) y f₂=n₂v₂/(2L) para las cuales se cumple que n₁v₁=n₂v₂ donde n₁ y n₂ son enteros

Corresponden a los modos de vibración de la cuerda para las cuales el área se hace infinita y B₁ tiende a cero. Pero la amplitud y(x) del modo de vibración no es cero sino una expresión que vamos a calcular a continuación

En la ecuación trascendente que calcula las frecuencias de los modos de vibración cuando

sin(ωL/v₁) =sin(ωL/v₂)

se cumple que

v₁·cos(ωL/v₂) +v₂·cos(ωL/v₁)=0

Tenemos la igualdad

${\displaystyle \frac{\text{cos}(\omega L/v_2)}{\text{sin}(\omega L/v_2)}=-\frac{v_2}{v_1}\frac{\text{cos}(\omega L/v_1)}{\text{sin}(\omega L/v_1)}}$

que introducimos en la larga expresión que calcula el factor de escala B₁,

${\displaystyle B_1^2\left\{\begin{array}{l}\frac{1}{2}\left(L+\frac{v_1}{2\omega }\text{sin}\left(\frac{\omega L}{v_1}\right)\right)+\frac{1}{2}{\left(\frac{\text{cos}(\omega L/v_1)}{\text{sin}(\omega L/v_1)}\right)}^2\left(L-\frac{v_1}{2\omega }\text{sin}\left(\frac{\omega L}{v_1}\right)\right)\\ -\frac{v_1}{2\omega }\left(\frac{\text{cos}(\omega L/v_1)}{\text{sin}(\omega L/v_1)}\right)(1-\text{sin}\left(\frac{2\omega L}{v_1}\right)+\\ \frac{1}{2}\left(L+\frac{v_2}{2\omega }\text{sin}\left(\frac{\omega L}{v_2}\right)\right)+\frac{1}{2}{\left(\frac{v_2}{v_1}\right)}^2{\left(\frac{\text{cos}(\omega L/v_1)}{\text{sin}(\omega L/v_1)}\right)}^2\left(L-\frac{v_2}{2\omega }\text{sin}\left(\frac{\omega L}{v_2}\right)\right)\\ +\frac{v_2}{2\omega }\left(\frac{v_2}{v_1}\right)\left(\frac{\text{cos}(\omega L/v_1)}{\text{sin}(\omega L/v_1)}\right)(1-\text{sin}\left(\frac{2\omega L}{v_2}\right)\end{array}\right\}=1}$

a continuación, sacamos factor común al cociente

${\displaystyle c=\frac{\text{cos}(\omega L/v_1)}{\text{sin}(\omega L/v_1)}}$

${\displaystyle B_1^2{c}^2\left\{\begin{array}{l}\frac{1}{2c^2}\left(L+\frac{v_1}{2\omega }\text{sin}\left(\frac{\omega L}{v_1}\right)\right)+\frac{1}{2}\left(L-\frac{v_1}{2\omega }\text{sin}\left(\frac{\omega L}{v_1}\right)\right)\\ -\frac{1}{c}\frac{v_1}{2\omega }(1-\text{sin}\left(\frac{2\omega L}{v_1}\right)+\frac{1}{2c^2}\left(L+\frac{v_2}{2\omega }\text{sin}\left(\frac{\omega L}{v_2}\right)\right)+\\ \frac{1}{2}{\left(\frac{v_2}{v_1}\right)}^2\left(L-\frac{v_2}{2\omega }\text{sin}\left(\frac{\omega L}{v_2}\right)\right)+\frac{1}{c}\frac{v_2}{2\omega }\left(\frac{v_2}{v_1}\right)(1-\text{sin}\left(\frac{2\omega L}{v_2}\right)\end{array}\right\}=1}$

Cuando sin(ωL/v₁)→0 o el cociente c→∞, obtenemos 

${\displaystyle \begin{array}{l}{B}_1^2{\left(\frac{\text{cos}(\omega L/v_1)}{\text{sin}(\omega L/v_1)}\right)}^2\left\{\frac{L}{2}+{\left(\frac{-v_2}{v_1}\right)}^2\frac{L}{2}\right\}=1\\ B_1=\frac{\text{sin}(\omega L/v_1)}{\text{cos}(\omega L/v_1)}CC=\frac{1}{\sqrt{\frac{L}{2}\left(1+{\left(\frac{v_2}{v_1}\right)}^2\right)}}\end{array}}$

La amplitud de los modos de vibración para estas frecuencias especiales es

${\displaystyle \begin{array}{l}{y}_1(x)=C\frac{\text{sin}(\omega L/v_1)}{\text{cos}(\omega L/v_1)}\left\{\cos \left(\frac{\omega x}{v_1}\right)+\frac{\text{cos}(\omega L/v_1)}{\text{sin}(\omega L/v_1)}\text{sin}\left(\frac{\omega x}{v_1}\right)\right\}\\ y_2(x)=C\frac{\text{sin}(\omega L/v_1)}{\text{cos}(\omega L/v_1)}\left\{\cos \left(\frac{\omega x}{v_2}\right)+\frac{v_2}{v_1}\frac{\text{cos}(\omega L/v_1)}{\text{sin}(\omega L/v_1)}\text{sin}\left(\frac{\omega x}{v_2}\right)\right\}\end{array}}$

Cuando sin(ωL/v₁)→0

${\displaystyle \begin{array}{l}{y}_1(x)=C\text{sin}(\omega x/v_1)\\ y_2(x)=C\frac{v_2}{v_1}\text{sin}(\omega x/v_2)\end{array}}$

que como podemos comprobar, cumple las condiciones de continuidad en x=0 y las de contorno en x=-L y en x=L.

Actividades

Se introduce

• La velocidad de propagación v₁ de las ondas en la parte izquierda de la cuerda, actuando en la barra de desplazamiento titulada Velocidad 1.

• La velocidad de propagación v₂ de las ondas en la parte izquierda de la cuerda, actuando en la barra de desplazamiento titulada Velocidad 2.

• La longitud de cada una de las dos mitades de la cuerda se ha fijado en L=1 m.

Se pulsa el botón titulado Inicio

Se calculan las frecuencias de los distintos modos de vibración de la cuerda utilizando el procedimiento numérico del punto medio.

Se representa el modo fundamental de vibración de la cuerda de frecuencia ω=2πf₁

Ψ₁(x,t)=y₁(x)sin(ωt)  en el intervalo -L<x<0
Ψ₂(x,t)=y₂(x)sin(ωt) en el intervalo 0<x<+L

Se representan los otros modos de vibración de frecuencias f₂, f₃, f₄ ..., pulsando en el botón titulado Siguiente>>  y Anterior<<.

Referencias

Clendenning L. M. A laboratory approach to eigenvalue problem. Am. J. Phys. 36 (10) October 1968, pp. 879-881

Curso Interactivo de Física en Internet © Ángel Franco García