• Inicio
• Oscilaciones
• Osciladores lineales

Oscilaciones forzadas

En una página anterior, se ha descrito el oscilador amortiguado, la oscilación desaparece al cabo de un cierto tiempo, teóricamente infinito. En esta sección se describe el mecanismo que permite mantener la oscilación.

Disponemos de un motor de velocidad angular variable ω_f. El eje M del motor está situado a una distancia horizontal c y vertical a del eje O del anillo de cobre donde situamos el origen. Una excéntrica de radio r=|MB| está unida a una biela AB. El extremo A de la biela de longitud b está unida a una varilla excitadora AP que puede girar alrededor del eje O. La distancia R=OA se puede modificar mediante un tornillo que sujeta el extremo A de la biela a una ranura existente en la varilla. Modificando R se modifica la amplitud de la fuerza oscilante.

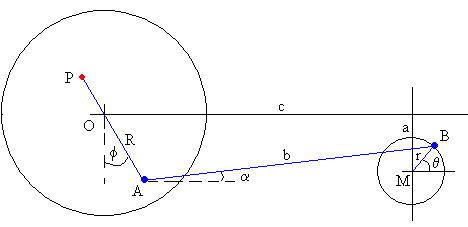
Como el motor gira con velocidad angular constante, en un determinado instante el ángulo que forma la excéntrica con la horizontal θ=ω_f.·t. Dado el ángulo θ, calcularemos el ángulo φ, que forma la varilla con la vertical.

Sea α el ángulo que forma la biela con la horizontal,

R·cosφ-b·sinα=a-r·sinθ
R·sinφ+b·cosα=c+r·cosθ

Eliminamos el ángulo α de este sistema de dos ecuaciones

(Rcosφ-a+rsinθ)²+(c+rcosθ-Rsinφ)²=b²

y teniendo en cuenta que φ es un ángulo pequeño, por lo que sinφ≈φ y cosφ≈0

${\displaystyle \varphi =\frac{R^2+r^2+a^2+c^2-b^2-2Ra+2Rr\text{sin}\theta -2ar\text{sin}\theta +2cr\cos \theta }{2cR+2rR\cos \theta }}$

En la figura, se muestra la gráfica del ángulo de la fuerza φ en función de θ, para los siguientes datos r=1.0, b=22.0, a=10.0, c=22.0,

• La curva roja se ha trazado para R=7.0

• La curva azul se ha trazado para R=12.0

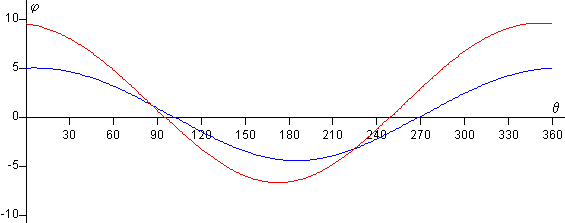
Ambas curvas difieren de un MAS, aunque pueden hacerse próximas a un MAS con una elección apropiada de los parámetros.

Como vemos en la figura, cambiando R, la distancia entre el eje de rotación del anillo de cobre O y el extremo A de la biela cambia la amplitud de la fuerza oscilante.

En la simulación supondremos que la fuerza oscilante produce un momento respecto del eje de rotación del anillo, descrito por la función armónica

M_f=M_0f·cos(ω_f·t)

siendo M_0f· la amplitud y ω_f la frecuencia angular.

La ecuación del movimiento del disco se escribe ahora

Iα=-kθ- λω+M_f

• α  es la aceleración angular del disco cuando el indicador del péndulo se encuentra en la posición angular θ.

• I es el momento de inercia del anillo respecto del eje de rotación

• k es la constante del muelle helicoidal

• λω es el momento de rozamiento proporcional a la velocidad angular ω de rotación, debidos a las corrientes de Foucault producidas en el disco de cobre por el campo magnético de la bobina.

• M_f es el momento de la fuerza oscilante producida por el motor respecto del eje de rotación O.

Expresamos la ecuación del movimiento en forma de ecuación diferencial

${\displaystyle \frac{d^2\theta }{d{t}^2}+2\gamma \frac{d\theta }{dt}+{\omega }_0^2\theta =\frac{M_{0f}}{I}\text{cos(}{\omega }_{f}t){\omega }_{\text{0}}^{\text{2}}=\frac{k}{I}2\gamma =\frac{\lambda }{I}}$

• donde ω₀ es la frecuencia natural o propia del oscilador
• ω_f es la frecuencia angular del momento producido por la fuerza oscilante de amplitud M_0f
• γ es la constante de amortiguamiento, ${\gamma }^2<{\omega }_0^2$

Como mostramos en la página titulada “El estado transitorio y su evolución hacia el estado estacionario”, la solución de la ecuación diferencial con las condiciones iniciales θ=0, y dθ/dt=0 en el instante t=0, el indicador del anillo parte del origen con velocidad angular inicial nula, es

${\displaystyle \theta =\frac{M_{0f}}{I\left({({\omega }_0^2-{\omega }_f^2)}^2+4{\gamma }^2{\omega }_f^2\right)}\left\{\begin{array}{l}({\omega }_0^2-{\omega }_f^2)\left(\cos ({\omega }_{f}t)-\exp (-\gamma t)\cos (\omega t)\right)+\\ 2\gamma {\omega }_f\left(\text{sin}({\omega }_{f}t)-\frac{{\omega }_0^2+{\omega }_f^2}{2\omega {\omega }_f}\exp (-\gamma t)\text{sin}(\omega t)\right)\end{array}\right\}}$

Actividades

Se introduce,

• La intensidad i de la corriente que pasa por la bobina, lo que equivale a una constante de amortiguamiento γ=1.396·i²

• La frecuencia del momento de la fuerza oscilante f, actuando en la barra de desplazamiento titulada Frecuencia fuerza, ω_f=2πf rad/s.

• La frecuencia propia o natural del oscilador se mantiene fija e igual a, f₀=0.5 Hz, ω₀=π rad/s

• La amplitud del momento de la fuerza oscilante M_0f/I, actuando en la barra de desplazamiento titulada Amplitud.

Se puede elegir entre

• la representación gráfica de la posición del indicador θ en función del tiempo t, activando la casilla titulada Gráfica,

• la simulación del oscilador forzado, cuando dicha casilla se encuentra desactivada.

Se pulsa el botón titulado Empieza

Manteniendo fija la intensidad i de la corriente que pasa por la bobina (o la constante de amortiguamiento γ), y la amplitud M_0f del momento de la fuerza oscilante, y con la casilla Gráfica activada, medimos la amplitud de la oscilación forzada en el estado estacionario para varios valores de la frecuencia de la fuerza oscilante ω_f, completando tablas similares a la siguiente:

Intensidad i=
Cociente ωf/ω0	Amplitud (estado estacionario)
1.0

Se representa los datos de dos tablas en la misma gráfica, empleando distintos colores para cada gráfica.

ForzadasApplet aparecerá en un explorador compatible con JDK 1.1.

Curso Interactivo de Física en Internet © Ángel Franco García