• Inicio
• Oscilaciones
• Osciladores lineales

El estado transitorio y su evolución hacia el estado estacionario

Esta página es interesante para aquellos lectores a los que les guste

• realizar operaciones con funciones trigonométricas,
• calcular derivadas de una función,
• límites,
• simplificar expresiones,
• obtener una expresión más simple para casos particulares de otra general más compleja.

Solución de la ecuación diferencial

La ecuación diferencial que describe las oscilaciones forzadas es

${\displaystyle \frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=\frac{F}{m}\cos ({\omega }_{f}t)}$

• donde ω₀ es la frecuencia natural o propia del oscilador
• ω_f es la frecuencia angular de la fuerza oscilante de amplitud F
• γ es la constante de amortiguamiento,  γ<ω₀

La solución general de la ecuación diferencial homogénea tiene la forma

${\displaystyle x_1=(C\cos (\omega t)+D\text{sin}(\omega t))·\exp (-\gamma t)\omega =\sqrt{{\omega }_0^2-{\gamma }^2}}$

Donde los coeficientes C y D se determinan a partir de las condiciones iniciales

Una solución particular de la ecuación diferencial completa tiene la forma

x₂=Acos(ω_f t)+Bsin(ω_f t)

Obtendremos los valores de A y B haciendo que cumpla la ecuación diferencial lineal completa

${\displaystyle A=\frac{F({\omega }_0^2-{\omega }_f^2)}{m\left({({\omega }_0^2-{\omega }_f^2)}^2+4{\gamma }^2{\omega }_f^2\right)}B=\frac{2\gamma {\omega }_{f}F}{m\left({({\omega }_0^2-{\omega }_f^2)}^2+4{\gamma }^2{\omega }_f^2\right)}}$

La solución general de la ecuación diferencial completa es la suma de la solución general de la homogénea más la solución particular x=x₁+x₂.

${\displaystyle x=\left(C\cos (\omega t)+D\text{sin}(\omega t)\right)\exp (-\gamma t)+A\cos ({\omega }_{f}t)+B\text{sin}({\omega }_{f}t)}$

El primer término, describe el estado transitorio que desaparece al cabo de cierto tiempo (teóricamente infinito) y depende de las condiciones iniciales. El segundo término, describe el estado estacionario.

La velocidad vale

${\displaystyle v=\frac{dx}{dt}=\{\begin{array}{l}-A{\omega }_f\sin ({\omega }_{f}t)+{\omega }_{f}B\cos ({\omega }_{f}t)\\ -\gamma \left(C\cos (\omega t)+D\text{sin}(\omega t)\right)\exp (-\gamma t)+\left(-\omega C\sin (\omega t)+\omega D\cos (\omega t)\right)\exp (-\gamma t)\end{array}}$

Si las condiciones iniciales son t=0, x=x₀, v=v₀.

${\displaystyle \begin{array}{l}C=x_0-A\\ D=\frac{1}{\omega }(v_0+\gamma C-{\omega }_{f}B)\end{array}}$

Las condiciones iniciales más sencillas son x=0, y dx/dt=0 en el instante t=0. La partícula de masa m parte del origen con velocidad inicial nula.

${\displaystyle C=-\frac{F({\omega }_0^2-{\omega }_f^2)}{m\left({({\omega }_0^2-{\omega }_f^2)}^2+4{\gamma }^2{\omega }_f^2\right)}D=-\frac{F\gamma ({\omega }_0^2+{\omega }_f^2)}{m\omega \left({({\omega }_0^2-{\omega }_f^2)}^2+4{\gamma }^2{\omega }_f^2\right)}}$

La posición de la partícula x que experimenta una oscilación forzada en función del tiempo t es

${\displaystyle x=\frac{F}{m\left({({\omega }_0^2-{\omega }_f^2)}^2+4{\gamma }^2{\omega }_f^2\right)}\left(\begin{array}{l}({\omega }_0^2-{\omega }_f^2)\left(\cos ({\omega }_{f}t)-\exp (-\gamma t)\cos (\omega t)\right)+\\ 2\gamma {\omega }_f\left(\text{sin}({\omega }_{f}t)-\frac{{\omega }_0^2+{\omega }_f^2}{2\omega {\omega }_f}\exp (-\gamma t)\text{sin}(\omega t)\right)\end{array}\right)}$

Vamos a obtener expresiones más simples para casos particulares.

No hay rozamiento γ=0

Vamos a estudiar dos casos, cerca de la frecuencia de la resonancia y en la resonancia

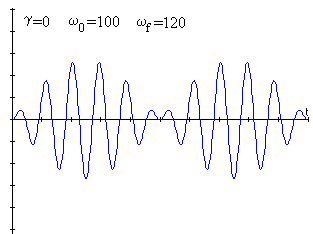
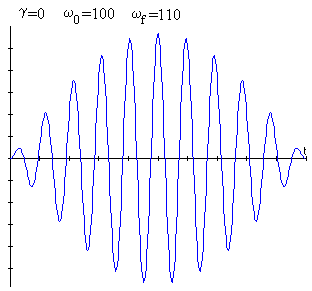
Cerca de la resonancia ω_f=ω₀+ε con ε< ω₀

Si no hay rozamiento, la frecuencia angular de la oscilación amortiguada ω, es igual a la de la oscilación libre, ω_0. Como la diferencia ε entre la frecuencia ω_f de la fuerza oscilante y la de resonancia ω₀ es pequeña, se puede hacer la siguiente aproximación

${\displaystyle {\omega }_0^2-{\omega }_f^2=({\omega }_0+{\omega }_f)({\omega }_0-{\omega }_f)\approx -2{\omega }_0\epsilon }$

Empleando la siguiente relación trigonométrica

${\displaystyle \cos A-\cos B=2\text{sin}\left(\frac{B+A}{2}\right)\text{sin}\left(\frac{B-A}{2}\right)}$

se obtiene finalmente,

${\displaystyle x=\frac{F}{m{\omega }_0\epsilon }\text{sin}\left(\frac{\epsilon t}{2}\right)\text{sin}({\omega }_{0}t)}$

La amplitud (el producto de los dos primeros términos) y la frecuencia de las pulsaciones se determinan por el grado de cercanía a la frecuencia de resonancia tal como se puede apreciar en las figuras.

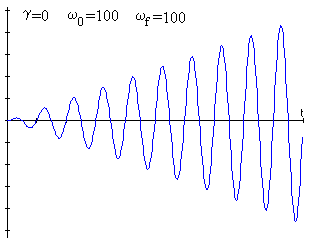
En la resonancia ω_f=ω₀

En la fórmula del desplazamiento x(t) tomamos el siguiente límite

${\displaystyle \epsilon \to 0\text{sen}\left(\frac{\epsilon t}{2}\right)\to \frac{\epsilon t}{2}}$

La amplitud crece linealmente con el tiempo, como puede verse en la figura

${\displaystyle x=\frac{F}{2m{\omega }_0}t\text{ sin}({\omega }_{0}t)}$

Cuando hay rozamiento

Vamos a estudiar dos casos, cerca de la frecuencia de la resonancia y en la resonancia. Comprobaremos que el sistema llega a oscilaciones estables al cabo de un cierto tiempo t del orden de 1/γ.

Cerca de la resonancia ω_f=ω₀+ε con ε< ω₀

Si la constante de amortiguamiento γ es pequeña, la frecuencia angular de la oscilación amortiguada ω es casi igual a la de la oscilación libre ω₀, de modo que ω≈ω₀. Como la diferencia ε entre la frecuencia ω_f de la fuerza oscilante y la de resonancia ω₀ es pequeña, se puede hacer la siguiente aproximación

${\displaystyle {\omega }_0^2-{\omega }_f^2=({\omega }_0+{\omega }_f)({\omega }_0-{\omega }_f)\approx -2{\omega }_0\epsilon }$

La solución de la ecuación diferencial completa con estas aproximaciones nos queda.

${\displaystyle x=\frac{F}{m\left(4{\omega }_0^2{\epsilon }^2+4{\gamma }^2{\omega }_0^2\right)}\left(\begin{array}{l}-2{\omega }_0\epsilon \left(\cos ({\omega }_{f}t)-\exp (-\gamma t)\cos ({\omega }_{0}t)\right)+\\ 2\gamma {\omega }_0\left(\text{sin}({\omega }_{f}t)-\exp (-\gamma t)\text{sin}({\omega }_{0}t)\right)\end{array}\right)}$

Cambiando el orden de los términos

${\displaystyle x=\frac{F}{2m{\omega }_0\left({\epsilon }^2+{\gamma }^2\right)}\left(\begin{array}{l}-\exp (-\gamma t)\left(-\epsilon \cos ({\omega }_{0}t)+\gamma \text{sin}({\omega }_{0}t)\right)+\\ \left(-\epsilon \cos ({\omega }_{f}t)+\gamma \text{sin}({\omega }_{f}t)\right)\end{array}\right)}$

Podemos escribir la suma de seno y coseno de los términos entre paréntesis de la siguiente modo

${\displaystyle -\epsilon \cos ({\omega }_{0}t)+\gamma \text{sin}({\omega }_{0}t)=\sqrt{{\epsilon }^2+{\gamma }^2}\text{sin}\left({\omega }_{0}t+\varphi \right)\text{tan}\varphi =\frac{\text{-}\epsilon }{\gamma }}$

y de modo similar, el segundo término entre paréntesis de frecuencia angular ω_f.

${\displaystyle x=\frac{F}{2m{\omega }_0\sqrt{{\epsilon }^2+{\gamma }^2}}\left(-\exp (-\gamma t)\text{sin}({\omega }_{0}t+\varphi )+\text{sin}({\omega }_{f}t+\varphi )\right)}$

Tenemos la composición de dos MAS de frecuencias casi iguales ω₀ y ω_f, uno de amplitud variable exp(-γt) y el otro de amplitud constante 1.

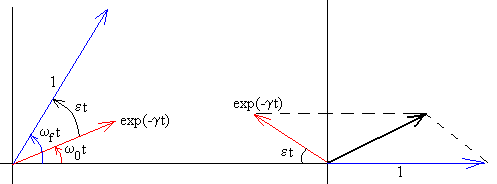
Mediante diagramas vectoriales podemos obtener el MAS resultante cuya frecuencia angular es aproximadamente ω₀, y cuya amplitud es la diagonal del paralelogramo de la figura de la derecha.

${\displaystyle x=\frac{F}{2m{\omega }_0\sqrt{{\epsilon }^2+{\gamma }^2}}\left(\sqrt{1-2\exp (-\gamma t)\cos (\epsilon t)+\exp (-2\gamma t)}\text{sin}({\omega }_{0}t+\varphi (t))\right)}$

la fase de la oscilación φ(t) varía lentamente con el tiempo. La amplitud, la raíz cuadrada que multiplica a la función seno, varía lentamente con la diferencia de frecuencias ε= ω_f-ω₀, alrededor del valor medio

${\displaystyle \frac{F}{2m{\omega }_0\sqrt{{\epsilon }^2+{\gamma }^2}}}$

La amplitud de la oscilación se acerca paulatinamente a este valor medio a medida que transcurre el tiempo tal como se puede ver en la figura. Durante el estado transitorio, la amplitud puede alcanzar valores de hasta casi dos veces la amplitud de las oscilaciones estables.

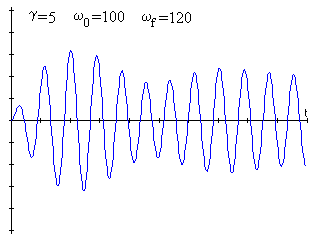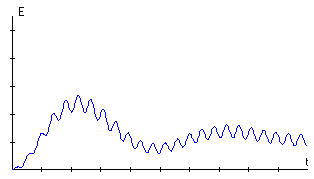En la figura de la derecha, se observa la energía total E del oscilador (suma de cinética y potencial) en función del tiempo. La representación gráfica nos sugiere que la energía del oscilador se describe mejor en términos de valores medios durante el periodo de una oscilación. El valor medio de la energía tiende hacia un valor constante cuando t se hace grande.

En la resonancia ω_f=ω₀

En la fórmula del desplazamiento x(t) se simplifica notablemente

${\displaystyle x=\frac{F}{2m\gamma {\omega }_0}\left(1-\exp (-\gamma t)\right)\text{sin}({\omega }_{0}t)}$

la amplitud crece lentamente, hasta que se acerca al valor asintótico, $\frac{F}{2m\gamma {\omega }_0}$ determinado por el coeficiente de rozamiento, tal como puede verse en la figura.

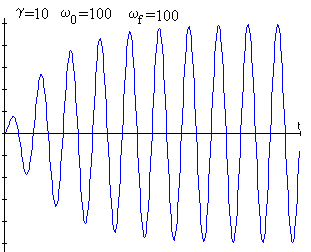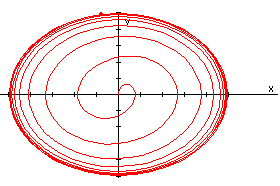En la figura de la derecha, observamos la representación del la trayectoria de la partícula en el espacio de las fases, el espacio x-v (posición-velocidad). La partícula sale del origen y describe una espiral que tiende hacia una elipse límite, que se alcanza en el estado estacionario.

Actividades

Se introduce

• la posición inicial x₀, en el control de edición titulado Posición
• la velocidad inicial del móvil v₀, en el control de edición titulado Velocidad.
• la constante de amortiguamiento γ, en el control de edición titulado Cte. amortiguamiento
• la amplitud F de la fuerza oscilante, en el control de edición titulado Amplitud
• La frecuencia angular ω_f de la fuerza oscilante, en el control de edición titulado Frecuencia
• la frecuencia angular natural del oscilador ω₀ =100 rad/s no se puede modificar

Se pulsa en el botón Empieza.

• Se observa la posición del móvil en función del tiempo en la parte izquierda de la ventana, gráfico x-t.
• La trayectoria del móvil en el espacio de las fases, gráfico v-x, en la parte superior derecha.
• La energía total del móvil en función del tiempo, gráfico E-t, en la parte inferior derecha.

Ejemplos de oscilaciones forzadas

La amplitud F de la fuerza oscilante nos permite variar la escala vertical de la representación gráfica. Si la posición x(t) crece más allá de los límites de la ventan del applet, se reduce el valor de la amplitud F en el control de edición correspondiente.

La frecuencia propia del oscilador en ω₀ =100 rad/s, no se puede cambiar, pero se puede variar la frecuencia de la fuerza oscilante ω_f alrededor de dicha frecuencia.

Observar y describir cada una de las representaciones

1. El movimiento de la partícula en el espacio ordinario (x-t)
2. La trayectoria de la partícula en el espacio de las fases
3. La energía del móvil en función del tiempo.

en las siguientes situaciones sugeridas como ejemplos orientativos. Posteriormente, observar y describir otras situaciones.

Dos opciones se presentan para el estudio completo de las oscilaciones forzadas.

1. Condiciones iniciales  fijadas de antemano en (x=0, v=0), el móvil se encuentra en el origen en el instante inicial.

2. Condiciones iniciales que puede seleccionar el usuario del programa. Se trata de comprobar que el estado transitorio depende de las condiciones iniciales, pero no el estado estacionario (el que describe el comportamiento del oscilador, después de un cierto tiempo, teóricamente infinito. En la práctica, un intervalo de tiempo tanto más pequeño cuanto mayor sea la constante de amortiguamiento).

Condiciones iniciales  fijadas de antemano en (x=0, v=0),

1. Cerca de la resonancia  ω_f =110 y 90
2. En la resonancia  ω_f =100
3. Observar pulsos, para ω_f =80 y γ =1.

Condiciones iniciales fijadas por el usuario

• Con rozamiento (γ =10)

Ejemplos de condiciones iniciales en la resonancia (ω_f =100)

• x=-5, v=0
• x=+5, v=0
• x=0, v=+500
• x=0, v=-500

Ejemplos de condiciones iniciales en las proximidades de la resonancia (ω_f =90)

• x=-5, v=0
• x=+5, v=0
• x=0, v=+500
• x=0, v=-500

• Sin rozamiento (γ =0)

Ejemplos de condiciones iniciales en la resonancia (ω_f =100)

• x=1.5, v=0
• x=0, v=-50
• x=0, v=150

Ejemplos de condiciones iniciales en las proximidades de la resonancia (ω_f =90)

• x=5, v=0
• x=0, v=-10

ForzadasApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Kotkin G. L., Serbo V. G. Problemas de Mecánica clásica. Editorial Mir 1980, problema 5.11, págs. 30, 159-161

Curso Interactivo de Física en Internet © Ángel Franco García