• Inicio
• Oscilaciones
• Osciladores lineales

El péndulo giratorio de Pohl

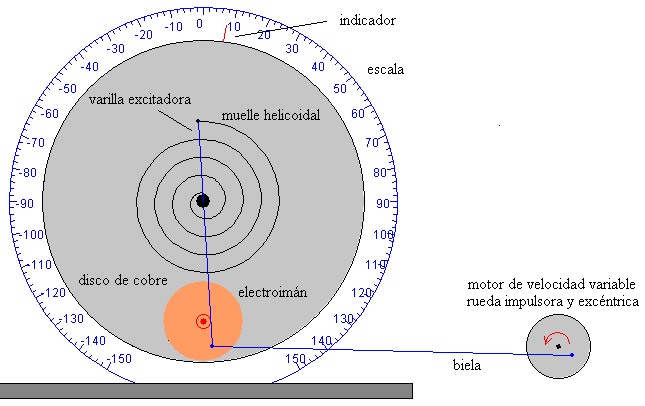
El péndulo de Pohl es un sistema oscilante que consta de un anillo de cobre unido a un muelle helicoidal que puede girar alrededor de un eje horizontal.

El disco se frena mediante las corrientes de Foucault que genera el campo magnético producido por una bobina en el anillo de cobre. Como se estudia en la página titulada “Corrientes de Foucault (I)” el momento de las fuerzas que ejerce el campo magnético sobre las corrientes inducidas es proporcional a la velocidad angular de rotación y de sentido contrario a ésta.

La intensidad del campo magnético es proporcional a la corriente i que pasa por la bobina, la fuerza sobre dichas corrientes es también proporcional al campo magnético. El momento de frenado es proporcional, por tanto, al cuadrado de la intensidad de la corriente que pasa por la bobina.

La fuerza oscilante se proporciona mediante un motor de velocidad variable, que dispone de una rueda impulsora y una excéntrica unida a una biela. La biela se atornilla a una varilla que puede girar alrededor del mismo eje y cuyo extremo está unido al muelle helicoidal. La varilla dispone de una ranura que permite ajustar la amplitud de la oscilación forzada. La varilla impulsora y el disco giran independientemente uno del otro, solamente están conectados por el muelle helicoidal.

En esta página, vamos a realizar dos experiencias simuladas con el péndulo giratorio de Pohl:

• Oscilaciones amortiguadas: medida de la constante de amortiguamiento

• Oscilaciones forzadas: medida de la amplitud en el estado estacionario en función de la frecuencia de la fuerza oscilante.

Oscilaciones amortiguadas

Se desplaza el disco de la posición de equilibrio y se suelta

La ecuación de la dinámica de rotación del anillo de cobre es

Iα=-kθ- λω

• α  es la aceleración angular del disco cuando el indicador del péndulo se encuentra en la posición angular θ.

• I es el momento de inercia del anillo respecto del eje de rotación

• k es la constante del muelle helicoidal

• λω es el momento de rozamiento proporcional a la velocidad angular ω de rotación, debidos a las corrientes de Foucault producidas en el disco de cobre por el campo magnético de la bobina.

Expresamos la ecuación del movimiento en forma de ecuación diferencial

${\displaystyle \frac{d^2\theta }{d{t}^2}+2\gamma \frac{d\theta }{dt}+{\omega }_0^2\theta =0{\omega }_{\text{0}}^{\text{2}}=\frac{k}{I}2\gamma =\frac{\lambda }{I}}$

ω₀ es la frecuencia natural o propia del oscilador, y γ es la constante de amortiguamiento.

El péndulo de Pohl de la marca Leybold-Heraeus que disponemos en el laboratorio de Física de la EUITI de Eibar tiene una frecuencia de aproximadamente f₀=0.5 Hz, un periodo P₀=1/f₀=2 s, la frecuencia angular propia es ω₀=2πf₀=π rad/s en ausencia de rozamiento, es decir, cuando no se conecta la bobina a la fuente de alimentación de corriente continua.

Oscilación es amortiguada. γ<ω₀

La solución de la ecuación diferencial es

${\displaystyle \theta =A\exp (-\gamma t)\text{sin}(\omega t+\varphi ){\omega }^2={\omega }_0^2-{\gamma }^2}$

ω es la frecuencia angular de la oscilación amortiguada, que difiere poco de la frecuencia propia ω₀, si el amortiguamiento γ es pequeño. No se debe de confundir ω la frecuencia de la oscilación amortiguada, con la velocidad angular de rotación del disco.

La velocidad angular de rotación dθ/dt es

${\displaystyle \frac{d\theta }{dt}=-\gamma A\exp (-\gamma t)\text{sin}(\omega t+\varphi )+A\exp (-\gamma t)\omega \cos (\omega t+\varphi )}$

Las condiciones iniciales determinan los valores de las constantes A y φ.

En la experiencia simulada, se desplaza el disco de cobre 150º, θ₀=5π/6 de la posición de equilibrio y se suelta, momento en el que empieza a contar el tiempo t=0.

θ₀=Asinφ
0=-γAsinφ+ ωAcosφ

Despejamos del sistema de dos ecuaciones con dos incógnitas A y φ.

${\displaystyle \tan \varphi =\frac{\omega }{\gamma }A=\frac{{\theta }_0}{\text{sin}\varphi }}$

Las sucesivas posiciones de máximo desplazamiento angular, para las cuales la velocidad angular del disco es cero, se denominan posiciones de retorno y se calculan poniendo dθ/dt=0

tan(ωt+φ)=ω/γ

${\displaystyle t_n=\frac{\left(\arctan \left(\frac{\omega }{\gamma }\right)-\varphi +n\pi \right)}{\omega }n=\text{0}\text{, 1}\text{, 2}\text{, }\mathrm{...}}$

Si el móvil parte de la posición θ₀ con velocidad angular nula, tanφ=ω/γ, los sucesivos tiempos son:

${\displaystyle \begin{array}{l}{t}_n=\frac{n\pi }{\omega }\\ {\theta }_n=A\exp (-\gamma t_n)\text{sin(}n\pi +\varphi \text{)}={\left(-1\right)}^n\frac{{\theta }_{\text{0}}}{\text{sin}\varphi }\exp (-\gamma t_n)\text{sin(}\varphi \text{)}={\left(-1\right)}^n{\theta }_0\exp (-\gamma t_n)\end{array}}$

Medida de la constante de amortiguamiento

En el instante t_m=mπ/ω, el máximo desplazamiento del indicador del péndulo es

${\displaystyle {\theta }_m={(-1)}^m{\theta }_0\exp (-\gamma t_m)}$

El cociente

${\displaystyle \begin{array}{l}\frac{\left|{\theta }_m\right|}{\left|{\theta }_n\right|}=\frac{e^{-\gamma t_m}}{e^{-\gamma t_n}}=\exp \left(-\gamma (t_m-t_n)\right)\\ \gamma =\frac{\ln \left|{\theta }_n\right|-\ln \left|{\theta }_m\right|}{t_m-t_n}\end{array}}$

Ejemplo. En el instante t=0, la posición de máximo desplazamiento es la posición inicial θ₀=150º, en el instante t₉=9.0 el desplazamiento máximo medido es -48.4º.

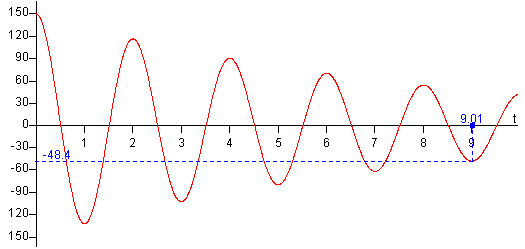
La constante de amortiguamiento γ vale

${\displaystyle \gamma =\frac{\ln 150-\ln 48.4}{9-0}=0.126}$

Comprobación

${\displaystyle \omega =\sqrt{{\omega }_0^2-{\gamma }^2}=3.139\text{rad/s}}$

t₉=9·π/ω=9.007 s

${\displaystyle {\theta }_9={(-1)}^9{\theta }_0\exp (-\gamma t_9)=-\frac{5\pi }{6}\exp (-0.126·9.007)=-0.844\text{rad}=-48.36º}$

Oscilación es crítica. γ=ω₀

La solución de la ecuación diferencial es

${\displaystyle \theta =(At+B)\exp (-\gamma t)}$

La velocidad angular de rotación dθ/dt es

${\displaystyle \frac{d\theta }{dt}=A\exp (-\gamma t)+(At+B)(-\gamma )\exp (-\gamma t)}$

Las condiciones iniciales determinan los valores de las constantes A y B.

En la experiencia simulada, se desplaza el disco de cobre 150º, θ₀=5π/6 de la posición de equilibrio y se suelta, momento en el que empieza a contar el tiempo t=0.

θ₀=B
0=A-γB

Despejamos del sistema de dos ecuaciones con dos incógnitas A y B.

${\displaystyle \theta ={\theta }_0(\gamma t+1)\exp (-\gamma t)}$

El oscilador tiende a la posición de equilibrio θ=0, después de un tiempo t→∞, sin oscilar

Oscilación es sobreamortiguada. γ>ω₀

La solución de la ecuación diferencial es

${\displaystyle \theta =(A\exp (-\beta t)+B\exp (\beta t))\exp (-\gamma t){\beta }^2={\gamma }^2-{\omega }_0^2}$

La velocidad angular de rotación dθ/dt es

${\displaystyle \frac{d\theta }{dt}=\left(-\beta A\exp (-\beta t)+\beta B\exp (\beta t)\right)\exp (-\gamma t)+\left(A\exp (-\beta t)+B\exp (\beta t)\right)(-\gamma )\exp (-\gamma t)}$

Las condiciones iniciales determinan los valores de las constantes A y B.

En la experiencia simulada, se desplaza el disco de cobre 150º, θ₀=5π/6 de la posición de equilibrio y se suelta, momento en el que empieza a contar el tiempo t=0.

θ₀=A+B
0=β(B-A)-γ(A+B)

Despejamos del sistema de dos ecuaciones con dos incógnitas A y B.

${\displaystyle \theta =\frac{{\theta }_0}{2}\left\{\left(1-\frac{\gamma }{\beta }\right)\exp (-\beta t)+\left(1+\frac{\gamma }{\beta }\right)\exp (\beta t)\right\}\exp (-\gamma t)}$

El oscilador tiende a la posición de equilibrio θ=0, después de un tiempo t→∞, sin oscilar.

Actividades

Se introduce,

• La intensidad i de la corriente que pasa por la bobina, lo que equivale a una constante de amortiguamiento γ=1.396·i²

• La frecuencia propia o natural del oscilador se mantiene fija e igual a ω₀=π rad/s

Se pulsa el botón titulado Empieza

Se observa las oscilaciones amortiguadas del péndulo de Pohl

Se pulsa el botón titulado Gráfica

Se representa 5 periodos de la oscilación amortiguada.

Arrastramos con el puntero del ratón el punto de color azul situado en el eje horizontal y medimos dos posiciones de desplazamiento máximo, θ_n y θ_m alejadas una de la otra, y los correspondientes tiempos t_n y t_m. Calculamos la constante de amortiguamiento γ, mediante la fórmula

${\displaystyle \gamma =\frac{\ln \left|{\theta }_n\right|-\ln \left|{\theta }_m\right|}{t_m-t_n}}$

AmortiguadasApplet aparecerá en un explorador compatible con JDK 1.1.

Se pulsa el botón titulado Gráfica. Se arrastra con el puntero del ratón el punto de color azul situado en  el eje horizontal

Curso Interactivo de Física en Internet © Ángel Franco García