M.A.S y movimiento circular uniforme
En esta página, vamos a interpretar geométricamente el Movimiento Armónico Simple (M. A. S.), relacionándolo con el movimiento circular uniforme.
MAS y movimiento circular
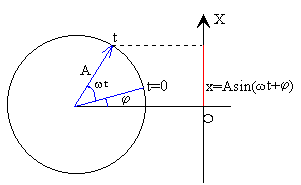La ecuación de un
M.A.S. es
x=A·sin(ωt+φ)
En la figura, se observa la interpretación de un M.A.S. como proyección sobre el eje X, del extremo de un vector rotatorio de longitud igual a la amplitud A, que gira con velocidad angular ω igual a la frecuencia angular del M.A.S, en el sentido contrario a las agujas del reloj.
El ángulo ω t+φ que forma el vector rotatorio con el eje de las X se denomina fase del movimiento. El ángulo φ que forma en el instante t=0, se denomina fase inicial.
Actividades
Se introduce
- la amplitud A, en el control de edición titulado Amplitud
- la frecuencia angular ω, en el control de edición titulado Frecuencia angular
- la fase inicial φ (en grados), en el control de edición titulado Fase inicial
Se pulsa en el botón titulado Empieza,
Para practicar con el programa interactivo, se sugiere probar los siguientes ejemplos:
| Amplitud | Frecuencia | Fase inicial |
| 2 | 1 | 0 |
| 2 | 1 | 90 |
| 2 | 1 | 180 |
| 2 | 1 | 270 |
| 2 | 2 | 0 |
| 1 | ||