La aceleración en un M.A.S.

En esta página, vamos a resolver un problema que pone de manifiesto el valor y dirección de la aceleración en un MAS

Una plataforma describe un MAS de amplitud A y frecuencia angular ω. Sobre la plataforma descansa una bolita de masa m. Calcular la posición x₀ y el instante t₀ en el que la bolita se despega de la plataforma.

Movimiento Armónico Simple

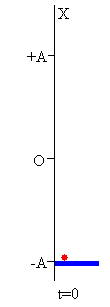
La plataforma describe un MAS de frecuencia ω angular. En el instante t=0 parte del reposo desde la posición x=-A, siendo A la amplitud de la oscilación

$\begin{array}{l} x = A \sin (ω t + ϕ) \\ v = \frac{d x}{d t} = A ω \cos (ω t + ϕ) \end{array}$

en el instante t=0, la posición y velocidad inicial son, respectivamente,

-A=Asinφ
0=Aωcosφ

De las condiciones iniciales, despejamos la fase inicial φ=-π/2

La ecuación del MAS se escribe

x=A·sin(ωt-π/2)=-A·cos (ωt)

Derivando con respecto al tiempo obtenemos las expresiones de la velocidad y aceleración.

v=A·ωsin (ωt)

a=A·ω²cos(ωt)=- ω²x

Fuerzas sobre la bolita

Cuando la plataforma se encuentra en la posición x las fuerzas sobre la bolita que descansa en la plataforma son

El peso, mg
La reacción o fuerza que ejerce la plataforma, N

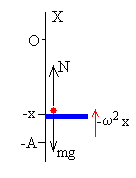Cuando la plataforma está por debajo del origen x<0, la aceleración a es positiva

La segunda ley de Newton se escribe

N-mg=-mω²x
N=mg-mω²x

Como x<0 la reacción N es siempre mayor que el peso

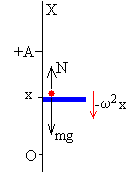Cuando la plataforma está por encima del origen x>0, la aceleración a es negativa

La segunda ley de Newton se escribe

N-mg=-mω²x
N=mg-mω²x

Como x>0 la reacción N es siempre menor que el peso

La máxima aceleración se produce cuando la plataforma alcanza el punto de retorno x=A. La bolita permanecerá sobre la plataforma siempre que N>0, es decir siempre que

mg> mω²A o bien, que g>ω²A

Cuando N se hace cero la bolita deja de estar en contacto con la plataforma, esto se produce en la posición x₀>0 tal que

g=ω²x₀

En el instante t₀ tal que

$\frac{g}{ω^{2}} = - A \cos (ω t_{0})$

La velocidad de la plataforma y la inicial de la bolita son

v₀=A·ωsin (ωt₀)

La bolita se mueva baja la acción de la aceleración constante de la gravedad.

$y = x_{0} + v_{0} (t - t_{0}) - \frac{1}{2} g {(t - t_{0})}^{2}$

La bolita chocará repetidamente con la plataforma, pero esta situación más avanzado se estudia en la página titulada "Una bola que cae y rebota sobre un pistón que oscila verticalmente"

Ejemplo.

Sea la amplitud A=0.1, la bolita se desprende de la plataforma si la frecuencia angular ω es mayor que ω_c o el periodo P<P_c.

$\begin{array}{l} ω_{c} = \sqrt{\frac{g}{A}} ω_{c} = \sqrt{\frac{9.8}{0.1}} = 9.90 rad/s \\ P_{c} = \frac{2 π}{ω_{c}} = 0.63 s \end{array}$

Si el periodo P=0.45 s, la frecuencia angular es ω=13.96 rad/s

La bolita se desprende en la posición x₀=0.05 m

En el instante t₀, tal que

x₀=-0.1cos (ωt₀), t₀=0.15 s

La velocidad inicial de la bolita en dicho instante es

v₀=0.1ωsin (ωt₀)=1.21 m/s

Actividades

Se introduce

El periodo del MAS que describe la plataforma, actuando en la barra de desplazamiento titulada Periodo.
La amplitud del MAS de la plataforma se ha fijado en A=0.1 m

Se pulsa el botón titulado Empieza

Observamos el movimiento de la bolita sobre la plataforma. A la derecha del applet, la gráfica de la posición de la bolita (en color rojo) y de la plataforma (en color azul) en función del tiempo.

A la izquierda, las fuerzas sobre la bolita

El peso, mg
La reacción de la plataforma, N

Cuando la fuerza que ejerce la plataforma N se hace cero, la bolita despega de la plataforma.