Conservación del momento lineal y del momento angular en una colisión

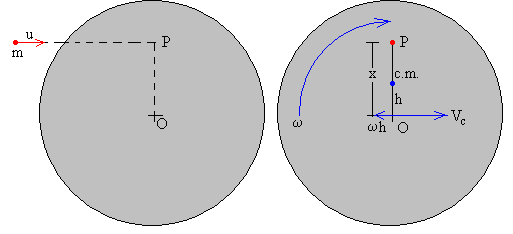
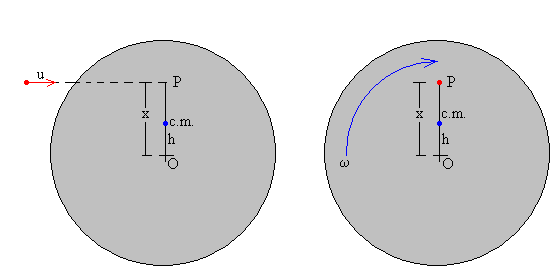
Se coloca un disco de masa M y radio R en una mesa de aire. Se dispara un proyectil con una pistola de aire comprimido que queda alojado en el disco a una distancia x de su centro. El centro de masas del sistema formado por el disco y la bala (punto de color azul) se mueve con velocidad V_c. El sistema, además gira con velocidad angular ω alrededor de un eje perpendicular al plano del disco que pasa el c.m..

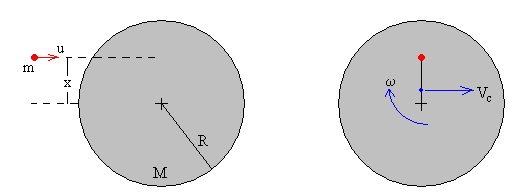
El sistema formado por la bala y el disco es aislado, la resultante de las fuerzas exteriores es cero, por lo que se verifica simultáneamente el principios de conservación del momento lineal y del momento angular.

Principio de conservación del momento lineal.

$F_{e x t} = \frac{d P}{d t} F_{e x t} = 0 P = cte$

Si la masa de la bala es m y su velocidad es u y el disco de masa M está inicialmente en reposo.

mu=(M+m)V_c

Donde V_c es la velocidad del centro de masas que ahora no coincide con el centro del disco, sino que está situado a una distancia h de su centro

$h = \frac{m}{M + m} x$

Principio de conservación del momento angular

$M_{e x t} = \frac{d L}{d t} M_{e x t} = 0 L = cte$

Calculamos el momento angular respecto del punto P de impacto de la bala.

El momento angular inicial es cero

El momento angular final es la suma del momento angular debido al movimiento de rotación del disco alrededor de une eje que pasa por su centro O y del momento angular orbital de O alrededor del punto P.

La velocidad de O es la suma de la velocidad del c.m. V_c y la velocidad de rotación alrededor de un eje que pasa por el c.m. ω×h

El momento angular disco respecto al punto P es

-I_oω+Mx(V_c-ωh)=0

Donde el momento de inercia del disco es I_o=MR²/2

Despejamos la velocidad del c.m. V_c de la primera ecuación y la velocidad angular de rotación ω de la segunda.

$V_{c} = \frac{m}{M + m} u ω = \frac{m x}{I_{o} (1 + \frac{m}{M}) + m x^{2}} u$

Otra alternativa, es la de calcular el momento angular respecto del centro de masas (c.m.).

El momento angular inicial es m(x-h)u

El momento angular final del sistema formado por el disco y la bala incrustada describiendo un movimiento de rotación alrededor de un eje que pasa por el c.m. es

$(I_{o} + M h^{2} + m {(x - h)}^{2}) ω$

I_o+Mh² es el momento de inercia del disco respecto de un eje que pasa por el c.m. (teorema de Steiner), el otro término es el momento de inercia de la bala.

Igualando el momento angular inicial al final, despejamos la velocidad angular de rotación

$\begin{array}{l} m (x - h) u = (I_{o} + M h^{2} + m {(x - h)}^{2}) ω \\ ω = \frac{m x}{I_{o} (1 + \frac{m}{M}) + m x^{2}} u \end{array}$

La energía perdida en la colisión Q es la diferencia entre las energías cinética final e inicial.

La energía inicial es la energía cinética de la bala.

La energía final es la suma de la energía cinética de traslación del sistema formado por el disco y la bala, y la energía cinética de rotación de dicho sistema alrededor de un eje que pasa por el c.m.

$\frac{1}{2} m u^{2} + Q = \frac{1}{2} (M + m) V_{c}^{2} + \frac{1}{2} (I_{o} + M h^{2} + m {(x - h)}^{2}) ω^{2}$

Ejemplo

Velocidad inicial de la bala u=1.0 m/s
Masa de la bala m=0.5 kg
Masa del disco M=1.5 kg
Radio del disco R=0.5 m
Parámetro de impacto de la bala x=0.3

El momento de inercia del disco respecto de un eje perpendicular al disco que pasa por su centro es

$I_{o} = \frac{1}{2} M R^{2} = \frac{1}{2} 1.5 \cdot {0.5}^{2} = 0.1875 {kgm}^{2}$

La posición h del centro de masas del sistema formado por el disco y la bala medido desde el centro del disco es

$h = \frac{m}{M + m} x = \frac{0.5}{1.5 + 0.5} 0.3 = 0.075 m$

La velocidad del c.m. V_c y la velocidad angular de rotación ω del sistema formado por el disco y la bala respecto de un eje que pasa por el c.m. valen, respectivamente,

$\begin{array}{l} V_{c} = \frac{m}{M + m} u = \frac{0.5}{1.5 + 0.5} 1.0 = 0.25 m/s \\ ω = \frac{m x}{I_{o} (1 + \frac{m}{M}) + m x^{2}} u = \frac{0.5 \cdot 0.3}{0.1875 (1 + \frac{0.5}{1.5}) + 0.5 \cdot {0.3}^{2}} 1.0 = 0.508 rad/s \end{array}$

Balance energético de la colisión

$\begin{array}{l} \frac{1}{2} m u^{2} + Q = \frac{1}{2} (M + m) V_{c}^{2} + \frac{1}{2} (I_{o} + M h^{2} + m {(x - h)}^{2}) ω^{2} \\ \frac{1}{2} 0.5 \cdot {1.0}^{2} + Q = \frac{1}{2} (1.5 + 0.5) \cdot {0.25}^{2} + \frac{1}{2} (0.1875 + 1.5 \cdot {0.075}^{2} + 0.5 \cdot {0.225}^{2}) {0.508}^{2} Q = - 0.159 J \end{array}$

Actividades

Se introduce

La masa m de la bala, en el control de edición titulado Masa bala.
La masa del disco M, en el control de edición titulado Masa disco
El radio del disco se mantiene fijo e igual a 0.5 m.
La velocidad u de la bala incidente se mantiene fija e igual a 1 m/s.

Se pulsa el botón titulado Nuevo

Con el puntero del ratón, se arrastra la bala de color rojo, para fijar el valor del parámetro de impacto x.

Se pulsa el botón titulado Empieza

La bala se mueve hacia el disco. Choca y se incrusta en el disco a una distancia x de su centro, observamos el movimiento del conjunto formado por el disco y la bala después del choque.

En la parte superior derecha, se nos proporciona los datos relativos a las velocidades

V_c de traslación del centro del disco
ω de rotación del disco alrededor de un eje que pasa por su centro

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Arrastre la partícula de color rojo con el puntero del ratón

Referencias

Rockefeller R. R. Conservation of angular and linear momentum on an air table. Am. J. Phys. 43 (11) November 1975, pp. 981-98.